高三数学一轮复习五层训练(新高考地区)第34练空间向量与立体几何(原卷版+解析)

这是一份高三数学一轮复习五层训练(新高考地区)第34练空间向量与立体几何(原卷版+解析)，共43页。试卷主要包含了课本变式练，考点分类练，最新模拟练，综合提升练，高考真题练等内容，欢迎下载使用。
一、课本变式练
1.（人A选择性必修一P9习题1.1T2变式）如图所示，在平行六面体中，M为与的交点，若，，，则（ ）
A．B．
C．D．
2.（人A选择性必修一P14练习T2变式）已知正四面体ABCD，M为BC中点，N为AD中点，则直线BN与直线DM所成角的余弦值为（ ）
A．B．C．D．
3. （人A选择性必修一P22习题1.3T8变式）如图在边长是2的正方体中，E，F分别为AB，的中点．
（1）求异面直线EF与所成角的大小．
（2）证明：平面．
4. （人A选择性必修一P41习题1.3T7变式）在直三棱柱中，底面是等腰直角三角形，，侧棱，D，E分别是与的中点，点E在平面ABD上的射影是的重心G，则点到平面ABD的距离为（ ）
A．B．C．D．
二、考点分类练
(一)空间向量的运算
5. 设平面的法向量为，平面的法向量为，若，则的值为（ ）
A．3B．4C．5D．6
6. 已知正六棱柱的底面边长为1，是正六棱柱内（不含表面）的一点，则的取值范围是（ ）
A．B．
C．D．
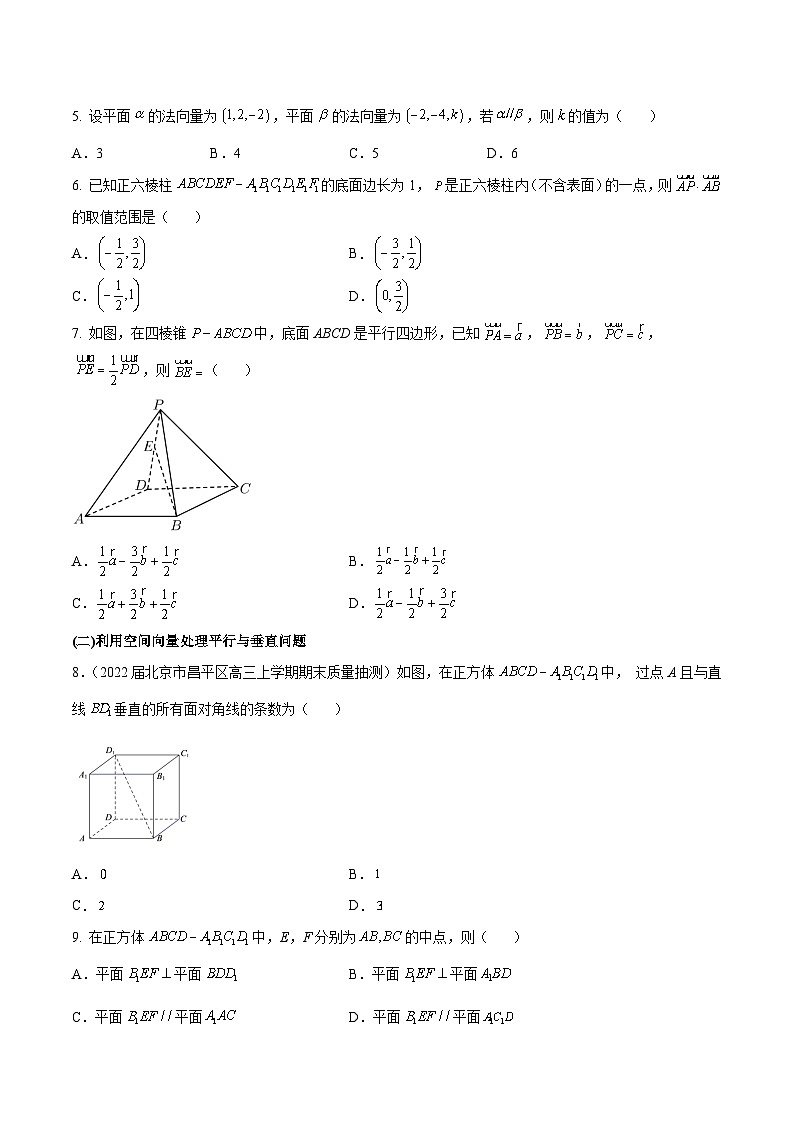
7. 如图，在四棱锥中，底面ABCD是平行四边形，已知，，，，则（ ）
A．B．
C．D．
(二)利用空间向量处理平行与垂直问题
8．（2022届北京市昌平区高三上学期期末质量抽测）如图，在正方体中， 过点A且与直线垂直的所有面对角线的条数为（ ）
A．B．
C．D．
9. 在正方体中，E，F分别为的中点，则（ ）
A．平面平面B．平面平面
C．平面平面D．平面平面
10. 如图，在直三棱柱中，，，D为AB的中点．试用向量的方法证明：平面．
(三)利用空间向量求空间角
11. 在正方体中O为面的中心，为面的中心.若E为中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
12. 已知正方体ABCD—的棱长为4，M在棱上，且1，则直线BM与平面所成角的正弦值为___________．
13. （2022届四川省成都市石室中学高三上学期联测）如图,在三棱锥中,是等边三角形,,点是 的中点,连接．
（1）证明:平面平面;
（2）若,且二面角为,求直线与平面所成角的正弦值．
14.（2023届云南省下关第一中学高三上学期见面考） 如图，已知AB为圆锥SO底面的直径，点C在圆锥底面的圆周上，，，BE平分，D是SC上一点，且平面平面SAB．
(1)求证：；
(2)求平面EBD与平面BDC所成角的余弦值．
(四)利用空间向量求距离
15. （2022届山西省长治市第二中学校高三下学期4月月考）在直四棱柱中，底面为正方形，．点P在侧面内，若平面，则点P到的距离的最小值为________．
16. （2022届北京市第五中学高三下学期三模）如图，在三棱柱 中，平面 平面 ，是矩形，已知 ，动点 在棱 上，点 在棱 上，且 .
(1)求证： ;
(2)若直线与平面所成角的正弦值为，求的值;
(3)在满足（2）的条件下，求点到平面的距离.
三、最新模拟练
17. （2023届广西桂林市高三上学期阶段性联合检测）如图，已知正方体ABCD-A1B1C1D1的中心为O，则下列结论中
①+与1+1是一对相反向量；
②-1与-1是一对相反向量；
③1+1+1+1与+++是一对相反向量；
④-与1-1是一对相反向量．
正确结论的个数为（ ）
A．1B．2C．3D．4
18. （2022届北京市海淀区首都师范大学附属中学高三下学期三模）如图，在正方体中，为棱上的动点，为棱的中点，则下列选项正确的是（ ）
A．直线与直线相交
B．当为棱上的中点时，则点在平面的射影是点
C．存在点，使得直线与直线所成角为
D．三棱锥的体积为定值
19. （2023届广东省七校联合体高三上学期第一次联考）如图，两个正方形ABCD和ADEF所在平面互相垂直，设M，N分别是AC和AE的中点，那么下列结论正确的是（ ）
A．B．平面
C．D．异面.
20. （2022届青海省高三第四次模拟）手工课可以提高学生的动手能力、反应能力、创造力，使学生在德、智、体、美、劳各方面得到全面发展，某小学生在一次手工课上制作了一座漂亮的房子模型，它可近似地看成是一个直三棱柱和一个长方体的组合图形，其直观图如图所示，，，P，Q，M，N分别是棱AB，，，的中点，则异面直线PQ与MN所成角的余弦值是______．
21. （2023届广东省深圳外国语学校高三上学期第一次月考）如图，在底面是菱形的四棱锥中，平面ABCD，，，点E，F分别为BC，PD的中点，设直线PC与平面AEF交于点Q.
(1)已知平面平面，求证：.
(2)求直线AQ与平面PCD所成角的正弦值.
22. （2022届天津市耀华中学高三下学期二模）如图，在四棱锥中，平面，底面是直角梯形，其中，，，，E为棱上的点，且.
(1)求证：平面；
(2)求二面角的余弦值；
(3)求点E到平面的距离.
24. （2022新高考全国卷Ⅰ）如图,直三棱柱的体积为4,的面积为．
（1）求A到平面的距离；
（2）设D为的中点,,平面平面,求二面角的正弦值．
25. （2022新高考全国卷2） 如图,是三棱锥的高,,,E是的中点．
（1）证明：平面；
（2）若,,,求二面角的正弦值．
26. （2021新高考全国卷2）在四棱锥中,底面是正方形,若
（1）求证：平面平面；
（2）求二面角的平面角的余弦值.
五、综合提升练
27. 如图，在正方体中，在棱上，，平行于的直线在正方形内，点到直线的距离记为，记二面角为为，已知初始状态下，，则（ ）
A．当增大时，先增大后减小B．当增大时，先减小后增大
C．当增大时，先增大后减小D．当增大时，先减小后增大
28. 在棱长为的正方体中，，分别为，的中点，点在正方体表面上运动，且满足，点轨迹的长度是___________.
29. 已知四棱锥的底面是平行四边形，平面与直线，，分别交于点，，且，点在直线上，为的中点，且直线平面.
（1）设，，，试用基底表示向量；
（2）证明，四面体中至少存在一个顶点从其出发的三条棱能够组成一个三角形；
（3）证明，对所有满足条件的平面，点都落在某一条长为的线段上.
30. 如图1，在△中，，分别为，的中点，为的中点，，．将△沿折起到△的位置，使得平面平面，如图2．
（1）求证：；
（2）求直线和平面所成角的正弦值；
（3）线段上是否存在点，使得直线和所成角的余弦值为？若存在，求出的值；若不存在，说明理由．
第34练 空间向量与立体几何
一、课本变式练
1.（人A选择性必修一P9习题1.1T2变式）如图所示，在平行六面体中，M为与的交点，若，，，则（ ）
A．B．
C．D．
【答案】D
【解析】由题意得，.故选D
2.（人A选择性必修一P14练习T2变式）已知正四面体ABCD，M为BC中点，N为AD中点，则直线BN与直线DM所成角的余弦值为（ ）
A．B．C．D．
【答案】B【解析】设该正面体的棱长为，因为M为BC中点，N为AD中点，
所以，
因为M为BC中点，N为AD中点，
所以有，
，
根据异面直线所成角的定义可知直线BN与直线DM所成角的余弦值为，故选B
3. （人A选择性必修一P22习题1.3T8变式）如图在边长是2的正方体中，E，F分别为AB，的中点．
（1）求异面直线EF与所成角的大小．
（2）证明：平面．
【解析】据题意，建立如图坐标系．于是：
，，，，，
∴，，，．
（1），
∴
∴异面直线EF和所成的角为．
（2）
∴，即
，
∴即．
又∵，平面且
∴平面．
4. （人A选择性必修一P41习题1.3T7变式）在直三棱柱中，底面是等腰直角三角形，，侧棱，D，E分别是与的中点，点E在平面ABD上的射影是的重心G，则点到平面ABD的距离为（ ）
A．B．C．D．
【答案】A
【解析】如图所示，以为坐标原点，，，所在直线分别为，，轴，建立空间直角坐标系，
设，则，0，，，，，，，0，，可得，，，，因为点在平面上的射影是的重心，所以平面，所以，
即，解得，即，则点到平面的距离为，是的中点，
所以．故选A.
二、考点分类练
(一)空间向量的运算
5. 设平面的法向量为，平面的法向量为，若，则的值为（ ）
A．3B．4C．5D．6
【答案】B
【解析】因为，所以，即，解得；故选B．
6. 已知正六棱柱的底面边长为1，是正六棱柱内（不含表面）的一点，则的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】建立如图所示的空间直角坐标系，且，
由正六边形的性质可得，，设，其中，
所以，，所以，所以的取值范围.故选A.
7. 如图，在四棱锥中，底面ABCD是平行四边形，已知，，，，则（ ）
A．B．
C．D．
【答案】A
【解析】连接BD，如图，
则
故选A．
(二)利用空间向量处理平行与垂直问题
8．（2022届北京市昌平区高三上学期期末质量抽测）如图，在正方体中， 过点A且与直线垂直的所有面对角线的条数为（ ）
A．B．
C．D．
【答案】C
【解析】过点A的面对角线一共有三条，AC，，，连接，AC，，，以为坐标原点，DA为x轴，DC为y轴，为z轴，建立空间直角坐标系，设正方体棱长为1，则，，，，，其中，，，，，，，故与垂直，与不垂直，故答案为2条. 故选C
9. 在正方体中，E，F分别为的中点，则（ ）
A．平面平面B．平面平面
C．平面平面D．平面平面
【解析】在正方体中，且平面，
又平面，所以，因为分别为的中点，
所以，所以，又，所以平面，
又平面，所以平面平面，故A正确；
如图，以点为原点，建立空间直角坐标系，设，
则，
，
则，，
设平面的法向量为，
则有，可取，
同理可得平面的法向量为，
平面的法向量为，
平面的法向量为，
则，
所以平面与平面不垂直，故B错误；
因为与不平行，
所以平面与平面不平行，故C错误；
因为与不平行，
所以平面与平面不平行，故D错误，故选A.
10. 如图，在直三棱柱中，，，D为AB的中点．试用向量的方法证明：平面．
【解析】证明：建立如图所示空间直角坐标系，设，
则，，
，
设平面的法向量为，
则，故可令，
则，
即，又平面,
所以平面.
(三)利用空间向量求空间角
11. 在正方体中O为面的中心，为面的中心.若E为中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】B
【解析】设正方体的边长为，建立如图所示空间直角坐标系，，
，设异面直线与所成角为，则.
故选B
12. 已知正方体ABCD—的棱长为4，M在棱上，且1，则直线BM与平面所成角的正弦值为___________．
【答案】
【解析】如图所示，以为原点，方向为轴，建立空间直角坐标系，
所以有，，，，，，
则，，，
设平面的法向量，则由
，令，得，
设直线BM与平面所成角为，则
，
13. （2022届四川省成都市石室中学高三上学期联测）如图,在三棱锥中,是等边三角形,,点是 的中点,连接．
（1）证明:平面平面;
（2）若,且二面角为,求直线与平面所成角的正弦值．
【解析】（1）证明:因为是等边三角形,,
所以,可得．
因为点是的中点,则,,
因为,平面PBD,平面,
所以平面,因为平面,
所以平面平面．
（2）如图,作,垂足为连接．
因为,
所以为二面角A-BD-C的平面角．
由已知二面角为,知．
在等腰三角形中,由余弦定理可得．
因为是等边三角形,则,所以．
在中,有,得,
因为,所以．
又,所以．
则,．
以为坐标原点,以向量的方向分别为轴,轴的正方向,
以过点垂直于平面的直线为轴,建立空间直角坐标系,
则,,向量,
平面的一个法向量为,
设直线与平面所成的角为,
则,
所以直线与平面所成角的正弦值为．
14.（2023届云南省下关第一中学高三上学期见面考） 如图，已知AB为圆锥SO底面的直径，点C在圆锥底面的圆周上，，，BE平分，D是SC上一点，且平面平面SAB．
(1)求证：；
(2)求平面EBD与平面BDC所成角的余弦值．
【解析】（1）因为，且BE平分，
所以，
又因为平面平面SAB，且平面平面，平面SAB，
所以平面BDE，
又因为平面BDE，
所以；
（2）取的中点M，连接OM，OS，则OM，OS，OA两两垂直，
所以以O为坐标原点，以OM为x轴，以OA为y轴，以OS为z轴建立如图空间直角坐标系，
则，，，，，
由（1）知平面BDE，所以是平面BDE的一个法向量，
设平面BDC的法向量为，
因为，
则，
取，则，
因此，
所以平面EBD与平面BDC所成角的余弦值为．
(四)利用空间向量求距离
15. （2022届山西省长治市第二中学校高三下学期4月月考）在直四棱柱中，底面为正方形，．点P在侧面内，若平面，则点P到的距离的最小值为________．
【答案】
【解析】建立如图所示空间直角坐标系，，，设，.由于平面，所以，所以.由于，即，到的距离为，
所以当时，.即到的距离的最小值为.
16. （2022届北京市第五中学高三下学期三模）如图，在三棱柱 中，平面 平面 ，是矩形，已知 ，动点 在棱 上，点 在棱 上，且 .
(1)求证： ;
(2)若直线与平面所成角的正弦值为，求的值;
(3)在满足（2）的条件下，求点到平面的距离.
【解析】 (1)因为四边形是矩形，所以，
又，，平面，
所以平面，又平面，
所以，
(2)因为平面平面 ，平面平面，
平面，，
所以平面，又，
所以两两相互垂直，以为原点，，，为，，轴的正方向建立空间直角坐标系，则，，，,
设，则，
所以，，
设平面的法向量为，，
则，，
取，可得，
设直线 与平面的夹角为，
则，
所以，
化简可得，又，
所以，所以；
(3)由(2) 平面的法向量为，，又，
设点到平面的距离为，
则.
所以点到平面的距离为.
三、最新模拟练
17. （2023届广西桂林市高三上学期阶段性联合检测）如图，已知正方体ABCD-A1B1C1D1的中心为O，则下列结论中
①+与1+1是一对相反向量；
②-1与-1是一对相反向量；
③1+1+1+1与+++是一对相反向量；
④-与1-1是一对相反向量．
正确结论的个数为（ ）
A．1B．2C．3D．4
【答案】A
【解析】设E,F分别为AD和A1D1的中点，
①+与+不是一对相反向量，错误；
②-与-不是一对相反向量，错误；
③1+1+1+是一对相反向量,正确；
④-与1-不是一对相反向量,是相等向量，错误．
即正确结论的个数为1个故选A
18. （2022届北京市海淀区首都师范大学附属中学高三下学期三模）如图，在正方体中，为棱上的动点，为棱的中点，则下列选项正确的是（ ）
A．直线与直线相交
B．当为棱上的中点时，则点在平面的射影是点
C．存在点，使得直线与直线所成角为
D．三棱锥的体积为定值
【答案】D
【解析】A：由题意知，，平面，平面
所以平面，
又平面，所以与不相交，故A错误；
B：连接，如图，
当点为的中点时，，又，所以，
若点在平面的射影为，则平面，垂足为，
所以，设正方体的棱长为2，则，
在中，，所以，
即不成立，故B错误；
C：建立如图空间直角坐标系，连接，则，
所以异面直线与所成角为直线与所成角，
设正方体的棱长为2，若存在点使得与所成角为，
则，所以，
所以，又，
得，解得，
不符合题意，故不存在点使得与所成角为，故C错误；
D：如图，
由等体积法可知，
又，
为定值，所以为定值，
所以三棱锥的体积为定值，故D正确.故选D.
19. （2023届广东省七校联合体高三上学期第一次联考）如图，两个正方形ABCD和ADEF所在平面互相垂直，设M，N分别是AC和AE的中点，那么下列结论正确的是（ ）
A．B．平面
C．D．异面.
【答案】ABC
【解析】由点为原点，分别以、、所在直线为轴、轴、轴，建立空间直角坐标系，设正方形ABCD和ADEF的边长为，如下图：
对于A选项，，，，，
则直线、的方向向量分别为，，
因为，所以，即，故A正确；
对于B选项，连接，如下图：
因为点分别为的中点，所以在中，，
因为平面，且平面，所以平面，故B正确；
由选项B可知，故C正确；故D错误；故选ABC.
20. （2022届青海省高三第四次模拟）手工课可以提高学生的动手能力、反应能力、创造力，使学生在德、智、体、美、劳各方面得到全面发展，某小学生在一次手工课上制作了一座漂亮的房子模型，它可近似地看成是一个直三棱柱和一个长方体的组合图形，其直观图如图所示，，，P，Q，M，N分别是棱AB，，，的中点，则异面直线PQ与MN所成角的余弦值是______．
【答案】
【解析】如图，以为原点建立空间直角坐标系，因为，，
所以可得，
所以，
所以，
所以异面直线PQ与MN所成角的余弦值是.
21. （2023届广东省深圳外国语学校高三上学期第一次月考）如图，在底面是菱形的四棱锥中，平面ABCD，，，点E，F分别为BC，PD的中点，设直线PC与平面AEF交于点Q.
(1)已知平面平面，求证：.
(2)求直线AQ与平面PCD所成角的正弦值.
【解析】（1）由已知，平面，平面，所以平面，
又平面，平面平面＝，
所以；
（2）由已知是正三角形，是中点，则，而，所以，又平面，
故以为轴建立空间直角坐标系，如图，
，则，，，，，则，
．，，．
设，则，
又共面，
所以存在实数，值得，
即，解得，
所以．
设平面的一个法向量是，
则，令，则，即，
设直线AQ与平面PCD所成角为，则
．
22. （2022届天津市耀华中学高三下学期二模）如图，在四棱锥中，平面，底面是直角梯形，其中，，，，E为棱上的点，且.
(1)求证：平面；
(2)求二面角的余弦值；
(3)求点E到平面的距离.
【解析】 (1)因为平面，平面，
所以，而，因此可以建立如下图所示的空间直角坐标系，
则有，
，，，
因为，
所以，而平面，
所以平面；
(2)设平面的法向量为，
，
则有，
由（1）可知平面的法向量为，
所以有，
由图知二面角为锐角，所以二面角的余弦值为；
(3)由（2）可知：平面的法向量为，
，所以可得：
，
所以点E到平面的距离为.
四、高考真题练
23.（2021新高考全国卷1）在正三棱柱中,,点满足,其中,,则（）
A. 当时,的周长为定值
B. 当时,三棱锥的体积为定值
C. 当时,有且仅有一个点,使得
D. 当时,有且仅有一个点,使得平面
【答案】BD
【解析】解法一：对于A,当时,,所以,因为,
所以点P是线段上的动点,所以周长不是定值,故A错误；
对于B,当时,,所以,因为,所以点为线段上的动点,而,平面,点到平面的距离为定值,所以,三棱锥的体积为定值,故B正确．
当时,,取中点M,中等N,则,即,
所以点点是线段MN上的动点,易得当点P与点M或点N重合时都有,故C错误；
对于D,当时,,取,中点为E,F．则,即,所以点是线段EF上的动点．若平面,则,取中点D,可得,
,所以平面,所以BD,所以点P与点F重合,D正确,故选BD.
解法二：易知,点在矩形内部（含边界）．
对于A,当时,,即此时线段,周长不是定值,故A错误；
对于B,当时,,故此时点轨迹为线段,而,平面,则有到平面的距离为定值,所以其体积为定值,故B正确．
对于C,当时,,取,中点分别为,,则,所以点轨迹为线段,不妨建系解决,建立空间直角坐标系如图,,,,则,,,所以或．故均满足,故C错误；
对于D,当时,,取,中点为．,所以点轨迹为线段．设,因为,所以,,所以,此时与重合,故D正确．故选BD．
24. （2022新高考全国卷Ⅰ）如图,直三棱柱的体积为4,的面积为．
（1）求A到平面的距离；
（2）设D为的中点,,平面平面,求二面角的正弦值．
【解析】（1）因为三棱柱的体积4,
所以,
在直三棱柱中,设点A到平面的距离为h,
由得,
所以,
所以点A到平面的距离为；
（2）如图,取的中点E,连接AE,因为,所以,
又平面平面,平面平面,
且平面,所以平面,
在直三棱柱中,平面,
由平面,平面可得,,
又平面且相交,所以平面,
所以两两垂直,以B为原点,直线分别为x轴,y轴,z轴,建立空间直角坐标系,
由（1）得,所以,,所以,
则,所以的中点,
则,,
设平面的一个法向量,则,
取,得,
设平面的一个法向量,则,取,
得,
则,
所以二面角的正弦值为.
25. （2022新高考全国卷2） 如图,是三棱锥的高,,,E是的中点．
（1）证明：平面；
（2）若,,,求二面角的正弦值．
【解析】（1）连接并延长交于点,连接、,
因为是三棱锥的高,所以平面,平面,
所以、,
又,所以,即,所以,
又,即,所以,,
所以
所以,即,所以为的中点,又为的中点,所以,
又平面,平面,
所以平面.
(2)如图,以点A为坐标原点,直线分别为x轴,y轴,过点A与平面ABC垂直的直线为z轴建立空间直角坐标系,
因为,,所以,
又,,所以,,
,所以,,,,所以,
则,,,
设平面的法向量为,则,
令,得；
设平面的法向量为,则,
取,得；
设二面角为,则=
所以,故二面角的正弦值为.
26. （2021新高考全国卷2）在四棱锥中,底面是正方形,若
（1）求证：平面平面；
（2）求二面角的平面角的余弦值.
【解析】(1)因为,
所以,所以,
因为底面是正方形,所以,
因为,所以,
因为,所以平面平面.
(2)在平面内，过作，交于，则，
结合（1）中的平面，故可建如图所示的空间坐标系.
则，故.
设平面的法向量，
则即，取，则，
故
而平面的法向量为，故.
二面角的平面角为锐角，故其余弦值为.
五、综合提升练
27. 如图，在正方体中，在棱上，，平行于的直线在正方形内，点到直线的距离记为，记二面角为为，已知初始状态下，，则（ ）
A．当增大时，先增大后减小B．当增大时，先减小后增大
C．当增大时，先增大后减小D．当增大时，先减小后增大
【答案】C
【解析】由题设，以为原点，为轴建立空间直角坐标系，
设正方体的棱长为2，则，，
设直线与交于，则，
则，，，
设平面的法向量为，
，，令，则
设平面的法向量为，又
，，令，则
利用空间向量夹角公式得
对于AB，令，则
显然函数在时为减函数，即减小，则增大，故AB 错误；
对于CD，当时，则
令，
求导
，令，得
故当时，，函数单减，即单减，增大；当时，，函数单增，即单增，减小；故当增大时，先增大后减小，故选C
28. 在棱长为的正方体中，，分别为，的中点，点在正方体表面上运动，且满足，点轨迹的长度是___________.
【答案】
【解析】在正方体中，以为坐标原点，分别以，，为轴，轴，轴建立空间直角坐标系，
∴，，，，∴，
设，则，
∵，∴，
当时，，当时，，
取，，，，
连结，，，，
则，，
∴四边形为矩形，则，，
即，，又和为平面中的两条相交直线，
∴平面，
又，，
∴为的中点，则平面，
为使，必有点平面，
又点在正方体表面上运动，所以点的轨迹为四边形，
又，，∴，则点的轨迹不是正方形，
则矩形的周长为.
29. 已知四棱锥的底面是平行四边形，平面与直线，，分别交于点，，且，点在直线上，为的中点，且直线平面.
（1）设，，，试用基底表示向量；
（2）证明，四面体中至少存在一个顶点从其出发的三条棱能够组成一个三角形；
（3）证明，对所有满足条件的平面，点都落在某一条长为的线段上.
【解析】（1）∵，而，
∴，
所以.
（2）不妨设是四面体最长的棱，则在，中，，，
∴，即，
故，至少有一个大于，不妨设，
∴，，构成三角形.
（3）设，，，由（1）知.
又，有，，，
∴，
，
，
设，又
∴
因为平面，所以存在实数，使得：，
∴
∴，消元：在有解.
当时，，即；
当时，，解得.
综上，有.
所以对所有满足条件的平面，点都落在某一条长为的线段上.
30. 如图1，在△中，，分别为，的中点，为的中点，，．将△沿折起到△的位置，使得平面平面，如图2．
（1）求证：；
（2）求直线和平面所成角的正弦值；
（3）线段上是否存在点，使得直线和所成角的余弦值为？若存在，求出的值；若不存在，说明理由．
【解析】（1）因为在△中，，分别为，的中点，
所以 ，．
所以，又为的中点，
所以 ．
因为平面平面，且平面，
所以 平面，
所以 ．
（2）取的中点，连接，所以．
由（1）得，．
如图建立空间直角坐标系．
由题意得，，，，．
所以，，．
设平面的法向量为，

则即
令，则，，所以．
设直线和平面所成的角为，
则．
所以 直线和平面所成角的正弦值为．
（3）线段上存在点适合题意．
设，其中．
设，则有，
所以，从而，
所以，又，
所以．
令，
整理得．
解得，舍去．
所以线段上存在点适合题意，且．