高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题15函数的基本性质单元测试(A)(原卷版+解析)

这是一份高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题15函数的基本性质单元测试(A)(原卷版+解析)，共17页。
第一章，第二章，函数的概念及其表示方法，函数的基本性质.
高考真题：
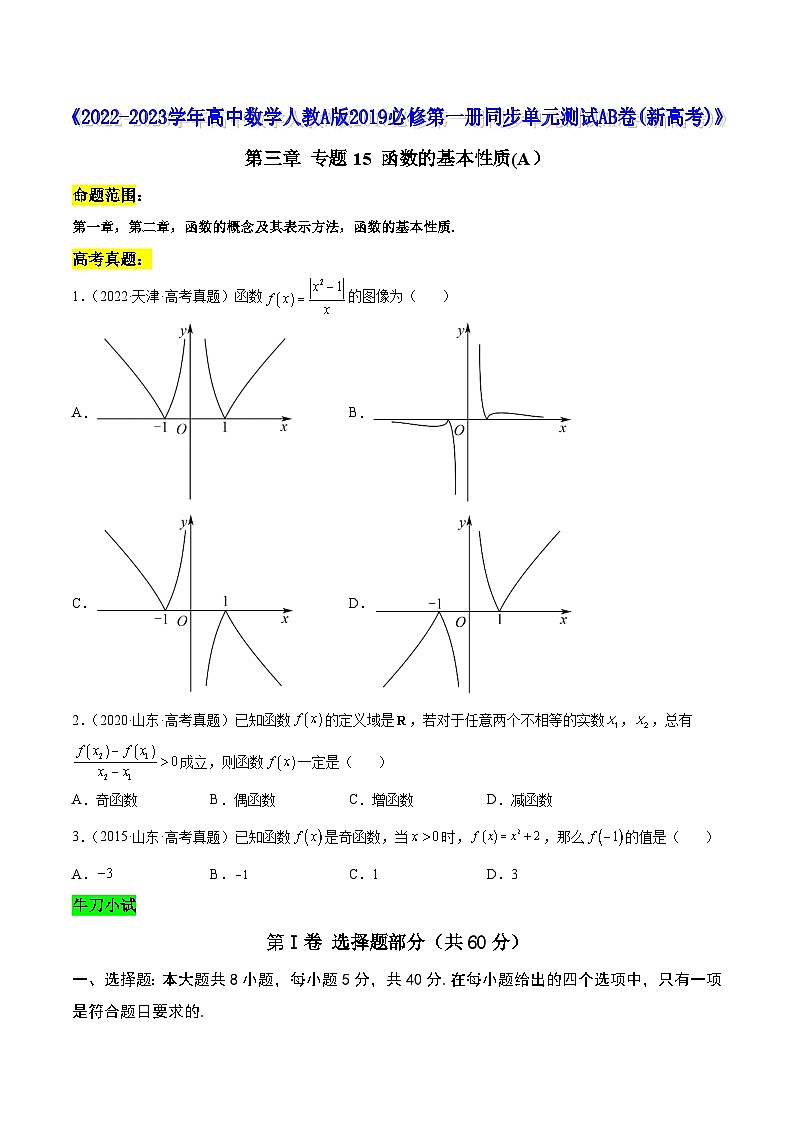
1．（2022·天津·高考真题）函数的图像为（ ）
A．B．
C．D．
2．（2020·山东·高考真题）已知函数的定义域是，若对于任意两个不相等的实数，，总有成立，则函数一定是（ ）
A．奇函数B．偶函数C．增函数D．减函数
3．（2015·山东·高考真题）已知函数是奇函数，当时，，那么的值是（ ）
A．B．C．1D．3
牛刀小试
第I卷 选择题部分（共60分）
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（2020·江苏镇江·高一期中）函数与函数的图象关于（ ）对称
A．轴B．轴C．坐标原点D．不能确定
2．（2022·全国·高一课时练习）下列命题正确的是（ ）
A．奇函数的图象关于原点对称，且
B．偶函数的图象关于y轴对称，且
C．存在既是奇函数又是偶函数的函数
D．奇､偶函数的定义域可以不关于原点对称
3．（2022·全国·高一课时练习）下列四个函数在是增函数的为（ ）
A．B．
C．D．
4．（2022·全国·高一课时练习）下列函数既是偶函数，又在上单调递增的是（ ）
A．B．C．D．
5．（2022·甘肃庆阳·高一期末）若函数在上单调递增，且，则实数的取值范围是（ ）
A．B．C．D．
6．（2022·全国·高一课时练习）设函数，则下列函数中为偶函数的是（ ）
A．B．
C．D．
7．（2022·广西桂林·高一期末）已知是以2为周期的函数，且，则（ ）
A．1B．-1C．D．7
8．（2022·全国·高一单元测试）已知函数是定义在上的奇函数，当时，，则( )
A．－12B．12C．9D．－9
二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得3分，有选错的得0分.
9．（2022·全国·高一课时练习）下列函数中，在上单调递增的是（ ）
A．B．C．D．
10．（2020·广东·新会陈经纶中学高一期中）下列哪个函数是其定义域上的偶函数（ ）
A．B．C．D．
11．（2022·全国·高一单元测试）关于函数，下列判断正确的是（ ）
A．在上单调递减B．在上单调递增
C．在上单调递减D．在上单调递增
12．（2021·广西·高一阶段练习）函数是定义在R上的奇函数，下列说法正确的有（ ）．
A．；
B．若在上有最小值，则在上有最大值3；
C．若在上为减函数，则在上是增函数.
D．
第II卷 非选择题部分（共90分）
三、填空题：本大题共4小题，每小题5分，共20分.
13．（2020·湖南·华容县教育科学研究室高一期末）已知函数为偶函数，则________
14．（2022·全国·高一课时练习）写出一个同时具有性质①对任意，都有；②的函数___________.
15．（2021·江苏省沭阳高级中学高一期中）已知函数是定义在上的奇函数，当时，，则__________.
16．（2022·全国·高一课时练习）函数的单调减区间为__________.
四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（2022·全国·高一课时练习）判断下列函数的奇偶性：
（1）；
（2）；
（3）；
（4）.
18．（2021·江苏·盐城市田家炳中学高一期中）已知函数．
(1)当时，判断函数的奇偶性；
(2)当时，判断函数在上的单调性，并证明．
19．（2021·四川自贡·高一期中）已知函数
(1)画出函数的图象；
(2)求的值；
(3)写出函数的单调递增区间.
20．（2022·重庆·巫山县官渡中学高一阶段练习）已知函数．
(1)证明函数为奇函数；
(2)若，求函数的最大值和最小值．
21．（2022·湖南·高一课时练习）已知二次函数的图象关于轴对称，且在区间上为增函数，试确定，，之间的大小关系．
22．（2020·黑龙江·哈尔滨市第一二二中学校高一期中）已知定义在的函数在单调递减，且.
(1)若是奇函数，求m的取值范围；
(2)若是偶函数，求m的取值范围.
第三章 专题15 函数的基本性质(A）
命题范围：
第一章，第二章，函数的概念及其表示方法，函数的基本性质.
高考真题：
1．（2022·天津·高考真题）函数的图像为（ ）
A．B．
C．D．
【答案】D
【分析】分析函数的定义域、奇偶性、单调性及其在上的函数值符号，结合排除法可得出合适的选项.
【详解】函数的定义域为，
且，
函数为奇函数，A选项错误；
又当时，，C选项错误；
当时，函数单调递增，故B选项错误；
故选：D.
2．（2020·山东·高考真题）已知函数的定义域是，若对于任意两个不相等的实数，，总有成立，则函数一定是（ ）
A．奇函数B．偶函数C．增函数D．减函数
【答案】C
【分析】利用函数单调性定义即可得到答案.
【详解】对于任意两个不相等的实数，，总有成立，
等价于对于任意两个不相等的实数，总有.
所以函数一定是增函数.
故选：C
3．（2015·山东·高考真题）已知函数是奇函数，当时，，那么的值是（ ）
A．B．C．1D．3
【答案】A
【分析】根据奇函数的性质即可求解.
【详解】函数是奇函数，当时，，
.
故选：A.
牛刀小试
第I卷 选择题部分（共60分）
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（2020·江苏镇江·高一期中）函数与函数的图象关于（ ）对称
A．轴B．轴C．坐标原点D．不能确定
【答案】B
【分析】由函数之间对称关系直接判断即可.
【详解】函数上的点关于轴对称点为，
点在函数上，与图象关于轴对称.
故选：B.
2．（2022·全国·高一课时练习）下列命题正确的是（ ）
A．奇函数的图象关于原点对称，且
B．偶函数的图象关于y轴对称，且
C．存在既是奇函数又是偶函数的函数
D．奇､偶函数的定义域可以不关于原点对称
【答案】C
【分析】根据奇偶性的定义判断．
【详解】奇函数的图象关于原点对称，但不一定在x=0时有意义，比如，A错误；
偶函数的图象关于y轴对称，但不一定等于0，如，B错误；
函数y=0既是奇函数又是偶函数，C正确；
奇､偶数的定义域均是关于原点对称的区间，D错误.
故选：C.
3．（2022·全国·高一课时练习）下列四个函数在是增函数的为（ ）
A．B．
C．D．
【答案】D
【分析】根据各个函数的性质逐个判断即可
【详解】对A，二次函数开口向上，对称轴为轴，在是减函数，故A不对．
对B，为一次函数，，在是减函数，故B不对．
对C，，二次函数，开口向下，对称轴为，在是增函数，故C不对．
对D，为反比例类型，，在是增函数，故D对．
故选：D
4．（2022·全国·高一课时练习）下列函数既是偶函数，又在上单调递增的是（ ）
A．B．C．D．
【答案】C
【分析】根据函数的奇偶性和单调性即可求解.
【详解】对于A，为奇函数，所以A不符合题意；
对于B，为偶函数，在上单调递减，所以B不符合题意；
对于C，既是偶函数，又在上单调递增，所以C符合题意；
对于D，为奇函数，所以D不符合题意．
故选：C．
5．（2022·甘肃庆阳·高一期末）若函数在上单调递增，且，则实数的取值范围是（ ）
A．B．C．D．
【答案】C
【分析】由单调性可直接得到，解不等式即可求得结果.
【详解】在上单调递增，，，解得：，
实数的取值范围为.
故选：C.
6．（2022·全国·高一课时练习）设函数，则下列函数中为偶函数的是（ ）
A．B．
C．D．
【答案】A
【分析】根据偶函数的定义即可判断.
【详解】，则，因为是偶函数，故为偶函数.
故选：A
7．（2022·广西桂林·高一期末）已知是以2为周期的函数，且，则（ ）
A．1B．-1C．D．7
【答案】A
【分析】除三角函数外，也有很多周期函数.可以利用周期函数的定义求值或求解析式.
【详解】因为函数是周期为2的周期函数，所以为的周期，即
所以.
故选：A.
8．（2022·全国·高一单元测试）已知函数是定义在上的奇函数，当时，，则( )
A．－12B．12C．9D．－9
【答案】B
【分析】先计算出，然后利用函数的奇偶性即可完成.
【详解】，因为函数是定义在上的奇函数，
所以，
故选：B.
二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得3分，有选错的得0分.
9．（2022·全国·高一课时练习）下列函数中，在上单调递增的是（ ）
A．B．C．D．
【答案】AD
【分析】画出各选项的函数图像，利用函数的图象来研究函数的单调性判断即可.
【详解】画出函数图象如图所示，
由图可得A，D中的函数在上单调递增，B，C中的函数在上不单调．
故选:AD．
10．（2020·广东·新会陈经纶中学高一期中）下列哪个函数是其定义域上的偶函数（ ）
A．B．C．D．
【答案】ABC
【分析】先求得函数定义域，根据偶函数的定义，逐一分析选项，即可得答案.
【详解】对于A：定义域为R，令，则，
所以为定义域上偶函数，故A正确；
对于B：定义域为R，令，则，
所以为定义域上偶函数，故B正确；
对于C：令，解得，定义域为，定义域关于原点对称，令，
则，
所以为定义域上偶函数，故C正确；
对于D：定义域为，不关于原点对称，故不是偶函数，故D错误.
故选：ABC
11．（2022·全国·高一单元测试）关于函数，下列判断正确的是（ ）
A．在上单调递减B．在上单调递增
C．在上单调递减D．在上单调递增
【答案】AC
【分析】由题可得，进而即得.
【详解】因为，
所以在和上单调递减，则A，C正确，B，D错误.
故选：AC.
12．（2021·广西·高一阶段练习）函数是定义在R上的奇函数，下列说法正确的有（ ）．
A．；
B．若在上有最小值，则在上有最大值3；
C．若在上为减函数，则在上是增函数.
D．
【答案】AB
【分析】依据奇函数性质判断选项ABD；举反例否定选项C.
【详解】选项A：函数是定义在R上的奇函数，则，则.判断正确；
选项B：奇函数的图像关于原点中心对称，故若在上有最小值，则在上有最大值3.判断正确；
选项C：奇函数在上为减函数，但在上依旧是减函数.判断错误；
选项D：函数是定义在R上的奇函数，则.判断错误.
故选：AB
第II卷 非选择题部分（共90分）
三、填空题：本大题共4小题，每小题5分，共20分.
13．（2020·湖南·华容县教育科学研究室高一期末）已知函数为偶函数，则________
【答案】
【分析】由偶函数的定义直接求解即可
【详解】因为函数为偶函数，
所以，即，
整理得，
因为
所以当时上式恒成立，
故答案为：0
14．（2022·全国·高一课时练习）写出一个同时具有性质①对任意，都有；②的函数___________.
【答案】（答案不唯一）
【分析】根据题意可得函数在为减函数，且再写出即可.
【详解】因为对任意，都有，所以函数在上减函数.又，故函数可以为.（注：满足题目条件的函数表达式均可.）
故答案为：（答案不唯一）
15．（2021·江苏省沭阳高级中学高一期中）已知函数是定义在上的奇函数，当时，，则__________.
【答案】3
【分析】根据奇函数的性质即可求解.
【详解】解：因为函数是定义在上的奇函数，故，
，故.
故答案为：3.
16．（2022·全国·高一课时练习）函数的单调减区间为__________.
【答案】##
【分析】优先考虑定义域，在研究复合函数的单调性时，要弄清楚它由什么函数复合而成的，再根据“同增异减”可求解.
【详解】函数是由函数和组成的复合函数，
，解得或，
函数的定义域是或，
因为函数在单调递减，在单调递增，
而在上单调递增，
由复合函数单调性的“同增异减”，可得函数的单调减区间．
故答案为：.
四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（2022·全国·高一课时练习）判断下列函数的奇偶性：
（1）；
（2）；
（3）；
（4）.
【答案】（1）奇函数
（2）既不是奇函数也不是偶函数
（3）既是奇函数又是偶函数
（4）奇函数
【分析】根据函数奇偶性的概念，逐问判断即可.
【详解】（1）由，得，且，
所以的定义域为，关于原点对称，
所以.
又，所以是奇函数.
（2）因为的定义域为，不关于原点对称，所以既不是奇函数也不是偶函数.
（3）对于函数，，其定义域为，关于原点对称.
因为对定义域内的每一个，都有，所以，，
所以既是奇函数又是偶函数.
（4）函数的定义域为，定义域关于原点对称.
①当时，，
所以，，所以；
②当时，，所以；
③当时，，所以.
综上，可知函数为奇函数.
18．（2021·江苏·盐城市田家炳中学高一期中）已知函数．
(1)当时，判断函数的奇偶性；
(2)当时，判断函数在上的单调性，并证明．
【答案】(1)奇函数
(2)在上是单调递减函数；证明见解析
【分析】(1)利用奇函数的定义判断即可；
（2）利用函数的单调性的定义即可判断与证明.
（1）
当时，，定义域为，关于原点对称，
，所以是奇函数．
（2）
当时，，证明：取，，
所以，，则，即，
所以在上是单调递减函数．
19．（2021·四川自贡·高一期中）已知函数
(1)画出函数的图象；
(2)求的值；
(3)写出函数的单调递增区间.
【答案】(1)图像见解析；
(2)；
(3)和.
【分析】(1)根据解析式分段描点连线即可；
(2)先计算，再计算即可；
(3)根据图像写出增区间即可.
(1)
(2)
；
(3)
由(1)得到的图像可知，f(x)的单调递增区间为和.
20．（2022·重庆·巫山县官渡中学高一阶段练习）已知函数．
(1)证明函数为奇函数；
(2)若，求函数的最大值和最小值．
【答案】(1)证明见解析
(2)最小值；最大值
【分析】（1）先判断函数定义域是否关于原点对称，再利用奇偶性的定义进行判断；
（2）先利用定义法判断函数的单调性，进而求出区间上的最值.
（1）
证明：的定义域为，关于原点对称，
，
所以在定义域上为奇函数；
（2）
（2）在上任取，且，
则
∵，
∴，，，
∴，
∴，
∴在上单调递增，
∴最小值为，最大值为
21．（2022·湖南·高一课时练习）已知二次函数的图象关于轴对称，且在区间上为增函数，试确定，，之间的大小关系．
【答案】
【分析】由二次函数的对称性可得函数的奇偶性，再根据函数的单调性比较各函数值大小.
【详解】由二次函数的图象关于轴对称，
可知函数为偶函数，
所以，
又函数在上为增函数，
所以，
即.
22．（2020·黑龙江·哈尔滨市第一二二中学校高一期中）已知定义在的函数在单调递减，且.
(1)若是奇函数，求m的取值范围；
(2)若是偶函数，求m的取值范围.
【答案】(1)
(2)
【分析】（1）根据奇函数，得到单调性，进而解不等式，求出答案；（2）根据偶函数，对不等式进行变形，进而得到不等式组，求出答案.
(1)
若是奇函数，则在上单调递减，故，解得：，故m的取值范围为；
(2)
若是偶函数，因为在上单调递减，故在上单调递增，由得：，故，解得：，
故m的取值范围为.