高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.6正、余弦定理及其应用举例(原卷版+解析)

这是一份高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.6正、余弦定理及其应用举例(原卷版+解析)，共48页。试卷主要包含了正、余弦定理，三角形常用面积公式等内容，欢迎下载使用。


知识点总结
1.正、余弦定理
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
2.在△ABC中，已知a，b和A时，解的情况如下：
3.三角形常用面积公式
(1)S＝eq \f(1,2)a·ha(ha表示a边上的高).
(2)S＝eq \f(1,2)absin C＝eq \f(1,2)acsin B＝eq \f(1,2)bcsin A＝eq \f(abc,4R).
(3)S＝eq \f(1,2)r(a＋b＋c)(r为内切圆半径).
[常用结论]
1.三角形中的三角函数关系
(1)sin(A＋B)＝sin C；
(2)cs(A＋B)＝－cs C；
(3)sineq \f(A＋B,2)＝cseq \f(C,2)；
(4)cseq \f(A＋B,2)＝sineq \f(C,2).
2.在△ABC中，两边之和大于第三边，两边之差小于第三边，A>B⇔a>b⇔sin A
>sin B⇔cs A典型例题分析
考向一 利用正、余弦定理解三角形
例1 (1)在△ABC中，角A，B，C所对的边分别为a，b，c，若a＝1，b＝eq \r(2)，A＝30°，则B等于( )
A.30° B.45°
C.30°或150° D.45°或135°
(2)(2021·全国甲卷)在△ABC中，已知B＝120°，AC＝eq \r(19)，AB＝2，则BC＝( )
A.1 B.eq \r(2)
C.eq \r(5) D.3
(3)(2023·广州模拟)在△ABC中，内角A，B，C所对的边分别为a，b，c，且满足2cs Bcs C·(tan B＋tan C)＝cs Btan B＋cs Ctan C，则cs A的最小值是________.
感悟提升 1.利用正弦定理可解决以下两类三角形问题：一是已知两角和一角的对边，求其他边与角；二是已知两边和一边的对角，求其他边与角(该三角形具有不唯一性，常根据三角函数值的有界性和大边对大角定理进行判断).
2.利用余弦定理可解决以下两类三角形问题：一是已知两边和它们的夹角，求其他边与角；二是已知三边求各个角.由于这两种情形下的三角形是唯一确定的，所以其解也是唯一的.
考向二 判断三角形的形状
例2 (1)在△ABC中，eq \f(c－a,2c)＝sin2eq \f(B,2)(a，b，c分别为角A，B，C的对边)，则△ABC的形状为( )
A.直角三角形B.等边三角形
C.等腰三角形或直角三角形D.等腰直角三角形
(2)在△ABC中，eq \f(sin A,sin B)＝eq \f(a,c)，(b＋c＋a)(b＋c－a)＝3bc，则△ABC的形状为________.
感悟提升 判断三角形形状的两种思路
(1)化为边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状.
(2)化为角：通过三角恒等变形，得出内角的关系，从而判断三角形的形状.此时要注意应用A＋B＋C＝π这个结论.
考向三 与三角形面积(周长)有关的计算
例3 (2022·新高考Ⅱ卷)记△ABC的内角A，B，C的对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为S1，S2，S3.已知S1－S2＋S3＝eq \f(\r(3),2)，sin B＝eq \f(1,3).
(1)求△ABC的面积；
(2)若sin Asin C＝eq \f(\r(2),3)，求b.
感悟提升 三角形面积公式的应用原则
(1)对于面积公式S＝eq \f(1,2)absin C＝eq \f(1,2)acsin B＝eq \f(1,2)bcsin A，一般是已知哪一个角就使用哪一个公式.
(2)与面积有关的问题，一般要用到正弦定理或余弦定理进行边和角的转化.
考向四 多边形中的解三角形问题
例4 (2023·烟台一模)如图，四边形ABCD中，AB2＋BC2＋AB·BC＝AC2.
(1)若AB＝3BC＝3，求△ABC的面积；
(2)若CD＝eq \r(3)BC，∠CAD＝30°，∠BCD＝120°，求∠ACB的值.
感悟提升 平面几何中解三角形问题的求解思路
(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；
(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果.
考向五 三角形中的最值、范围问题
例5(2022·新高考Ⅰ卷)记△ABC的内角A，B，C的对边分别为a，b，c，已知eq \f(cs A,1＋sin A)＝eq \f(sin 2B,1＋cs 2B).
(1)若C＝eq \f(2π,3)，求B；
(2)求eq \f(a2＋b2,c2)的最小值.
[思路分析] (1)化简条件式，利用C＝eq \f(2π,3)消去角A得到角B的三角方程，即可求解.
(2)利用条件式得到A，B的关系式，利用正弦定理把eq \f(a2＋b2,c2)转化为B的三角函数式，利用基本不等式求其最小值.
[规范解答] 解 (1)因为eq \f(cs A,1＋sin A)＝eq \f(sin 2B,1＋cs 2B)，
→eq \a\vs4\al(化倍角为单角以利于计算)
所以eq \f(cs A,1＋sin A)＝eq \f(sin B,cs B)，(2分)
所以cs Acs B＝sin B＋sin Asin B，
eq \x(所以cs（A＋B）＝sin B②)，(4分)
→由cs(A＋B)＝－cs C，角C＝eq \f(2π,3)，进而求B
所以sin B＝－cs C＝－cs eq \f(2π,3)＝eq \f(1,2).
→eq \a\vs4\al(利用B的范围求B)
(2)eq \x(由（1）得cs（A＋B）＝sin B，)
→eq \a\vs4\al(利用（1）题的结论)
所以sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－（A＋B）))＝sin B，
且0→eq \a\vs4\al(根据B与\f(π,2)－（A＋B）的范围确定其关系)
所以eq \f(π,2)－(A＋B)＝B，解得A＝eq \f(π,2)－2B，(8分)
→eq \a\vs4\al(利用正弦定理实现边角互化)
→eq \a\vs4\al(消去角A以利求解)
＝eq \f(cs22B＋sin2B,cs2B)＝eq \f(（2cs2B－1）2＋1－cs2B,cs2B)
→eq \a\vs4\al(化为基本不等式的形式)
≥2eq \r(4cs2B·\f(2,cs2B))－5＝4eq \r(2)－5③，
→eq \a\vs4\al(验证取等号的条件)
所以eq \f(a2＋b2,c2)的最小值为4eq \r(2)－5.(12分)
[满分规则]
❶得步骤分：
①处的实质都是解三角方程，都要注意写清楚角的范围，否则易失步骤分.
❷得关键分：
②处消去角A是本题得解的关键所在.
❸得计算分：
③处利用基本不等式求最小的关键是把目标函数化为其适用形式.
感悟提升 对于解三角形中的证明问题，要仔细观察条件与结论之间的联系，发现二者的差异，利用正弦定理、余弦定理及三角恒等变换把条件转换为结论，即为证明过程.
考向六 三角函数模型
例6 (多选)(2023·福州模拟)如图所示，一半径为4米的水轮，水轮圆心O距离水面2米，已知水轮每60秒逆时针转动一圈，如果当水轮上点P从水中浮现时(图中点P0)开始计时，则( )
A.点P第一次到达最高点需要20秒
B.当水轮转动155秒时，点P距离水面2米
C.当水轮转动50秒时，点P在水面下方，距离水面2米
D.点P距离水面的高度h(米)与t(秒)的函数解析式为h＝4cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t＋\f(π,3)))＋2
感悟提升 1.研究y＝Asin(ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题.
2.方程根的个数可转化为两个函数图象的交点个数.
3.三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，利用三角函数的有关知识解决问题.
基础题型训练
一、单选题
1．在中，已知，则（ ）
A．3B．2C．D．
2．有一拦水坝的横断面是等腰梯形,它的上底长为6m,下底长为10m,高为,那么此拦水坝斜坡的坡度和坡角分别为
A．B．C．D．
3．的内角A，B，C的对边分别为a，b，c．已知，，，则的面积为（ ）
A．B．C．D．
4．要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD＝120°，CD＝40 m，则电视塔的高度为（ ）
A．B．
C．D．
5．在中，，，，则满足条件的有（ ）
A．0个B．1个C．2个D．不确定
6．在锐角三角形中，，，分别是角，，的对边，已知，是方程的两个根，且，则c＝（ ）
A．4B．C．D．
二、多选题
7．某人在处向正东方向走后到达处，他沿南偏西方向走到达处，这时他离出发点，那么的值可以是（ ）
A．B．C．D．
8．的内角的对边分别为，下列结论一定成立的有（ ）
A．
B．若，则
C．若，则是等腰三角形
D．若，则是等腰三角形
三、填空题
9．在中，，，，则__________．
10．的内角、、所对边分别为、、，已知，则的最大值为__．
11．甲船在岛的正南处， ，甲船以每小时的速度向正北方向航行，同时乙船自出发以每小时的速度向北偏东的方向驶去，甲、乙两船相距最近的距离是_____.
12．在中，AB=1，BC=2，以C为直角顶点向外作等腰直角三角形ACD，当∠ABC变化时，线段BD的最大值为______．
四、解答题
13．在中，，，为边上一点，且．
（1）求；
（2）若，求．
14．在中，角所对的边分别为，且满足．
(1)求角的值；
(2)若，且，求的取值范围．
15．中，角A，B，C所对的边分别为a，b，c，，，．
(1)，时，求CD的长度；
(2)若CD为角C的平分线，且，求的面积．
16．已知的角，，的对边分别为，，，且．
(1)求的值；
(2)若，，求．
提升题型训练
一、单选题
1．在△ABC中，，则的值是（ ）
A．B．
C．D．
2．在中，角的对边分别为，若，则的值为（ ）
A．B．C．D．
3．已知的三个内角所对的边分别为，且满足，则（ ）
A．B．C．D．
4．在中，角的对边为，若，则当取最大值时，的面积是（ ）
A．B．C．D．
5．如图，四边形中，，，且、的周长相等，则（ ）
A．B．C．D．
6．如图为2022年北京冬奥会首钢滑雪大跳台示意图，为测量大跳台最高点距地面的距离，小明同学在场馆内的A点测得的仰角为，，，（单位：），（点在同一水平地面上），则大跳台最高高度（ ）
A．B．
C．D．
二、多选题
7．的内角､､的对边分别为､､，，，则可以为（ ）
A．7B．8C．9D．10
8．在中，角A，B，C的对边分别为a，b，c，且，则下列说法正确的有（ ）
A．
B．若，且的面积为，则的最小边长为2
C．若时，是唯一的，则
D．若时，周长的范围为
三、填空题
9．在中，已知，，，则边上的中线长为________．
10．在铺砌领域，有一座数学家们在半个多世纪里一直追寻的“圣杯”，这座圣杯名为“爱因斯坦”，指的是一个可以填满无限平面，且不会自我重复的“非周期性”铺砌块．2023年3月20日，一个由数学家和计算机科学家组成的研究团队，在论文预印网站arXiv上提交了一篇论文，表示他们找到了这样一种由多个相同的“风筝”粘在一起而形成的十三边形（如右图所示），只用此十三边形就能做到单铺砌块，也就是数学家们寻找的“圣杯”．若已知此十三边形最短的边长为1，则此十三边形的面积为_____________．
11．在中，内角，，的对边分别为，，若，且为的外心，为的重心，则的最小值为________．
12．在锐角三角形中，内角所对的边满足，若存在最大值，则实数的取值范围是__________．
四、解答题
13．在中，已知哪些条件可以应用余弦定理解三角形？
14．在中，内角所对的边分别为，.
（1）求；
（2）求.
15．在△中，角A，B，C的对边分别为a，b，c，且，是方程的两个实根.
(1)求和；
(2)若，求的值.
16．已知某渔船在渔港的南偏东方向，距离渔港约海里的处出现险情，此时在渔港的正上方恰好有一架海事巡逻飞机接到渔船的求救信号，海事巡逻飞机迅速将情况通知了在处的渔政船并要求其迅速赶往出事地点施救．若海事巡逻飞机测得渔船的俯角为，测得渔政船的俯角为，且渔政船位于渔船的北偏东方向上．
(1)计算渔政船与渔港的距离；
(2)若渔政船以每小时海里的速度直线行驶，能否在小时内赶到出事地点？
(参考数据：，，，，，）
定理
余弦定理
正弦定理
公式
a2＝b2＋c2－2bccs__A；
b2＝ ；
c2＝a2＋b2－2abcs__C
eq \f(a,sin A)＝ ＝ ＝2R
常见变形
cs A＝ ；
cs B＝
cs C＝eq \f(a2＋b2－c2,2ab)
(1)a＝2Rsin A，b＝ ，c＝ ；
(2)sin A＝eq \f(a,2R)，sin B＝ ，sin C＝eq \f(c,2R)；
(3)a∶b∶c＝ ；
(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin A
A为锐角
A为钝角或直角
图形
关系式
a＝bsin A
bsin Aa≥b
a>b
a≤b
解的个数
一解
所以eq \f(cs A,1＋sin A)＝eq \f(2sin Bcs B,1＋2cs2B－1)，
因为B∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,3)))eq \s\up12(①)，所以B＝eq \f(π,6).(5分)
所以0由正弦定理得eq \f(a2＋b2,c2)＝eq \f(sin2A＋sin2B,sin2C)
＝eq \f(sin2A＋sin2B,1－cs2C)＝eq \f(sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－2B))＋sin2B,1－sin2B)②
＝eq \f(4cs4B－5cs2B＋2,cs2B)＝4cs2B＋eq \f(2,cs2B)－5③(10分)
当且仅当cs2B＝eq \f(\r(2),2)时取等号，
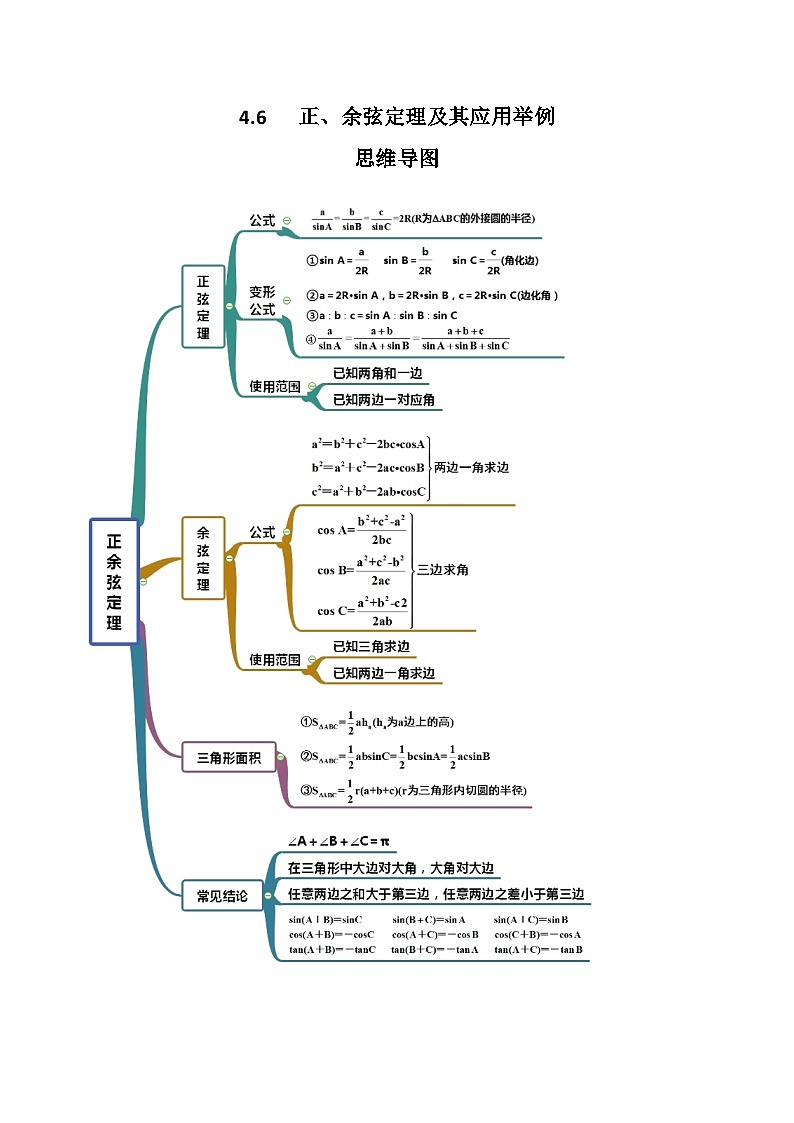
4.6 正、余弦定理及其应用举例
思维导图
知识点总结
1.正、余弦定理
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
2.在△ABC中，已知a，b和A时，解的情况如下：
3.三角形常用面积公式
(1)S＝eq \f(1,2)a·ha(ha表示a边上的高).
(2)S＝eq \f(1,2)absin C＝eq \f(1,2)acsin B＝eq \f(1,2)bcsin A＝eq \f(abc,4R).
(3)S＝eq \f(1,2)r(a＋b＋c)(r为内切圆半径).
[常用结论]
1.三角形中的三角函数关系
(1)sin(A＋B)＝sin C；
(2)cs(A＋B)＝－cs C；
(3)sineq \f(A＋B,2)＝cseq \f(C,2)；
(4)cseq \f(A＋B,2)＝sineq \f(C,2).
2.在△ABC中，两边之和大于第三边，两边之差小于第三边，A>B⇔a>b⇔sin A
>sin B⇔cs A典型例题分析
考向一 利用正、余弦定理解三角形
例1 (1)在△ABC中，角A，B，C所对的边分别为a，b，c，若a＝1，b＝eq \r(2)，A＝30°，则B等于( )
A.30° B.45°
C.30°或150° D.45°或135°
答案 D
解析 根据正弦定理eq \f(a,sin A)＝eq \f(b,sin B)，得sin B＝eq \f(bsin A,a)＝eq \f(\r(2)×\f(1,2),1)＝eq \f(\r(2),2).
由于b＝eq \r(2)＞1＝a，所以B＝45°或B＝135°.
(2)(2021·全国甲卷)在△ABC中，已知B＝120°，AC＝eq \r(19)，AB＝2，则BC＝( )
A.1 B.eq \r(2)
C.eq \r(5) D.3
答案 D
解析 法一 由余弦定理得AC2＝AB2＋BC2－2AB·BCcs B，
得BC2＋2BC－15＝0，
解得BC＝3或BC＝－5(舍去).
法二 由正弦定理eq \f(AC,sin B)＝eq \f(AB,sin C)，
得sin C＝eq \f(AB·sin B,AC)＝eq \f(\r(57),19)，
从而cs C＝eq \f(4\r(19),19)(C是锐角)，
所以sin A ＝sin [π－(B＋C)]＝sin(B＋C)＝sin Bcs C＋cs Bsin C
＝eq \f(\r(3),2)×eq \f(4\r(19),19)－eq \f(1,2)×eq \f(\r(57),19)＝eq \f(3\r(57),38).
又eq \f(AC,sin B)＝eq \f(BC,sin A)，所以BC＝eq \f(AC·sin A,sin B)＝3.
(3)(2023·广州模拟)在△ABC中，内角A，B，C所对的边分别为a，b，c，且满足2cs Bcs C·(tan B＋tan C)＝cs Btan B＋cs Ctan C，则cs A的最小值是________.
答案 eq \f(1,2)
解析 2cs Bcs C(tan B＋tan C)＝2cs Bcs Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(sin B,cs B)＋\f(sin C,cs C)))
＝2sin Bcs C＋2sin Ccs B＝2sin(B＋C)＝2sin A，
又cs Btan B＋cs Ctan C＝sin B＋sin C，
所以sin B＋sin C＝2sin A，
由正弦定理得b＋c＝2a，
由余弦定理，得
cs A＝eq \f(b2＋c2－a2,2bc)＝eq \f(b2＋c2－\b\lc\(\rc\)(\a\vs4\al\c1(\f(b＋c,2)))\s\up12(2),2bc)＝eq \f(3（b2＋c2）,8bc)－eq \f(1,4)≥eq \f(3bc,4bc)－eq \f(1,4)＝eq \f(1,2)，
当且仅当b＝c＝a时取等号，
故cs A的最小值为eq \f(1,2).
感悟提升 1.利用正弦定理可解决以下两类三角形问题：一是已知两角和一角的对边，求其他边与角；二是已知两边和一边的对角，求其他边与角(该三角形具有不唯一性，常根据三角函数值的有界性和大边对大角定理进行判断).
2.利用余弦定理可解决以下两类三角形问题：一是已知两边和它们的夹角，求其他边与角；二是已知三边求各个角.由于这两种情形下的三角形是唯一确定的，所以其解也是唯一的.
考向二 判断三角形的形状
例2 (1)在△ABC中，eq \f(c－a,2c)＝sin2eq \f(B,2)(a，b，c分别为角A，B，C的对边)，则△ABC的形状为( )
A.直角三角形B.等边三角形
C.等腰三角形或直角三角形D.等腰直角三角形
答案 A
解析 因为sin2 eq \f(B,2)＝eq \f(1－cs B,2)，
所以eq \f(c－a,2c)＝eq \f(1－cs B,2)，即cs B＝eq \f(a,c).
法一 由余弦定理得eq \f(a2＋c2－b2,2ac)＝eq \f(a,c)，
即a2＋c2－b2＝2a2，
所以a2＋b2＝c2.
所以△ABC为直角三角形，无法判断两直角边是否相等.
法二 由正弦定理得cs B＝eq \f(sin A,sin C)，
又sin A＝sin(B＋C)＝sin Bcs C＋cs Bsin C，
所以cs Bsin C＝sin Bcs C＋cs Bsin C，
即sin Bcs C＝0，
又sin B≠0，所以cs C＝0，
又角C为三角形的内角，所以C＝eq \f(π,2)，
所以△ABC为直角三角形，无法判断两直角边是否相等.
(2)在△ABC中，eq \f(sin A,sin B)＝eq \f(a,c)，(b＋c＋a)(b＋c－a)＝3bc，则△ABC的形状为________.
答案 等边三角形
解析 因为eq \f(sin A,sin B)＝eq \f(a,c)，所以eq \f(a,b)＝eq \f(a,c)，所以b＝c.
又(b＋c＋a)(b＋c－a)＝3bc，
所以b2＋c2－a2＝bc，
所以cs A＝eq \f(b2＋c2－a2,2bc)＝eq \f(bc,2bc)＝eq \f(1,2).
因为A∈(0，π)，所以A＝eq \f(π,3)，
所以△ABC是等边三角形.
感悟提升 判断三角形形状的两种思路
(1)化为边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状.
(2)化为角：通过三角恒等变形，得出内角的关系，从而判断三角形的形状.此时要注意应用A＋B＋C＝π这个结论.
考向三 与三角形面积(周长)有关的计算
例3 (2022·新高考Ⅱ卷)记△ABC的内角A，B，C的对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为S1，S2，S3.已知S1－S2＋S3＝eq \f(\r(3),2)，sin B＝eq \f(1,3).
(1)求△ABC的面积；
(2)若sin Asin C＝eq \f(\r(2),3)，求b.
解 (1)由S1－S2＋S3＝eq \f(\r(3),2)，
得eq \f(\r(3),4)(a2－b2＋c2)＝eq \f(\r(3),2)，
即a2－b2＋c2＝2，
又a2－b2＋c2＝2accs B，
所以accs B＝1.由sin B＝eq \f(1,3)，
得cs B＝eq \f(2\r(2),3)或cs B＝－eq \f(2\r(2),3)(舍去)，
所以ac＝eq \f(3,2\r(2))＝eq \f(3\r(2),4)，
则△ABC的面积S＝eq \f(1,2)acsin B＝eq \f(1,2)×eq \f(3\r(2),4)×eq \f(1,3)＝eq \f(\r(2),8).
(2)由sin Asin C＝eq \f(\r(2),3)，ac＝eq \f(3\r(2),4)及正弦定理知
eq \f(b2,sin2B)＝eq \f(ac,sin Asin C)＝eq \f(\f(3\r(2),4),\f(\r(2),3))＝eq \f(9,4)，
即b2＝eq \f(9,4)×eq \f(1,9)＝eq \f(1,4)，得b＝eq \f(1,2).
感悟提升 三角形面积公式的应用原则
(1)对于面积公式S＝eq \f(1,2)absin C＝eq \f(1,2)acsin B＝eq \f(1,2)bcsin A，一般是已知哪一个角就使用哪一个公式.
(2)与面积有关的问题，一般要用到正弦定理或余弦定理进行边和角的转化.
考向四 多边形中的解三角形问题
例4 (2023·烟台一模)如图，四边形ABCD中，AB2＋BC2＋AB·BC＝AC2.
(1)若AB＝3BC＝3，求△ABC的面积；
(2)若CD＝eq \r(3)BC，∠CAD＝30°，∠BCD＝120°，求∠ACB的值.
解 (1)在△ABC中，cs B＝eq \f(AB2＋BC2－AC2,2AB·BC)＝eq \f(－AB·BC,2AB·BC)＝－eq \f(1,2)，
因为0°＜B＜180°，所以B＝120°.
S△ABC＝eq \f(1,2)AB·BCsin 120°＝eq \f(1,2)×3×1×eq \f(\r(3),2)＝eq \f(3\r(3),4).
(2)由(1)知B＝120°，设∠ACB＝θ，
则∠ACD＝120°－θ，∠ADC＝30°＋θ，∠BAC＝60°－θ.
在△ACD中，由eq \f(AC,sin（30°＋θ）)＝eq \f(CD,sin 30°)，
得AC＝eq \f(sin（30°＋θ）,sin 30°)CD.
在△ABC中，由eq \f(AC,sin 120°)＝eq \f(BC,sin（60°－θ）)，
得AC＝eq \f(sin 120°,sin（60°－θ）)BC.
联立上式，并由CD＝eq \r(3)BC得sin(30°＋θ)sin(60°－θ)＝eq \f(1,4)，
所以sin(60°＋2θ)＝eq \f(1,2)，
由题可知0°＜θ＜60°，
所以60°＜60°＋2θ＜180°，
所以60°＋2θ＝150°，解得θ＝45°，
即∠ACB的值为45°.
感悟提升 平面几何中解三角形问题的求解思路
(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；
(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果.
考向五 三角形中的最值、范围问题
例5(2022·新高考Ⅰ卷)记△ABC的内角A，B，C的对边分别为a，b，c，已知eq \f(cs A,1＋sin A)＝eq \f(sin 2B,1＋cs 2B).
(1)若C＝eq \f(2π,3)，求B；
(2)求eq \f(a2＋b2,c2)的最小值.
[思路分析] (1)化简条件式，利用C＝eq \f(2π,3)消去角A得到角B的三角方程，即可求解.
(2)利用条件式得到A，B的关系式，利用正弦定理把eq \f(a2＋b2,c2)转化为B的三角函数式，利用基本不等式求其最小值.
[规范解答] 解 (1)因为eq \f(cs A,1＋sin A)＝eq \f(sin 2B,1＋cs 2B)，
→eq \a\vs4\al(化倍角为单角以利于计算)
所以eq \f(cs A,1＋sin A)＝eq \f(sin B,cs B)，(2分)
所以cs Acs B＝sin B＋sin Asin B，
eq \x(所以cs（A＋B）＝sin B②)，(4分)
→由cs(A＋B)＝－cs C，角C＝eq \f(2π,3)，进而求B
所以sin B＝－cs C＝－cs eq \f(2π,3)＝eq \f(1,2).
→eq \a\vs4\al(利用B的范围求B)
(2)eq \x(由（1）得cs（A＋B）＝sin B，)
→eq \a\vs4\al(利用（1）题的结论)
所以sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－（A＋B）))＝sin B，
且0→eq \a\vs4\al(根据B与\f(π,2)－（A＋B）的范围确定其关系)
所以eq \f(π,2)－(A＋B)＝B，解得A＝eq \f(π,2)－2B，(8分)
→eq \a\vs4\al(利用正弦定理实现边角互化)
→eq \a\vs4\al(消去角A以利求解)
＝eq \f(cs22B＋sin2B,cs2B)＝eq \f(（2cs2B－1）2＋1－cs2B,cs2B)
→eq \a\vs4\al(化为基本不等式的形式)
≥2eq \r(4cs2B·\f(2,cs2B))－5＝4eq \r(2)－5③，
→eq \a\vs4\al(验证取等号的条件)
所以eq \f(a2＋b2,c2)的最小值为4eq \r(2)－5.(12分)
[满分规则]
❶得步骤分：
①处的实质都是解三角方程，都要注意写清楚角的范围，否则易失步骤分.
❷得关键分：
②处消去角A是本题得解的关键所在.
❸得计算分：
③处利用基本不等式求最小的关键是把目标函数化为其适用形式.
感悟提升 对于解三角形中的证明问题，要仔细观察条件与结论之间的联系，发现二者的差异，利用正弦定理、余弦定理及三角恒等变换把条件转换为结论，即为证明过程.
考向六 三角函数模型
例6 (多选)(2023·福州模拟)如图所示，一半径为4米的水轮，水轮圆心O距离水面2米，已知水轮每60秒逆时针转动一圈，如果当水轮上点P从水中浮现时(图中点P0)开始计时，则( )
A.点P第一次到达最高点需要20秒
B.当水轮转动155秒时，点P距离水面2米
C.当水轮转动50秒时，点P在水面下方，距离水面2米
D.点P距离水面的高度h(米)与t(秒)的函数解析式为h＝4cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t＋\f(π,3)))＋2
答案 ABC
解析 设点P距离水面的高度h(米)和时间t(秒)的函数解析式为
h＝Asin(ωt＋φ)＋Beq \b\lc\(\rc\)(\a\vs4\al\c1(A＞0，ω＞0，|φ|＜\f(π,2)))，
由题意得eq \b\lc\{(\a\vs4\al\c1(hmax＝A＋B＝6，,hmin＝－A＋B＝－2，,T＝\f(2π,ω)＝60，,h（0）＝Asin（ω·0＋φ）＋B＝0，))
解得eq \b\lc\{(\a\vs4\al\c1(A＝4，,B＝2，,ω＝\f(2π,T)＝\f(π,30)，,φ＝－\f(π,6)，))
故h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2，故D错误；
对于A, 令h＝6，即h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2＝6，
解得t＝20，故A正确；
对于B，令t＝155，代入h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2，
解得h＝2，故B正确；
对于C，令t＝50，代入h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2，
解得h＝－2，故C正确.
感悟提升 1.研究y＝Asin(ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题.
2.方程根的个数可转化为两个函数图象的交点个数.
3.三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，利用三角函数的有关知识解决问题.
基础题型训练
一、单选题
1．在中，已知，则（ ）
A．3B．2C．D．
【答案】B
【分析】直接由正弦定理即可得到答案
【详解】由正弦定理，得．
故选：B
2．有一拦水坝的横断面是等腰梯形,它的上底长为6m,下底长为10m,高为,那么此拦水坝斜坡的坡度和坡角分别为
A．B．C．D．
【答案】B
【解析】先求出，则，再解直角三角形得解.
【详解】如图所示,横断面是等腰梯形,,,高，
则,∴,∴.
故选：B
【点睛】本题主要考查解直角三角形的实际应用，意在考查学生对这些知识的理解掌握水平.
3．的内角A，B，C的对边分别为a，b，c．已知，，，则的面积为（ ）
A．B．C．D．
【答案】D
【分析】由余弦定理得出，再求的面积.
【详解】由，得．因为，，，所以，故的面积．
故选：D
4．要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD＝120°，CD＝40 m，则电视塔的高度为（ ）
A．B．
C．D．
【答案】A
【分析】用表达，在△中用余弦定理即可求得结果.
【详解】设，在△中，因为，故可得；
在△中，因为，故可得；
在△中，由余弦定理，
即，整理得：，解得.
即电视塔的高度为.
故选：.
5．在中，，，，则满足条件的有（ ）
A．0个B．1个C．2个D．不确定
【答案】C
【分析】根据题意判断的大小关系，即可得出答案.
【详解】解：因为，，，，
所以，
所以三角形有两个解，即满足条件的有2个.
故选：C.
6．在锐角三角形中，，，分别是角，，的对边，已知，是方程的两个根，且，则c＝（ ）
A．4B．C．D．
【答案】B
【分析】首先根据韦达定理求出，，再根据余弦定理求.
【详解】，是方程的两个根，
，，
因为，
, 是锐角三角形，

根据余弦定理可知
即，

故选：B
【点睛】本题考查解三角形和二次方程韦达定理的综合应用，重点考查计算能力，转化与变形，属于基础题型.
二、多选题
7．某人在处向正东方向走后到达处，他沿南偏西方向走到达处，这时他离出发点，那么的值可以是（ ）
A．B．C．D．
【答案】AB
【分析】根据余弦定理，即可求解.
【详解】如图，由条件可知，，，，，根据余弦定理可知，即，
解得：或
故选：AB
8．的内角的对边分别为，下列结论一定成立的有（ ）
A．
B．若，则
C．若，则是等腰三角形
D．若，则是等腰三角形
【答案】BC
【分析】根据正弦定理，两角和的正弦公式，诱导公式等知识，逐一分析选项，即可得答案.
【详解】对于A：因为中，
所以，故A错误；
对于B：因为，所以，由正弦定理得，
所以，即，故B正确；
对于C：因为，由正弦定理边化角得，
所以，
因为，所以或（舍），所以是等腰三角形，故C正确；
对于D：因为，且，
所以或，即或，
所以是等腰三角形或直角三角形，故D错误.
故选：BC
三、填空题
9．在中，，，，则__________．
【答案】/
【分析】利用正弦定理解三角形即可.
【详解】由正弦定理得，所以，又，所以.
故答案为：.
10．的内角、、所对边分别为、、，已知，则的最大值为__．
【答案】
【解析】由正弦定理，两角和的正弦函数公式，三角形内角和定理，诱导公式化简已知等式，结合，可得，则由正弦定理可求，利用正弦函数的性质即可求其最大值．
【详解】，
由正弦定理可得：，
，，即，
由正弦定理可得，可得，
当为直角时，的最大值为1．
故答案为：1．
11．甲船在岛的正南处， ，甲船以每小时的速度向正北方向航行，同时乙船自出发以每小时的速度向北偏东的方向驶去，甲、乙两船相距最近的距离是_____.
【答案】
【分析】根据条件画出示意图，在三角形中利用余弦定理求解相距的距离，利用二次函数对称轴及可求解出最值.
【详解】假设经过小时两船相距最近，甲、乙分别行至，，
如图所示，可知，，，
．
当小时时甲、乙两船相距最近，最近距离为．
【点睛】本题考查解三角形的实际应用，难度较易.关键是通过题意将示意图画出来，然后将待求量用未知数表示，最后利用函数思想求最值.
12．在中，AB=1，BC=2，以C为直角顶点向外作等腰直角三角形ACD，当∠ABC变化时，线段BD的最大值为______．
【答案】/
【分析】设角，，在三角形中由正弦定理，余弦定理分别表示出的长，角，之间的关系，在中由余弦定理表示出的长，即可求得答案．
【详解】设角，，
在三角形中，，
，
由正弦定理得，，
，
在三角形中，，，，
由余弦定理得，
，
当 即时， 取到最大值 ，
的最大值为：，
故答案为：．
四、解答题
13．在中，，，为边上一点，且．
（1）求；
（2）若，求．
【答案】（1）；（2）．
【分析】（1）在△中，由余弦定理，即可求.
（2）在中，由正弦定理，即可求.
【详解】（1）在△中，，，，
由余弦定理得：，
∴．
（2）在中，，，，
由正弦定理得：，即，
∴．
14．在中，角所对的边分别为，且满足．
(1)求角的值；
(2)若，且，求的取值范围．
【答案】(1);
(2)．
【分析】（1）利用诱导公式，正弦的二倍角公式化简得到，从而求出；
（2）借助正弦定理化边为角的正弦，得到，结合，求出答案.
（1）
由诱导公式可知
所以，
故
化简得：，
因为，所以
故，．
（2）
由正弦定理，
所以，，
故．
因为，所以，
∴，，
∴．
15．中，角A，B，C所对的边分别为a，b，c，，，．
(1)，时，求CD的长度；
(2)若CD为角C的平分线，且，求的面积．
【答案】(1)
(2)
【分析】（1）根据题意，可得，然后根据向量的模长计算公式，即可得到结果；
（2）根据题意，可得，然后结合三角形的面积公式即可得到，从而得到的面积.
【详解】（1）当时，
则
所以，
∴．
（2）因为，
即，∴，又，
∴，则，
∴．
16．已知的角，，的对边分别为，，，且．
(1)求的值；
(2)若，，求．
【答案】(1)
(2)
【分析】（1）利用二倍角公式得到，再由正弦定理将边化角，最后结合诱导公式及两角和的正弦公式计算可得；
（2）由（1）求出，再由余弦定理计算可得.
【详解】（1）解：∵，
∴，
即，
由正弦定理可得，
∵，则，所以，
∴，
∴．
∵，∴．
（2）解：由（1）可知，
而，∴．
∵，，
∴由余弦定理可得，
整理得，解得或（舍去），
∴．
提升题型训练
一、单选题
1．在△ABC中，，则的值是（ ）
A．B．
C．D．
【答案】A
【分析】根据正弦定理直接求解出结果.
【详解】由正弦定理得,
故选：A.
2．在中，角的对边分别为，若，则的值为（ ）
A．B．C．D．
【答案】B
【分析】由向量数量积运算法则及正弦定理得，求出，，再利用余弦定理求出.
【详解】由题意得：，
因为，所以，
由正弦定理得：，
即，
因为，
所以，
故，即，
则，
由余弦定理及得：，
即，解得：.
故选：B
3．已知的三个内角所对的边分别为，且满足，则（ ）
A．B．C．D．
【答案】C
【解析】直接利用余弦定理计算得到答案.
【详解】，，
.
故选：C.
【点睛】本题考查了余弦定理，属于简单题.
4．在中，角的对边为，若，则当取最大值时，的面积是（ ）
A．B．C．D．
【答案】B
【分析】由余弦定理可得：，再利用基本不等式的性质可得的最大值，再利用三角形面积计算公式即可得出．
【详解】解：在中，由余弦定理可得：，当且仅当时取等号．
，
当取最大值时，的面积．
故选：B．
5．如图，四边形中，，，且、的周长相等，则（ ）
A．B．C．D．
【答案】C
【分析】求出，设，可得出，根据已知条件求出的值，可求出的正弦值和余弦值，进一步可求得的正弦值和余弦值，然后利用二倍角的正弦公式可求得结果.
【详解】，，所以，为等腰直角三角形，
所以，，，
设，则，
因为、的周长相等，则，解得，则，
于是，，
故，
.
因此，．
故选：C.
【点睛】方法点睛：在解三角形的问题中，若已知条件同时含有边和角，但不能直接使用正弦定理或余弦定理得到答案，要选择“边化角”或“角化边”，变换原则如下：
（1）若式子中含有正弦的齐次式，优先考虑正弦定理“角化边”；
（2）若式子中含有、、的齐次式，优先考虑正弦定理“边化角”；
（3）若式子中含有余弦的齐次式，优先考虑余弦定理“角化边”；
（4）代数式变形或者三角恒等变换前置；
（5）含有面积公式的问题，要考虑结合余弦定理求解；
（6）同时出现两个自由角（或三个自由角）时，要用到三角形的内角和定理.
6．如图为2022年北京冬奥会首钢滑雪大跳台示意图，为测量大跳台最高点距地面的距离，小明同学在场馆内的A点测得的仰角为，，，（单位：），（点在同一水平地面上），则大跳台最高高度（ ）
A．B．
C．D．
【答案】C
【分析】在中由正弦定理算出，在中，得到.
【详解】在中, ，，所以，又，由正弦定理可得,
,
,
在中，,
所以，（m）
故选：C.
二、多选题
7．的内角､､的对边分别为､､，，，则可以为（ ）
A．7B．8C．9D．10
【答案】AB
【分析】根据正弦定理可得，再根据正弦的范围选择即可
【详解】在中，，，由正弦定理可得，即，所以，因为，所以，所以可以为7，8
故选：AB
8．在中，角A，B，C的对边分别为a，b，c，且，则下列说法正确的有（ ）
A．
B．若，且的面积为，则的最小边长为2
C．若时，是唯一的，则
D．若时，周长的范围为
【答案】ABD
【分析】根据题干已知等式，利用正弦定理、三角和差公式可解得，再根据各个选项的条件逐一求解即可.
【详解】对于选项A：已知等式利用正弦定理化简得：
，整理得： ，即。
，则，故A选项正确；
对于选项B：因为，且的面积为，则由正弦定理得，而又，解得，所以，而，由余弦定理得：,则，所以三角形中边长为最小边，，故B选项正确；
对于选项C：当时，而又，由正弦定理，即，唯一，
，故C选项错误;
对于选项D：
，





，
则有 即，而，
所以周长 的范围为，故D选项正确.
故选：ABD.
三、填空题
9．在中，已知，，，则边上的中线长为________．
【答案】
【分析】先利用余弦定理求得的值,再设中线,利用余弦定理求出中线的值.
【详解】由条件知：,
设中线长为,由余弦定理知：
所以.所以边上的中线长为.
故答案为:.
【点睛】本题主要考查余弦定理的应用,属于基础题.
10．在铺砌领域，有一座数学家们在半个多世纪里一直追寻的“圣杯”，这座圣杯名为“爱因斯坦”，指的是一个可以填满无限平面，且不会自我重复的“非周期性”铺砌块．2023年3月20日，一个由数学家和计算机科学家组成的研究团队，在论文预印网站arXiv上提交了一篇论文，表示他们找到了这样一种由多个相同的“风筝”粘在一起而形成的十三边形（如右图所示），只用此十三边形就能做到单铺砌块，也就是数学家们寻找的“圣杯”．若已知此十三边形最短的边长为1，则此十三边形的面积为_____________．
【答案】
【分析】根据题意，由条件可得，然后由十三边形的面积为即可得到结果．
【详解】
由图可知：，
，∴，∴，，
∴十三边形的面积为．
故答案为:
11．在中，内角，，的对边分别为，，若，且为的外心，为的重心，则的最小值为________．
【答案】
【分析】根据，，利用正弦定理结合两角和与差的三角函数得到，进而求得和外接圆半径，然后建立坐标系，写出外接圆方程，分别表示A，B，C的坐标，进而得到O，G的坐标求解.
【详解】因为，，
由正弦定理得：，
所以，
因为，
所以，即，
因为，
所以
所以外接圆的半径为：
建立如图所示直角坐标系：
则，设，
由，解得，
所以，
所以外接圆的方程为，
所以点C的轨迹是以为圆心，以为半径的圆，
设，
因为G为重心，则， ，
所以，
故答案为：
【点睛】关键点点睛：本题关键是将中的5换为边c，利用正弦定理求得角C，进而求得外接圆方程，再利用坐标法而得解.
12．在锐角三角形中，内角所对的边满足，若存在最大值，则实数的取值范围是__________．
【答案】
【分析】先利用余弦定理结合可得，再利用正弦定理化边为角，再结合三角形内角和定理，求出的关系，从而可将都用表示，再根据三角形为锐角三角形求出的范围，再根据二倍角的余弦公式结合二次函数的性质即可得解.
【详解】由余弦定理可得，则，
由正弦定理可得
，
因为为锐角三角形，则，所以，
又因为函数在内单调递增，所以，可得，
由于为锐角三角形，则，即，解得，
则
，
因为，所以，则，
因为存在最大值，则，解得．
故答案为：．
【点睛】关键点点睛：解决本题的关键是利用余弦定理和正弦定理结合已知条件求得.
四、解答题
13．在中，已知哪些条件可以应用余弦定理解三角形？
【答案】两边及一角、三边
【分析】根据余弦定理的结构特点，即可作出判断.
【详解】当已知两边及一角或已知三边时，可利用余弦定理解三角形.
14．在中，内角所对的边分别为，.
（1）求；
（2）求.
【答案】（1）；（2）.
【分析】（1）由正弦定理即可得到答案；
（2）由三角形面积公式即可求得答案.
【详解】（1）由正弦定理，.
（2）由题意，
.
15．在△中，角A，B，C的对边分别为a，b，c，且，是方程的两个实根.
(1)求和；
(2)若，求的值.
【答案】(1)，，
(2)
【分析】（1）利用韦达定理及其同角三角函数平方关系即可求解；
（2）先利用余弦的二倍角公式恒等变形，再利用正弦定理角化边，最后结合余弦定理即可求解.
【详解】（1）由题意可知，，即，
由韦达定理得， ，
将代入解得，
又∵是△的内角，
∴，
∴，解得，
（2）由得，
根据正弦定理可得，
由余弦定理可得，即，∴，
又∵ ，∴△是等边三角形，
因此.
16．已知某渔船在渔港的南偏东方向，距离渔港约海里的处出现险情，此时在渔港的正上方恰好有一架海事巡逻飞机接到渔船的求救信号，海事巡逻飞机迅速将情况通知了在处的渔政船并要求其迅速赶往出事地点施救．若海事巡逻飞机测得渔船的俯角为，测得渔政船的俯角为，且渔政船位于渔船的北偏东方向上．
(1)计算渔政船与渔港的距离；
(2)若渔政船以每小时海里的速度直线行驶，能否在小时内赶到出事地点？
(参考数据：，，，，，）
【答案】(1)海里
(2)能在小时内赶到出事地点
【分析】（1）在中，利用正切值可求得；再在中，利用正切值可求得；
（2）在中，利用余弦定理可构造方程求得，由可得结论.
（1）
，，，
；
，，，
即渔政船与渔港的距离为海里.
（2）
由题意知：，
在中，由余弦定理得：，
即，解得：（舍）或；
即，
，能在小时内赶到出事地点.
定理
余弦定理
正弦定理
公式
a2＝b2＋c2－2bccs__A；
b2＝c2＋a2－2cacs__B；
c2＝a2＋b2－2abcs__C
eq \f(a,sin A)＝eq \f(b,sin B)＝eq \f(c,sin C)＝2R
常见变形
cs A＝eq \f(b2＋c2－a2,2bc)；
cs B＝eq \f(c2＋a2－b2,2ac)
cs C＝eq \f(a2＋b2－c2,2ab)
(1)a＝2Rsin A，b＝2Rsin__B，c＝2Rsin__C；
(2)sin A＝eq \f(a,2R)，sin B＝eq \f(b,2R)，sin C＝eq \f(c,2R)；
(3)a∶b∶c＝sin__A∶sin__B∶sin__C；
(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin A
A为锐角
A为钝角或直角
图形
关系式
a＝bsin A
bsin Aa≥b
a>b
a≤b
解的个数
一解
两解
一解
一解
无解
所以eq \f(cs A,1＋sin A)＝eq \f(2sin Bcs B,1＋2cs2B－1)，
因为B∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,3)))eq \s\up12(①)，所以B＝eq \f(π,6).(5分)
所以0由正弦定理得eq \f(a2＋b2,c2)＝eq \f(sin2A＋sin2B,sin2C)
＝eq \f(sin2A＋sin2B,1－cs2C)＝eq \f(sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－2B))＋sin2B,1－sin2B)②
＝eq \f(4cs4B－5cs2B＋2,cs2B)＝4cs2B＋eq \f(2,cs2B)－5③(10分)
当且仅当cs2B＝eq \f(\r(2),2)时取等号，