人教A版 (2019)必修 第二册6.4 平面向量的应用课后测评

这是一份人教A版 (2019)必修 第二册6.4 平面向量的应用课后测评，共24页。试卷主要包含了利用正余弦定理解三角形，边角互换及其应用，三角形解的个数，三角形的周长与面积最值等内容，欢迎下载使用。

典例精讲
考点一 利用正余弦定理解三角形
【例1-1】（2022·吉林）在中，若，，，则等于（ ）
A．B．或C．D．或
【例1-2】（2022·上海）在中，若，则________.
【例1-3】（2022·眉山市）在中，角、、所对的边分别是、、，若，，，则等于
【例1-4】（2022·山东菏泽）中，，，则此三角形的外接圆半径是___________.
【一隅三反】
1．（2022·浙江）在中，，则的最小角为 （ ）
A．B．C．D．
2.（2022·北京顺义）在中，，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要件
3．（2022·广东广州·高一期中）（多选）已知中，其内角A，B，C的对边分别为a，b，下列命题正确的有（ ）
A．若，，，则
B．若，，，则
C．若A>B，则
D．若，，则外接圆半径为10
考点二 边角互换及其应用
【例2-1】（2022·广西）在中，角，，所对的边分别为，，，若，则角的值为（ ）
A．B．C．D．
【例2-2】（2022·黑龙江）（多选）在中，，则可以是（ ）
A．B．C．D．
【例2-3】（2022·山西）已知锐角三角形的边长分别为1，3，a，则a的范围是（ ）
A．B．C．D．
【例2-4】（2022·全国·高一课时练习）已知的内角A，B，C所对的边分别为a，b，c，则下列说法中错误的是（ ）
A．若，则一定是等边三角形
B．若，则一定是等腰三角形
C．若，则一定是等腰三角形
D．若，则一定是钝角三角形
【一隅三反】
1．（2022·四川内江）的内角A、B、C所对的边分别为a、b、c，若，，，则（ ）
A．B．C．D．
2．（2022·全国·高一课时练习）已知为的内角所对的边，若，且，则外接圆的半径为（ ）
A．1B．C．2D．4
3．（2022·广西）已知分别为三个内角的对边，且，则是（ ）
A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰或直角三角形
4．（2022·广东广州）已知是钝角三角形，内角A，B，C所对的边分别为，，，，，则最大边的取值范围是_________．（结果用区间表示）
考点三 三角形的面积
【例3-1】（2022·全国·高一课时练习）在中，若，，三角形的面积，则三角形外接圆的半径为（ ）
A．B．2C．D．3
【例3-2】（2022·湖南）在中，内角的对边分别为若的面积为，且，，则外接圆的面积为（ ）
A．B．C．D．
【一隅三反】
1．（2022湖南）在中，内角对应的边分别为，已知，，且，则的面积为 。
2．（2022河北）在中，角，，的对边分别为，，，若，，且，则的面积为______.
3．（2022·上海）在中，、、所对边分别为、、，若，的面积为6，则______．
考点四 三角形解的个数
【例4-1】（2022·全国·高一课时练习）在中，内角A，B，C所对的边分别为a，b，c，则下列条件能确定三角形有两解的是（ ）
A．B．
C．D．
【例4-2】（2022·重庆八中高一期末）在△ABC中，内角A，B，C的对边分别为a，b，c．若，c＝3．且该三角形有两解，则a的值可以为（ ）
A．2B．4C．6D．8
【一隅三反】
1．（2022·全国·高一课时练习）在中，若，，，则此三角形解的情况为（ ）
A．无解B．两解
C．一解D．解的个数不能确定
2．（2022·广西）（多选）在三角形中，，若三角形有两解，则的可能取值为（ ）
A．B．1.1C．D．1.01
3．（2022·浙江）（多选）在中，内角所对的边分别为，下列各组条件中使得有两个解的是（ ）
A．，，B．，，
C．，，D．，，
考点五 三角形的周长与面积最值
【例5-1】（2022·浙江）在中，D的边的中点，．
(1)求角C；
(2)求面积的取值范围．
【例5-2】（2022·广东肇庆）已知在中，角A，B，C的对边分别为a，b，c，.
(1)求角A的大小；
(2)若，求周长的最大值.
【一隅三反】
1．（2022·山东）（多选）已知的斜边长为2．则下列关于的说法中，错误的是（ ）
A．周长的最大值为B．周长的最小值为
C．面积的最大值为2D．面积的最小值为1
2（2022·浙江）在中，D的边的中点，．
(1)求角C；
(2)求面积的取值范围．
3．（2022·四川）在①；②；③这三个条件中任选一个，补充在下面的问题中，并解答问题.问题：在△中，角的对边分别为，且___________
(1)求角B的大小；
(2)，求△周长的取值范围.
6.4.1 正余弦定理（精讲）
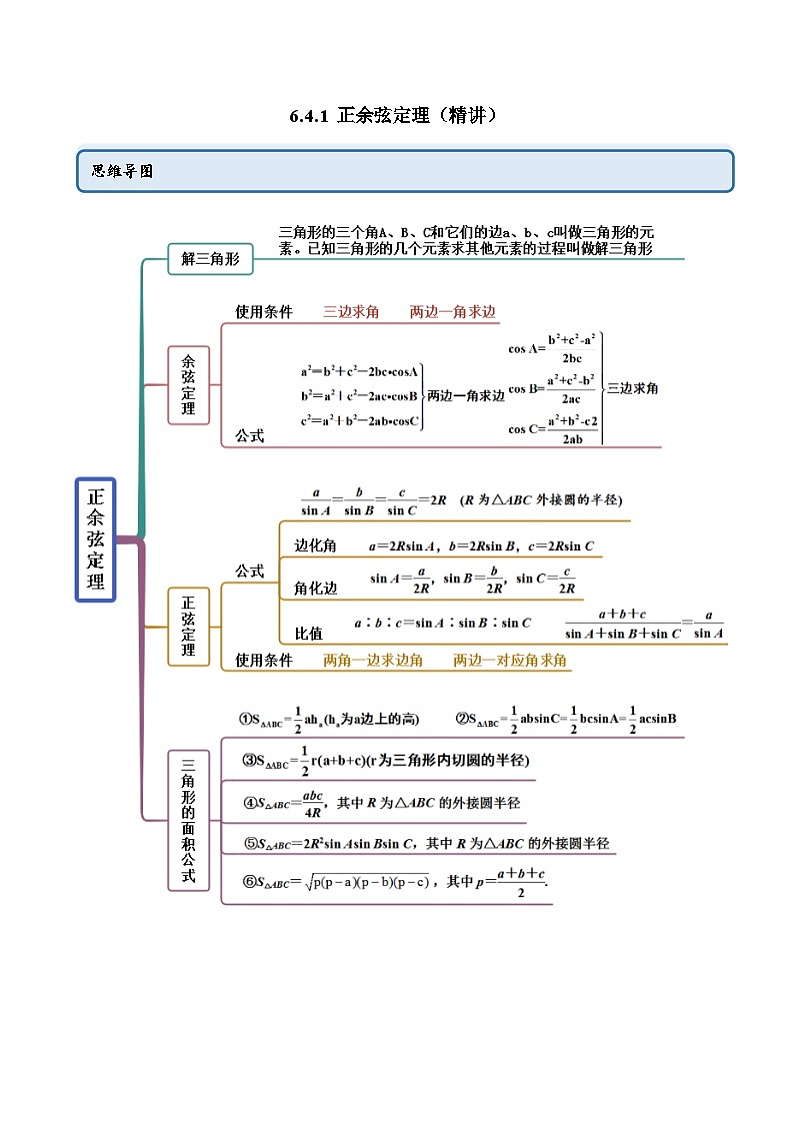
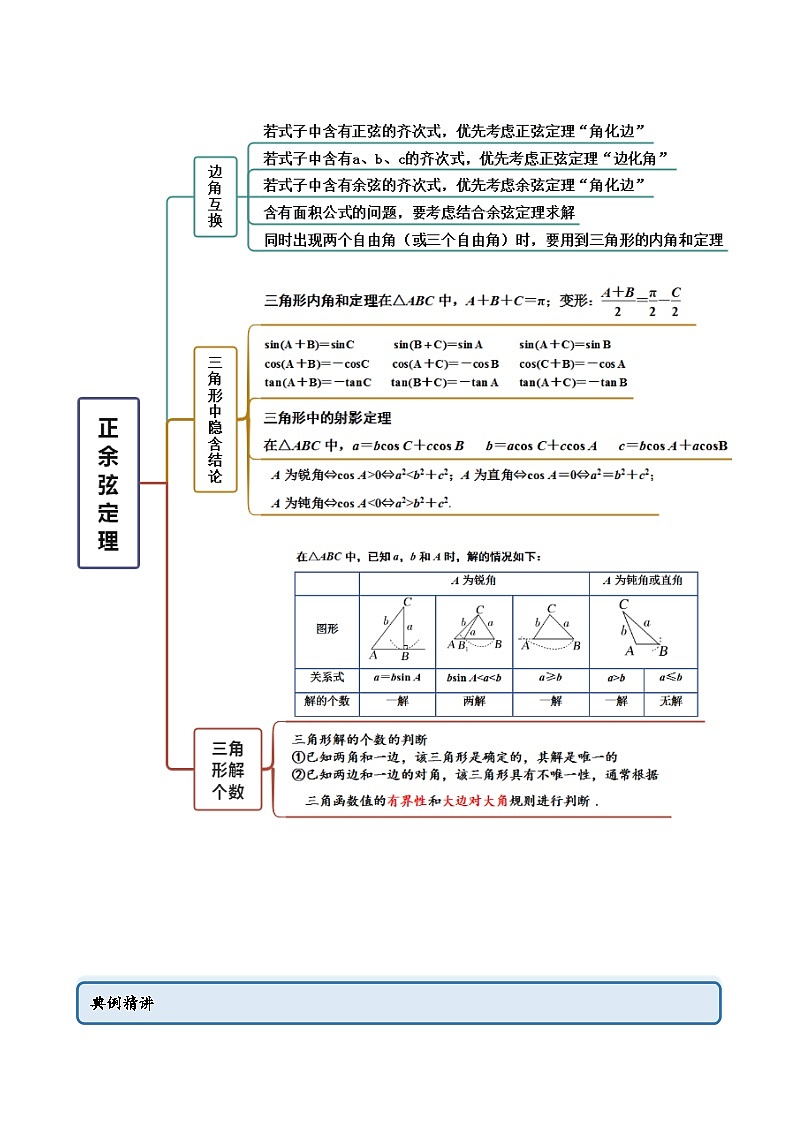
思维导图
典例精讲
考点一 利用正余弦定理解三角形
【例1-1】（2022·吉林）在中，若，，，则等于（ ）
A．B．或C．D．或
【答案】D
【解析】由题意，在中，由正弦定理可得，即，
又由，且，所以或，故选：D.
【例1-2】（2022·上海）在中，若，则________.
【答案】60°
【解析】由余弦定理的推论得，
，.故答案为：60°
【例1-3】（2022·眉山市）在中，角、、所对的边分别是、、，若，，，则等于
【答案】
【解析】，．，
．．
由正弦定理可得：，．
【例1-4】（2022·山东菏泽）中，，，则此三角形的外接圆半径是___________.
【答案】
【解析】由余弦定理得，
因为，所以，设外接圆半径为R，由正弦定理得，解得
故答案为：
【一隅三反】
1．（2022·浙江）在中，，则的最小角为 （ ）
A．B．C．D．
【答案】C
【解析】由已知，在中，，
因为，所以的最小角为，所以，
又因为，所以.故选：C.
2.（2022·北京顺义）在中，，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要件
【答案】B
【解析】中，，由正弦定理，，，
，所以，可为锐角也可为钝角，所以或，
因此“”是“”的必要不充分条件．故选：B．
3．（2022·广东广州·高一期中）（多选）已知中，其内角A，B，C的对边分别为a，b，下列命题正确的有（ ）
A．若，，，则
B．若，，，则
C．若A>B，则
D．若，，则外接圆半径为10
【答案】ABC
【解析】A.因为，，，由余弦定理得：，解得，故A正确；B.因为，，，由正弦定理得：，解得，故B正确；
C.因为，所以，由正弦定理，得(R为外接圆半径)，
所以，故C正确；D.因为，，设R为外接圆半径，
由正弦定理，，所以，故D错误.故选：ABC
考点二 边角互换及其应用
【例2-1】（2022·广西）在中，角，，所对的边分别为，，，若，则角的值为（ ）
A．B．C．D．
【答案】D
【解析】在中，，
由正弦定理可得，
所以，即，
因为，所以，因为，所以.故选：D.
【例2-2】（2022·黑龙江）（多选）在中，，则可以是（ ）
A．B．C．D．
【答案】ABC
【解析】在中，设内角、、的对边分别为、、，
因为，可得，则，
，.故选：ABC.
【例2-3】（2022·山西）已知锐角三角形的边长分别为1，3，a，则a的范围是（ ）
A．B．C．D．
【答案】C
【解析】设角对应的边为，
当是最大边时，，所以，
当不是最大边时，，所以，
所以的取值范围是，故选：C.
【例2-4】（2022·全国·高一课时练习）已知的内角A，B，C所对的边分别为a，b，c，则下列说法中错误的是（ ）
A．若，则一定是等边三角形
B．若，则一定是等腰三角形
C．若，则一定是等腰三角形
D．若，则一定是钝角三角形
【答案】B
【解析】对于A:由正弦定理以及得，因为,所以,故是等边三角形，故A对，
对B:由以及正弦定理得：,
由于，因此,或者,即,或者，故为等腰三角形或者直角三角形，故B错误，
对C:由正弦定理得,
由于在中，,因此可得,
由于,故,故C正确，
对于D:由得，故为钝角，因此D正确故选：B
【一隅三反】
1．（2022·四川内江）的内角A、B、C所对的边分别为a、b、c，若，，，则（ ）
A．B．C．D．
【答案】A
【解析】∵，∴，又，
∴，即，又，∴，又，，
∴.故选：A.
2．（2022·全国·高一课时练习）已知为的内角所对的边，若，且，则外接圆的半径为（ ）
A．1B．C．2D．4
【答案】A
【解析】因为，所以，即，所以．又因为，所以，由正弦定理可得，所以．
故选：A.
3．（2022·广西）已知分别为三个内角的对边，且，则是（ ）
A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰或直角三角形
【答案】D
【解析】由及正弦定理，得,
因为，所以,
所以,即，
当时，因为，所以，
当时，所以，即，
因为所以，所以为等腰或直角三角形.故选：D
4．（2022·广东广州）已知是钝角三角形，内角A，B，C所对的边分别为，，，，，则最大边的取值范围是_________．（结果用区间表示）
【答案】（5，7）
【解析】因为是钝角三角形，最大边为，所以角为钝角，
在中，由余弦定理可得：，可得，
又因为，所以，所以最大边的取值范围是：，故答案为：.
考点三 三角形的面积
【例3-1】（2022·全国·高一课时练习）在中，若，，三角形的面积，则三角形外接圆的半径为（ ）
A．B．2C．D．3
【答案】B
【解析】因为，，三角形的面积，所以,即，解得，
由余弦定理，得，解得，
由正弦定理，得,解得.故选：B.
【例3-2】（2022·湖南）在中，内角的对边分别为若的面积为，且，，则外接圆的面积为（ ）
A．B．C．D．
【答案】B
【解析】由及，得，
所以，即，
于是有，因为，所以，
所以外接圆的半径为，
所以外接圆的面积为．
故选：B.
【一隅三反】
1．（2022湖南）在中，内角对应的边分别为，已知，，且，则的面积为 。
【答案】
【解析】因为，，所以由正弦定理得
即，得因为，所以所以
所以面积
2．（2022河北）在中，角，，的对边分别为，，，若，，且，则的面积为______.
【答案】2
【解析】由余弦定理得，即，解得，
∴，∴，
故.故答案为：2
3．（2022·上海）在中，、、所对边分别为、、，若，的面积为6，则______．
【答案】
【解析】∵，∴可得，
∵的面积为，∴，
∵，∴由余弦定理，可得：
∴解得：故答案为：
考点四 三角形解的个数
【例4-1】（2022·全国·高一课时练习）在中，内角A，B，C所对的边分别为a，b，c，则下列条件能确定三角形有两解的是（ ）
A．B．
C．D．
【答案】B
【解析】如图所示．
若A为锐角，且有两解，则．
对于A选项，，
，但，此时没有两解，A选项不满足条件；
对于B选项，，此时有两解，B选项满足条件；
对于C选项，，且，此时只有一解，C选项不满足条件．
对于D选项，，此时没有两解，D选项不满足条件；
故选：B．
【例4-2】（2022·重庆八中高一期末）在△ABC中，内角A，B，C的对边分别为a，b，c．若，c＝3．且该三角形有两解，则a的值可以为（ ）
A．2B．4C．6D．8
【答案】B
【解析】由正弦定理得，且，所以，即．
【一隅三反】
1．（2022·全国·高一课时练习）在中，若，，，则此三角形解的情况为（ ）
A．无解B．两解
C．一解D．解的个数不能确定
【答案】C
【解析】由正弦定理，得，得，
因为，则，故为锐角，故满足条件的只有一个.故选：C.
2．（2022·广西）（多选）在三角形中，，若三角形有两解，则的可能取值为（ ）
A．B．1.1C．D．1.01
【答案】BD
【解析】若三角形有两解，则满足，故，故选：BD
3．（2022·浙江）（多选）在中，内角所对的边分别为，下列各组条件中使得有两个解的是（ ）
A．，，B．，，
C．，，D．，，
【答案】CD
【解析】A项：因为，所以.
由正弦定理可得，，无解，A错误；
B项：因为，所以.
由正弦定理可得，，只有一个解，B错误；
C项：因为，由正弦定理可得，.
又，所以，此时有两个解，即有两个解，C正确；
D项：因为，由正弦定理可得，.
又，所以，此时有两个解，即有两个解，D正确.故选：CD.
考点五 三角形的周长与面积最值
【例5-1】（2022·浙江）在中，D的边的中点，．
(1)求角C；
(2)求面积的取值范围．
【答案】(1)(2)
【解析】(1)因为，所以
所以，故，又；所以.
(2)在中，由余弦定理可得
因为，，所以，所以，当且仅当时等号成立，
所以，又，当且仅当时等号成立，所以面积．
【例5-2】（2022·广东肇庆）已知在中，角A，B，C的对边分别为a，b，c，.
(1)求角A的大小；
(2)若，求周长的最大值.
【答案】(1)(2)
【解析】(1)由正弦定理，得,即，
由余弦定理得，，又，所以.
(2)由和（1）可知，
则，
得，即，
所以（当且仅当时，取得等号），
所以周长的最大值为.
【一隅三反】
1．（2022·山东）（多选）已知的斜边长为2．则下列关于的说法中，错误的是（ ）
A．周长的最大值为B．周长的最小值为
C．面积的最大值为2D．面积的最小值为1
【答案】BCD
【解析】由题知，设斜边为，则，．
先研究面积：，当且仅当，即时取等号，
所以面积的最大值是1．C、D选项都是错误的；
再研究周长：，，，，，
当且仅当，即时，取等号，所以的最大值为，周长的最大值为，故B选项错误.综上，选BCD．故选：BCD
2（2022·浙江）在中，D的边的中点，．
(1)求角C；
(2)求面积的取值范围．
【答案】(1)(2)
【解析】(1)因为，所以
所以，故，又；所以.
(2)在中，由余弦定理可得
因为，，所以，
所以，当且仅当时等号成立，
所以，又，当且仅当时等号成立，
所以面积．
3．（2022·四川）在①；②；③这三个条件中任选一个，补充在下面的问题中，并解答问题.问题：在△中，角的对边分别为，且___________
(1)求角B的大小；
(2)，求△周长的取值范围.
【答案】(1)；(2).
【解析】(1)
若选①：在△ABC中，因为，
故由可得，
由正弦定理得：，即，
则，又，故.
若选②：，
则，故，
，则，
解得.
若选③：由及正弦定理，，
又，所以，
即，因为，所以，
又，得.
综上所述：选择①②③，都有.
(2)根据（1）中所求，，又，故由余弦定理可得
则，即，当且仅当时取得等号，又，
△周长的取值范围为.