人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直课后测评

这是一份人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直课后测评，共12页。试卷主要包含了定义等内容，欢迎下载使用。
一．直线与平面垂直
（一）定义
垂线段：过一点垂直于已知平面的直线有且只有一条，该点与垂足间的线段叫做这个点到该平面的垂线段，垂线段的长度叫做这个点到该平面的距离.
（二）直线与平面垂直的判定定理
（三）直线与平面垂直的性质定理
二．平面与平面垂直
（一）定义
1.定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.
(2)画法：
(3)记作：α⊥β.
（二）判定定理
（三）性质定理
知识简用
题型一 线线垂直
【例1-1】（2022·高一课时练习）如图，在长方体ABCD－A1B1C1D1的棱中，与棱AB垂直的棱有（ ）
A．2条B．4条
C．6条D．8条
题型二 线面垂直
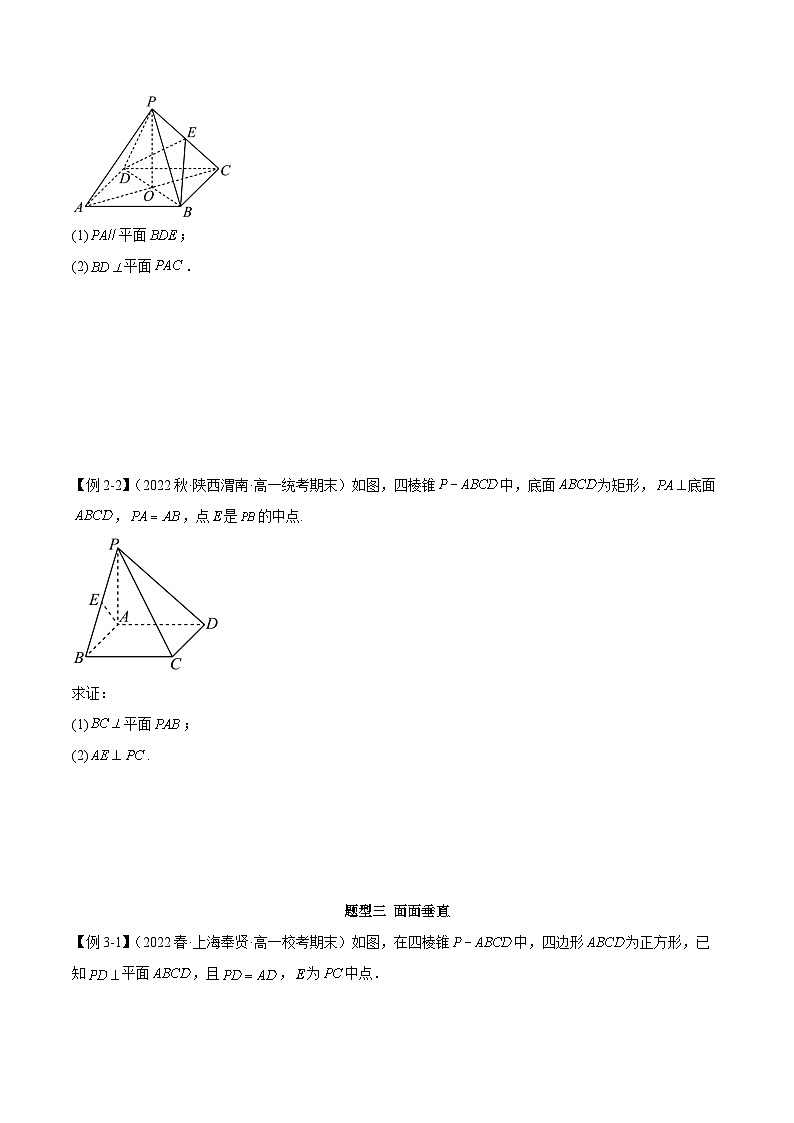
【例2-1】（2022春·广西玉林·高一校考阶段练习）如图，是正方形，是正方形的中心，底面，是的中点． 求证：
(1)平面；
(2)平面．
【例2-2】（2022秋·陕西渭南·高一统考期末）如图，四棱锥中，底面为矩形，底面，，点是的中点.
求证：
(1)平面；
(2).
题型三 面面垂直
【例3-1】（2022春·上海奉贤·高一校考期末）如图，在四棱锥中，四边形为正方形，已知平面，且，为中点．
(1)证明：平面；
(2)证明：平面平面．
【例3-2】（2022秋·陕西渭南·高一校考期末）如图，在直三棱柱ABC﹣A1B1C1中，A1B1＝A1C1，D，E分别是棱BC，CC1上的点（点D不同于点C），且AD⊥DE，F为B1C1的中点．求证：
(1)平面ADE⊥平面BCC1B1；
(2)直线A1F∥平面ADE．
题型四 判断与性质定理的辨析
【例4-1】（2022春·江西上饶·高一校联考阶段练习）已知，是两个不重合的平面，，是两条不重合的直线，下列命题正确的是（ ）
A．若，，则
B．若，，，则
C．若，，则
D．若，，，则
【例4-2】（2022春·河南洛阳·高一统考期末）设，，是三条不同的直线，，，是三个不同的平面，下列说法正确的是（ ）
A．若，，则
B．若，，，，则
C．若，，则
D．若，，，则
定义
如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直
记法
l⊥α
有关概念
直线l叫做平面α的垂线，平面α叫做直线l的垂面，它们唯一的公共点P叫做垂足
图示
画法
画直线与平面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直
文字语言
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直
符号语言
l⊥a，l⊥b，a⊂α，b⊂α，a∩b＝P⇒l⊥α
图形语言
文字语言
垂直于同一个平面的两条直线平行
符号语言
eq \b\lc\ \rc\}(\a\vs4\al\c1(a⊥α,b⊥α))⇒a∥b
图形语言
文字语言
如果一个平面过另一个平面的垂线，那么这两个平面垂直
符号语言
l⊥α，l⊂β⇒α⊥β
图形语言
文字语言
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直
符号语言
α⊥β，α∩β＝l，a⊂α，a⊥l⇒a⊥β
图形语言
8.6.1 空间直线、平面的垂直（学案）
知识自测
一．直线与平面垂直
（一）定义
垂线段：过一点垂直于已知平面的直线有且只有一条，该点与垂足间的线段叫做这个点到该平面的垂线段，垂线段的长度叫做这个点到该平面的距离.
（二）直线与平面垂直的判定定理
（三）直线与平面垂直的性质定理
二．平面与平面垂直
（一）定义
1.定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.
(2)画法：
(3)记作：α⊥β.
（二）判定定理
（三）性质定理
知识简用
题型一 线线垂直
【例1-1】（2022·高一课时练习）如图，在长方体ABCD－A1B1C1D1的棱中，与棱AB垂直的棱有（ ）
A．2条B．4条
C．6条D．8条
【答案】D
【解析】在长方体ABCD－A1B1C1D1的棱中，与棱AB垂直的棱有BC，B1C1，A1D1，AD，AA1，BB1，CC1，DD1，共8条．故选：D.
题型二 线面垂直
【例2-1】（2022春·广西玉林·高一校考阶段练习）如图，是正方形，是正方形的中心，底面，是的中点． 求证：
(1)平面；
(2)平面．
【答案】(1)证明见解析(2)证明见解析
【解析】（1）连接，
四边形为正方形，为中点，又为中点，，
平面，平面，平面.
（2）平面，平面，；
四边形为正方形，，
又，平面，平面.
【例2-2】（2022秋·陕西渭南·高一统考期末）如图，四棱锥中，底面为矩形，底面，，点是的中点.
求证：
(1)平面；
(2).
【答案】(1)证明见解析(2)证明见解析
【解析】（1）∵底面为矩形，∴，
∵底面，底面，∴，
又∵，平面，
∴平面.
（2）∵平面，平面，∴，
∵，是的中点，∴，
又∵，平面，∴平面，
∵平面，∴.
题型三 面面垂直
【例3-1】（2022春·上海奉贤·高一校考期末）如图，在四棱锥中，四边形为正方形，已知平面，且，为中点．
(1)证明：平面；
(2)证明：平面平面．
【答案】(1)证明见解析(2)证明见解析
【解析】（1）连接交于点，连接，
四边形为正方形，为中点，又为中点，，
平面，平面，平面.
（2）平面，平面，；
四边形为正方形，；
，平面，平面，
平面，平面平面.
【例3-2】（2022秋·陕西渭南·高一校考期末）如图，在直三棱柱ABC﹣A1B1C1中，A1B1＝A1C1，D，E分别是棱BC，CC1上的点（点D不同于点C），且AD⊥DE，F为B1C1的中点．求证：
(1)平面ADE⊥平面BCC1B1；
(2)直线A1F∥平面ADE．
【答案】(1)证明见解析；(2)证明见解析.
【解析】（1）∵三棱柱ABC﹣A1B1C1是直三棱柱，∴CC1⊥平面ABC，
∵AD⊂平面ABC，∴AD⊥CC1
又∵AD⊥DE，DE、CC1是平面BCC1B1内的相交直线∴AD⊥平面BCC1B1，
∵AD⊂平面ADE∴平面ADE⊥平面BCC1B1；
（2）∵△A1B1C1中，A1B1＝A1C1，F为B1C1的中点∴A1F⊥B1C1，
∵CC1⊥平面A1B1C1，A1F⊂平面A1B1C1，∴A1F⊥CC1
又∵B1C1、CC1是平面BCC1B1内的相交直线∴A1F⊥平面BCC1B1
又∵AD⊥平面BCC1B1，∴A1F∥AD
∵A1F⊄平面ADE，AD⊂平面ADE，∴直线A1F∥平面ADE．
题型四 判断与性质定理的辨析
【例4-1】（2022春·江西上饶·高一校联考阶段练习）已知，是两个不重合的平面，，是两条不重合的直线，下列命题正确的是（ ）
A．若，，则
B．若，，，则
C．若，，则
D．若，，，则
【答案】D
【解析】对于A，若，，则或或与相交，故A错误．
对于B，若，，，则或或与相交，故B错误．
对于C，若，，则或与相交，故C错误．
对于D，利用线面垂直，及面面垂直的位置关系，可知D正确．
故选：D
【例4-2】（2022春·河南洛阳·高一统考期末）设，，是三条不同的直线，，，是三个不同的平面，下列说法正确的是（ ）
A．若，，则
B．若，，，，则
C．若，，则
D．若，，，则
【答案】D
【解析】利用正方体确定线面之间的位置关系，如图所示，
对于A选项，设AD为m，BC为n，面为，
则满足，，，故A错误；
对于B选项，设AD为m，BC为n，AB为l，面为，
满足，，，，，故B错误；
对于C选项，面为，面为，AD为l,
满足，，，故C错误；
对于D选项，由面面平行性质定理：
两个平行平面，分别和第三个平面相交，交线平行，
所以，，，可得.
故D正确.
故选：D.
定义
如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直
记法
l⊥α
有关概念
直线l叫做平面α的垂线，平面α叫做直线l的垂面，它们唯一的公共点P叫做垂足
图示
画法
画直线与平面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直
文字语言
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直
符号语言
l⊥a，l⊥b，a⊂α，b⊂α，a∩b＝P⇒l⊥α
图形语言
文字语言
垂直于同一个平面的两条直线平行
符号语言
eq \b\lc\ \rc\}(\a\vs4\al\c1(a⊥α,b⊥α))⇒a∥b
图形语言
文字语言
如果一个平面过另一个平面的垂线，那么这两个平面垂直
符号语言
l⊥α，l⊂β⇒α⊥β
图形语言
文字语言
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直
符号语言
α⊥β，α∩β＝l，a⊂α，a⊥l⇒a⊥β
图形语言