

高中数学第八章 立体几何初步8.6 空间直线、平面的垂直同步测试题
展开典例精讲
考点一 线线角
【例1】(2022·高一课前预习)如图,在正方体ABCD-A1B1C1D1中,
(1)AC和DD1所成的角是________;
(2)AC和D1C1所成的角是________;
(3)AC和B1D1所成的角是________;
(4)AC和A1B所成的角是________.
【一隅三反】
1.(2022·高一课前预习)在正方体中,则直线与直线所成角大小为( )
A.B.C.D.
2.(2022春·全国·高一期末)如图,在四面体ABCD中,E,F分别是AC与BD的中点,若CD=2AB=4,EF⊥BA,则EF与CD所成的角为( )
A.90°B.45°C.60°D.30°
3(2022春·四川雅安·高一统考期末)已知正三棱柱中,,,点为的中点,则异面直线与所成角的余弦值为( )
A.B.C.D.
考点二 线面角
【例2】(2022·全国·高一假期作业)如图,在三棱柱中,在底面的射影为的中点,则直线与平面所成角的正弦值为___________.
【一隅三反】
1.(2022春·河北沧州·高一统考期末)如图,在直三棱柱中,,且是棱的中点,是棱上靠近的四等分点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
2.(2022春·贵州六盘水·高一统考期末)如图,在三棱锥中,平面ABC,D是PB上一点,且平面PBC.
(1)求证:;
(2)若,M是PC的中点,求直线BM与平面ABC所成角的大小.
3.(2022·高一单元测试)如图,在直角梯形ABCD中,,AB⊥AD,且,现以AD为一边向形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图2.
(1)求证:平面BEC;
(2)求证:BC⊥平面BDE;
(3)求直线BC与平面ADEF所成角的正弦值.
考点三 二面角
【例3】(2022春·江西宜春·高一江西省万载中学校考阶段练习)如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
(1)求证:平面;
(2)求二面角的大小.
【一隅三反】
1.(2022·高一课时练习)如图,已知正方体.
(1)求二面角的正切值的大小;
(2)求二面角的正切值的大小.
2.(2022春·广东肇庆·高一统考期末)如图,在三棱柱中,侧面为菱形,,且,.
(1)证明:平面ABC⊥平面;
(2)若,求二面角的余弦值.
3.(2022春·山东聊城·高一山东聊城一中校考阶段练习)如图,在直角梯形ABCD中,,,,点E是BC的中点. 将沿BD折起,使,连接AE、AC、DE,得到三棱锥.
(1)求证:平面ABD;
(2)若,求二面角的大小.
考点七 空间距离
【例7】(2022·高一课时练习)如图,已知正方体的棱长为1.
(1)点到平面的距离为______;
(2)直线和平面的距离为______;
(3)直线和平面的距离为______.
【一隅三反】
1.(2021春·山西太原·高一统考期末)如图,在长方体中,..则直线与平面的距离为( )
A.B.C.D.
2.(2022·高一课时练习)在长方体中,有一过且与平面平行的平面,棱,,则平面与平面的距离是_________.
3.(2022·高一课时练习)如图,在长方体中,,,.
(1)求点和点C的距离;
(2)求点到棱BC的距离;
(3)棱和平面ABCD的距离.
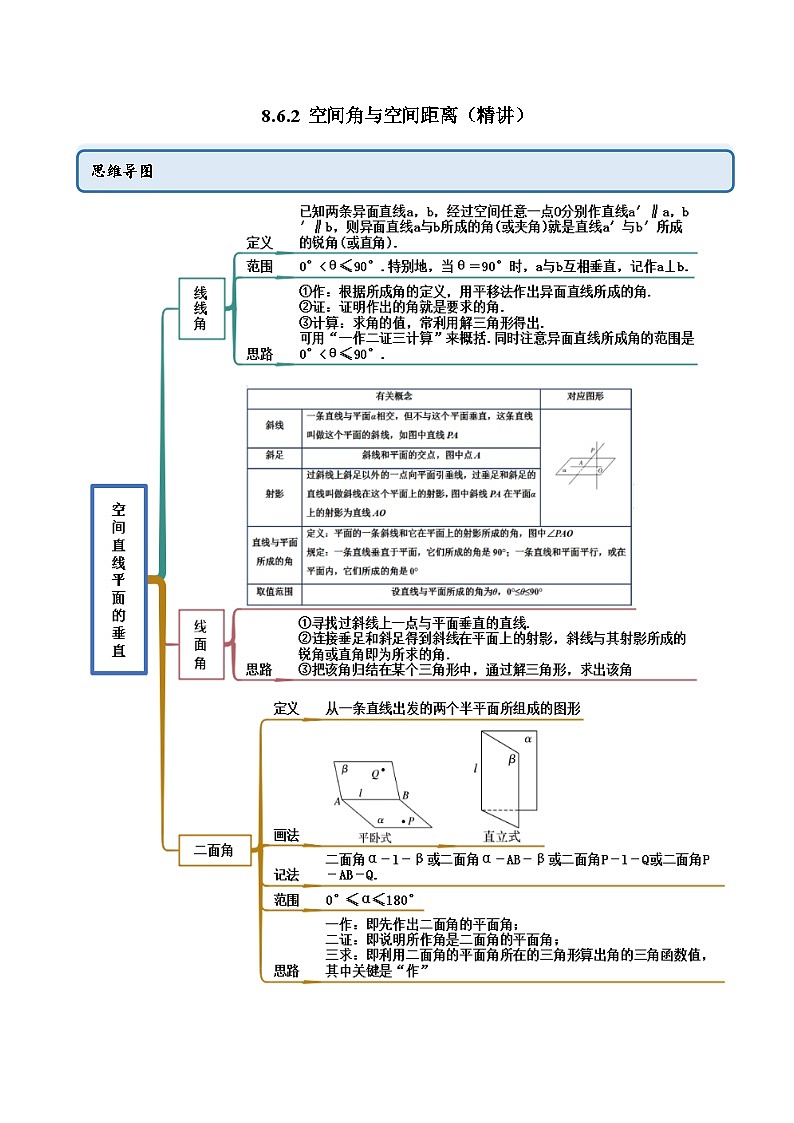
8.6.2 空间角与空间距离(精讲)
思维导图
典例精讲
考点一 线线角
【例1】(2022·高一课前预习)如图,在正方体ABCD-A1B1C1D1中,
(1)AC和DD1所成的角是________;
(2)AC和D1C1所成的角是________;
(3)AC和B1D1所成的角是________;
(4)AC和A1B所成的角是________.
【答案】(1)90°或 (2) 45°或 (3)90°或 (4)60°或
【解析】(1)根据正方体的性质可得平面,所以AC和DD1所成的角是90°.
(2)∵D1C1DC,所以∠ACD即为AC和D1C1所成的角,由正方体的性质得∠ACD=45°.
(3)∵BDB1D1,BD⊥AC,∴B1D1⊥AC,即AC和B1D1所成的角是90°.
(4)∵A1BD1C,△ACD1是等边三角形,所以AC和A1B所成的角是60°.
故答案为:90°或;45°或;90°或;60°或.
【一隅三反】
1.(2022·高一课前预习)在正方体中,则直线与直线所成角大小为( )
A.B.C.D.
【答案】C
【解析】设正方体的棱长为,连接,
因为且,所以四边形是平行四边形,
可得,
所以或其补角即为直线与直线所成角,
在中,,所以,
所以直线与直线所成角大小为,
故选:C.
2.(2022春·全国·高一期末)如图,在四面体ABCD中,E,F分别是AC与BD的中点,若CD=2AB=4,EF⊥BA,则EF与CD所成的角为( )
A.90°B.45°C.60°D.30°
【答案】D
【解析】设G为AD的中点,连接GF,GE
则GF,GE分别为△ABD,△ACD的中线.
∴ ,且,,且,则EF与CD所成角的度数等于EF与GE所成角的度数
又EF⊥ AB,
∴ EF⊥ GF
则△GEF为直角三角形,GF=1,GE=2,∠GFE=90°
∴ 在直角△GEF中,
∴ ∠GEF=30°.
故选:D.
3(2022春·四川雅安·高一统考期末)已知正三棱柱中,,,点为的中点,则异面直线与所成角的余弦值为( )
A.B.C.D.
【答案】A
【解析】如图所示,取的中点,连接,
因为点为的中点,可得,
所以异面直线与所成角即为直线与所成角,设,
在正中,由,可得,
在直角中,可得,
在直角中,可得,
在中,
由余弦定理可得.
故选:A.
考点二 线面角
【例2】(2022·全国·高一假期作业)如图,在三棱柱中,在底面的射影为的中点,则直线与平面所成角的正弦值为___________.
【答案】
【解析】如图所示:
取的中点M,连接,
因为,又,
所以,又,
所以平面,又平面,
所以平面平面,
又平面平面,
作,则平面,
因为,
所以直线与平面所成角的正弦值为.
故答案为:
【一隅三反】
1.(2022春·河北沧州·高一统考期末)如图,在直三棱柱中,,且是棱的中点,是棱上靠近的四等分点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】(1),
,
,可理,
,
,
又平面.
(2)如图,取的中点,连接.
.
由(1)知平面平面,
所以平面平面,又平面平面,
平面,所以是直线在平面内的射影,
即为直线与平面所成的角.
,
在中,
,
所以直线与平面所成角的正弦值为.
2.(2022春·贵州六盘水·高一统考期末)如图,在三棱锥中,平面ABC,D是PB上一点,且平面PBC.
(1)求证:;
(2)若,M是PC的中点,求直线BM与平面ABC所成角的大小.
【答案】(1)证明详见解析(2)
【解析】(1)由于平面ABC,平面,所以.
由于平面PBC,平面,所以,
由于平面,所以平面,
由于平面,所以.
(2)设是的中点,连接,
由于是的中点,所以,所以平面,
所以是直线与平面所成角,
由于,直角三角形中,,
所以,所以.
3.(2022·高一单元测试)如图,在直角梯形ABCD中,,AB⊥AD,且,现以AD为一边向形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图2.
(1)求证:平面BEC;
(2)求证:BC⊥平面BDE;
(3)求直线BC与平面ADEF所成角的正弦值.
【答案】(1)证明见解析;(2)证明见解析;(3).
【解析】(1)取EC中点N,连接MN,BN,如图,在△EDC中,M为ED的中点,
则,且,而,,即有,
因此四边形ABNM为平行四边形,有,因平面BEC,且平面BEC,
所以平面BEC.
(2)由正方形ADEF知,ED⊥AD,而平面ADEF⊥平面ABCD,且平面ADEF平面ABCD=AD,
平面ADEF,则ED⊥平面ABCD,而平面ABCD,即有,
在直角梯形ABCD中,AB⊥AD,,则,,
而,有,即,
因此,又,平面BDE,
所以平面BDE.
(3)延长CB与DA交于P点,由(2)知,而,,面ADEF,
于是得CD⊥面ADEF,即为直线BC与平面ADEF所成角,而,则,所以直线BC与平面ADEF所成角的正弦值.
考点三 二面角
【例3】(2022春·江西宜春·高一江西省万载中学校考阶段练习)如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
(1)求证:平面;
(2)求二面角的大小.
【答案】(1)见解析(2)
【解析】(1)由 平面可得 又 ,所以平面,所以 ;
连交于点 ,连,
则是 的中位线,,而平面,
平面,平面.
(2)取的中点,连,则是的中位线,
,又平面,平面;
因为平面,故,
又,底面为平行四边形,,,
而分别为中点,所以;
而是的中位线,,
而平面,故平面,
而平面,故,
所以是二面角的平面角.
又 ;
,而二面角与二面角互补,
故所求二面角的大小为.
【一隅三反】
1.(2022·高一课时练习)如图,已知正方体.
(1)求二面角的正切值的大小;
(2)求二面角的正切值的大小.
【答案】(1);(2).
【解析】(1)连接,交于,
因为四边形为正方形,所以,
又平面,平面,
所以,平面,,
所以平面,因为平面,,
所以是二面角的平面角,
设,
在中,,,
所以,由,
所以,
所以二面角的正切值为.
(2)连接,其中点为的中点,
因为,,
所以,,
所以为二面角的平面角,
在中,,,
所以
二面角的正切值为.
2.(2022春·广东肇庆·高一统考期末)如图,在三棱柱中,侧面为菱形,,且,.
(1)证明:平面ABC⊥平面;
(2)若,求二面角的余弦值.
【答案】(1)证明见解析;
(2).
【解析】(1)连接,如图,
由是菱形,所以.
又,,
所以平面,故,
又,,
所以AB⊥平面,又平面ABC.
所以平面ABC⊥平面.
(2)过在平面内引直线垂直于AC,O为垂足,过O在平面ABC内引直线OH垂直于BC,H为垂足,连接.
由平面ABC⊥平面,平面平面,
所以平面ABC,所以,.
又OH⊥BC,,
所以BC⊥平面,
故为二面角的平面角.
设,
由,可知O为AC的中点,
所以.又,平面,平面,
所以AB⊥AC,所以.
所以.
所以,
所以二面角的余弦值为.
3.(2022春·山东聊城·高一山东聊城一中校考阶段练习)如图,在直角梯形ABCD中,,,,点E是BC的中点. 将沿BD折起,使,连接AE、AC、DE,得到三棱锥.
(1)求证:平面ABD;
(2)若,求二面角的大小.
【答案】(1)证明见解析
(2).
【解析】(1)由于平面,
所以平面.由于平面,所以.
由于平面,
所以平面.
(2)分别取的中点,连接,
由于分别是的中点,所以,
由于平面,所以平面,
由于平面,所以.
由于分别是的中点,所以,
由于,所以,
由于平面,所以平面,
所以是二面角的平面角.
在中,,
所以,则为锐角,且,
所以二面角的平面角为.
考点七 空间距离
【例7】(2022·高一课时练习)如图,已知正方体的棱长为1.
(1)点到平面的距离为______;
(2)直线和平面的距离为______;
(3)直线和平面的距离为______.
【答案】(1) 1 (2)1 (3)
【解析】(1)在正方体中,平面,所以点到平面的距离为;
(2)在正方体中,连接,如图,
,,则四边形是平行四边形,有,
而平面,平面,则有平面,
于是得直线和平面的距离等于点到平面的距离,
因平面,则点到平面的距离为,
所以直线和平面的距离为1;
(3)在正方体中,连接,,
而平面,平面,则平面,
因此直线和平面的距离等于点到平面的距离,
连,由正方形得,而平面,平面,
因此,因,平面,则平面,而,
所以直线和平面的距离为.故答案为:1;1;
【一隅三反】
1.(2021春·山西太原·高一统考期末)如图,在长方体中,..则直线与平面的距离为( )
A.B.C.D.
【答案】C
【解析】因为为长方体,所以面⊥面ABCD,
过A作AE⊥BD于E,则AE⊥面,所以直线与平面的距离为AE.
在直角三角形ABD中,由等面积法可得:
故选:C
2.(2022·高一课时练习)在长方体中,有一过且与平面平行的平面,棱,,则平面与平面的距离是_________.
【答案】
【解析】因为平面平面,平面,所以到平面的距离即为平面与平面间的距离,易知平面,从而点A到平面的距离即为所求的距离.
如图,过点A作于点.
因为平面,平面
所以平面平面,
又平面平面=
所以平面,则即为所求.
在中,,,则,
因为,所以.
故平面与平面的距离为.
故答案为:
3.(2022·高一课时练习)如图,在长方体中,,,.
(1)求点和点C的距离;
(2)求点到棱BC的距离;
(3)棱和平面ABCD的距离.
【答案】(1);(2)5cm;(3)3cm.
【解析】(1)如图,连接、AC,
∵平面ABCD,而平面ABCD,
∴,
由勾股定理,得;
(2)如图,连接,∵平面,而平面,
∴.
∴就是点 到棱 BC 的距离,
.
∴点到棱 BC 的距离是5cm;
(3)显然棱平面ABCD,平面ABCD,
∴就是棱和平面ABCD的距离,∵,
∴棱和平面ABCD的距离是3cm.
数学必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直测试题: 这是一份数学必修 第二册<a href="/sx/tb_c4000306_t7/?tag_id=28" target="_blank">第八章 立体几何初步8.6 空间直线、平面的垂直测试题</a>,共14页。试卷主要包含了定义,范围,画法,记法,二面角的平面角等内容,欢迎下载使用。
必修 第二册8.6 空间直线、平面的垂直一课一练: 这是一份必修 第二册<a href="/sx/tb_c4000306_t7/?tag_id=28" target="_blank">8.6 空间直线、平面的垂直一课一练</a>,共25页。试卷主要包含了线面垂直,面面垂直,线线垂直,判断与性质定理的辨析等内容,欢迎下载使用。
人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000305_t7/?tag_id=28" target="_blank">第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题</a>,共42页。试卷主要包含了线线平行,等角性质,线面平行,面面平行,判断定理与性质定理辨析,距离相关问题等内容,欢迎下载使用。













