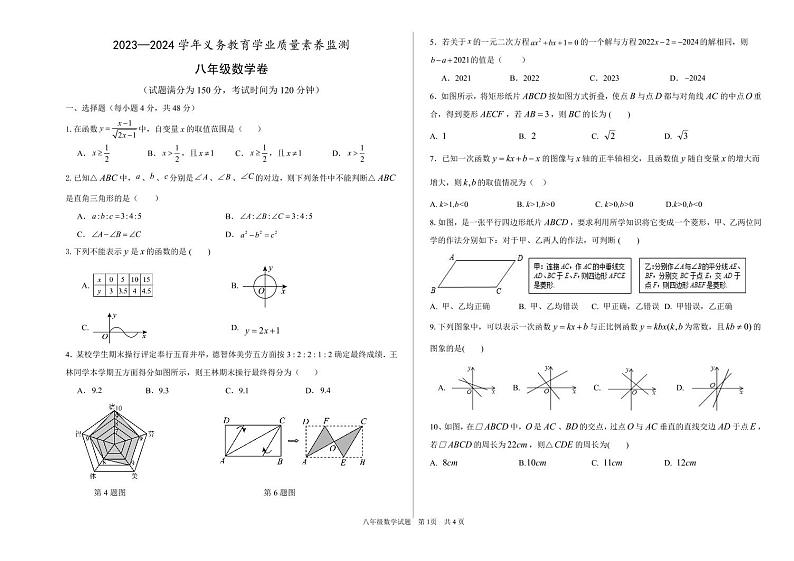
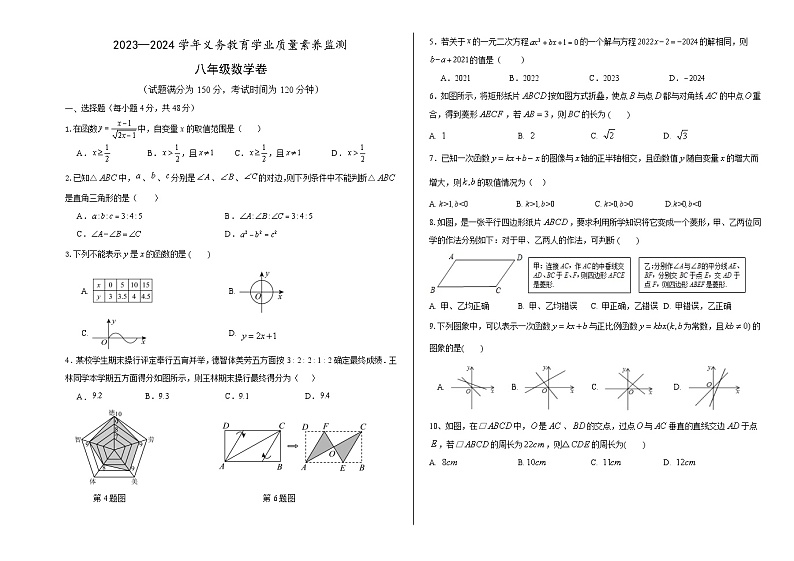
山东省德州市陵城区2023—2024学年八年级下学期期末考试数学试题

这是一份山东省德州市陵城区2023—2024学年八年级下学期期末考试数学试题，文件包含八年级学业水平检测数学试题pdf、教研室提供山东省德州市陵城区2023-2024学年八年级下学期期末考试数学试题docx、八年级答题卡docx、八年级答题卡pdf等4份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。

（试题满分为150分，考试时间为120分钟）
选择题（每小题4分，共48分）
1.在函数中，自变量x的取值范围是（ ）
A． B．，且 C．，且 D．
2.已知△中，、、分别是、、的对边，则下列条件中不能判断△是直角三角形的是（ ）
A．B．
C．D．
3.下列不能表示是的函数的是( )
A. B.
C. D.
4．某校学生期末操行评定奉行五育并举，德智体美劳五方面按3 : 2 : 2 : 1 : 2确定最终成绩．王林同学本学期五方面得分如图所示，则王林期末操行最终得分为（ ）
B．9.3C．9.1D．

第4题图 第6题图
5．若关于的一元二次方程的一个解与方程的解相同，则的值是（ ）
A．2021B．2022C．2023D．
6．如图所示，将矩形纸片按如图方式折叠，使点与点都与对角线的中点重合，得到菱形，若，则的长为( )
A. B. C. D.
7．已知一次函数的图像与轴的正半轴相交，且函数值随自变量的增大而增大，则的取值情况为（ ）
A. k>1,b<0 B. k>1,b>0 C. k>0,b>0 D.k>0,b<0
8.如图，是一张平行四边形纸片，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：对于甲、乙两人的作法，可判断( )
A. 甲、乙均正确B. 甲、乙均错误C. 甲正确，乙错误D. 甲错误，乙正确
9.下列图象中，可以表示一次函数与正比例函数为常数，且的图象的是( )
A. B. C. D.
10、如图，在□中，是、的交点，过点与垂直的直线交边于点，若□的周长为，则△的周长为( )
A. B. C. D.


第10题图 第11题图 第12题图
11.某通信公司就宽带上网推出三种月收费方式．这三种收费方式每月所需的费用与上网时间之间的函数关系如图所示，则下列判断错误的是( )
A. 每月上网时间不足时，选择方式最省钱
B. 每月上网费用为元时，方式可上网的时间比方式多
C. 每月上网时间为时，选择方式最省钱
D. 每月上网时间超过时，选择方式最省钱
如图，正方形的对角线，相交于点，是边上一点，连接，过点作，交于点，连接，若正方形边长为，下列结论：
①;②;③;④△MON始终是等腰直角三角形; ⑤△MDN周长的最小值为 ，面积的最小值为 . 其中正确的为( )
①②④B.①②③④ C.①②④⑤ D. ①②③④⑤
填空题（每小题4分，共24分）
电流通过导线时会产生热量．电流（单位：）、导线电阻R（单位：）、通电时间（单位：）与产生的热量（单位：）满足：．已知导线的电阻，的时间导线产生的热量，则电流为 ．（结果用二次根式表示）
14.如图，在菱形中，，相交于点，且于点，若，则的长等于______．

第14题图 第15题图 第16题图
15.已知关于的一次函数与的图象如图所示，则关于的不等式的解集是___________．
16. 如图，在平面直角坐标系中，，是轴上的两点，是直线上的一个动点，当的值最小时，点的坐标为______________．
17. 已知一次函数,若当时，函数有最小值，则的值为 .
18. 关于函数，给出下列说法正确的是__________．
①当时，该函数是一次函数；
②若点，在该函数图象上，且，则；
③若该函数不经过第四象限，则；
④该函数恒过定点．
三、解答题（7小题，共78分）
19.（本题8分）
（1）计算 （2） 解方程
（本题10分）某校开展了“预防溺水、珍爱生命”的安全知识竞赛．先从该校七、八年级中各随机抽取10 名学生的竞赛成绩（百分制）进行整理、描述和分析（竞赛成绩用x表示，共分成四组，A．，B．，C．，D．）．
部分信息如下：
七年级10名学生竞赛成绩：81，86，99，95，90，99，100，82，89，99；
八年级10名学生竞赛成绩在C组中的数据：94，94，91．
七、八年级抽取的学生竞赛成绩统计表 八年级抽取的学生竞赛成绩扇形统计图

根据以上信息，解答下列问题：
(1)__________，__________，__________，__________；
(2)根据以上数据，你认为该校七、八年级中哪个年级学生安全知识竞赛成绩更好？请说明理由；
(3)若该校七、八年级共2000人参加了此次竞赛活动，其中八年级占60%，估计八年级参加此次竞赛活动获得优秀成绩的学生有多少人．
（本题10分）已知关于的一元二次方程．
（1）若方程有两个实数根，求的取值范围；
（2）若方程的两个根为、且，求的值.
（本题12分）
如图，平行四边形中，，过点作∥交的延长线于点，点为的中点，连接．
（1）求证：四边形是矩形；
（2）若，且，求四边形的周长．
23.（本题12分）某服装店同时购进甲、乙两种款式的运动服共套，进价和售价如表中所示，设购进甲款运动服套（为正整数），该服装店售完全部甲、乙两款运动服获得的总利润为元．
（1）求与的函数关系式．
（2）该服装店计划最多投入万元购进这两款运动服，且最多购进甲运动服240套，则甲、乙两款运动服全部售完后，服装店可获得的最大利润是多少元？
（3）在（2）的条件下，若服装店购进甲款运动服的进价降低元（其中且），其他条件不变，请写出使该服装店获得最大销售利润的购进方案．
24.（本题12分）如果我们身旁没有量角器或三角尺，又需要作60°，30°，15°等大小的角，可以采用下面的方法：
第一：对折矩形纸片，使与重合，得到折痕，把纸片展平．
第二：再一次折叠纸片，使点落在上，并使折痕经过点，得到折痕和线段．
（1）请问图中∠1、∠2和∠3有什么关系？证明你的结论．
（2）在第（1）题图中，延长交于点，延长交于点，连接，判断四边形的形状并证明．
（3）在第（2）题图中，过点作于点，得出一个以为宽的黄金矩形（黄金矩形就是符合黄金比例的矩形，即宽与长的比值为），若已知，求的长．
25.（本题14分）某班“数学兴趣小组”根据学习一次函数的经验，对函数的图象和性质进行了研究．探究过程如下，请补充完整．
(1)自变量的取值范围是全体实数，表格是与的几组对应值：
其中，______；
(2)如图1，在平面直角坐标系中，描出了以上表格中部分对应值为坐标的点，并画出了函数图象的一部分，请画出该函数图象的另一部分；

图1
(3)①观察函数图象发现，该函数图象的最低点M坐标是______；
②当时，随的增大而减小；当时，随的增大而______；
③若关于的方程只有一个解，则的取值范围是______．
(4)若点是函数的图像上的一动点，过点作轴于点，设点的横坐标为，△的面积为.请写出与之间的关系式，并求出时点的坐标.
运动服款式
甲款
乙款
进价/（元/套）
售价/（元/套）
150
…
-3
-2
-1
0
1
2
3
4
5
…
…
5
4
2
1
0
1
2
3
…