2025年高考数学精品教案第六章 平面向量 复数 第3讲 平面向量的数量积及应用

这是一份2025年高考数学精品教案第六章 平面向量 复数 第3讲 平面向量的数量积及应用，共19页。
学生用书P117
1.向量的夹角
注意 确定向量的夹角时应注意“共起点”.
思维拓展
1.两个向量夹角的范围为[0，π]，两条直线夹角的范围为[0，π2].
2.（1）两个向量a，b的夹角为锐角⇔a·b＞0且向量a，b不共线；
（2）两个向量a，b的夹角为钝角⇔a·b＜0且向量a，b不共线.
2.平面向量的数量积
已知两个非零向量a与b的夹角为θ，我们把数量⑤ ｜a｜｜b｜csθ 叫做向量a与b的数量积，记作⑥ a·b .
注意 零向量与任一向量的数量积为0.
3.投影与投影向量
如图，过AB的起点A和终点B，分别作向量CD所在直线的垂线，垂足分别为A1，B1，得到A1B1，我们称上述变换为向量a向向量b⑦ 投影 ，A1B1叫做向量a在向量b上的⑧ 投影向量 .
设与b方向相同的单位向量为e，a与b的夹角为θ，则A1B1＝｜a｜cs θe.
4.向量数量积的运算律
对于向量a，b，c和实数λ，有
（1）a·b＝b·a；
（2）（λa）·b＝λ（a·b）＝a·（λb）；
（3）（a＋b）·c＝a·c＋b·c.
注意 （1）向量数量积的运算不满足乘法结合律，即（a·b）·c不一定等于a·（b·c），这是由于（a·b）·c表示一个与c共线的向量，a·（b·c）表示一个与a共线的向量，而c与a不一定共线.
（2）a·b＝a·c（a≠0）b＝c，等式两边不能约去同一个向量.
（3）平方差公式、完全平方公式仍适用.
5.平面向量数量积的有关结论
已知非零向量a＝（x1，y1），b＝（x2，y2），a与b的夹角为θ.
1.以下说法正确的是（ A ）
A.两个向量的数量积是一个实数，向量的加法、减法、数乘运算的运算结果是向量
B.由a·b＝0可得a＝0或b＝0
C.（a·b）·c＝a·（b·c）
D.已知两个非零向量a与b的夹角为θ，若a·b＞0，则θ为锐角
2.[教材改编]已知向量a＝（1＋x，x－3），b＝（1－x，2），a·b＝－4，则a＋2b与b的夹角为（ B ）
A.π3B.π4C.2π3D.3π4
解析 因为a·b＝－4，所以（1＋x）（1－x）＋2（x－3）＝－4，得x＝1.所以a＝（2，－2），b＝（0，2），所以a＋2b＝（2，2），｜a＋2b｜＝22＋22＝22，｜b｜＝2，所以cs＜a＋2b，b＞＝（a+2b）·b｜a+2b||b｜＝422×2＝22.又＜a＋2b，b＞∈[0，π]，所以a＋2b与b的夹角为π4.故选B.
3.[2022全国卷甲]已知向量a＝（m，3），b＝（1，m＋1）.若a⊥b，则m＝ －34 .
解析 ∵a⊥b，∴a·b＝m＋3（m＋1）＝4m＋3＝0，解得m＝－34.
4.已知点A（－1，1），B（1，2），C（－2，－1），D（3，4），则AB在CD方向上的投影向量为 （32，32） .
解析 依题意，得CD＝（5，5），则与CD同向的单位向量e＝CD｜CD｜＝（22，22），AB＝（2，1），则AB在CD方向上的投影向量为AB·CD｜CD｜·e＝10+552（22，22）＝322（22，22）＝（32，32）.
5.[易错题]已知平面内三个向量a，b，c两两夹角相等，且｜a｜＝｜b｜＝1，｜c｜＝3，则｜a＋b＋c｜＝ 2或5 .
解析 当a，b，c共线时，｜a＋b＋c｜＝｜a｜＋｜b｜＋｜c｜＝5；当a，b，c两两夹角为2π3时，a·b＝－12，a·c＝b·c＝－32.｜a＋b＋c｜＝｜a｜2＋｜b｜2＋｜c｜2+2a·b+2a·c+2b·c＝1+1+9－1－3－3＝2.
学生用书P119
命题点1 平面向量的数量积运算
例1 （1）[2023全国卷乙]正方形ABCD的边长是2，E是AB的中点，则EC·ED＝（ B ）
A.5B.3C.25D.5
解析 解法一 由题意知，EC＝EB＋BC＝12AB＋AD，ED＝EA＋AD＝－12AB＋AD，所以EC·ED＝（12AB＋AD）·（－12AB＋AD）＝｜AD｜2－14｜AB｜2，由题意知｜AD｜＝
｜AB｜＝2，所以EC·ED＝4－1＝3，故选B.
解法二 以点A为坐标原点，AB，AD的方向分别为x，y轴的正方向建立平面直角坐标系，则E（1，0），C（2，2），D（0，2），则EC＝（1，2），ED＝（－1，2），EC·ED＝－1＋4＝3，故选B.
（2）[2022全国卷甲]设向量a，b的夹角的余弦值为13，且｜a｜＝1，｜b｜＝3，则（2a＋b）·b＝ 11 .
解析 （2a＋b）·b＝2a·b＋b2＝2｜a｜｜b｜cs＜a，b＞＋｜b｜2＝2×1×3×13＋32＝11.
方法技巧
求非零向量a，b的数量积的方法
1.定义法：a·b＝｜a｜｜b｜cs θ.
2.基底法：选取合适的一组基底，利用平面向量基本定理将待求数量积的两个向量分别表示出来，进而根据数量积的运算律和定义求解.
3.坐标法：已知条件中有（或隐含）正交基底，优先考虑建立平面直角坐标系，利用a·b＝x1x2＋y1y2求解.
训练1 （1）[2022全国卷乙]已知向量a，b满足｜a｜＝1，｜b｜＝3，｜a－2b｜＝3，则a·b＝ （ C ）
A.－2B.－1C.1D.2
解析 由｜a－2b｜＝3，可得｜a－2b｜2＝a2－4a·b＋4b2＝9.
又｜a｜＝1，｜b｜＝3，所以a·b＝1，故选C.
（2）[全国卷Ⅱ]已知AB＝（2，3），AC＝（3，t），｜BC｜＝1，则AB·BC＝（ C ）
A.－3B.－2C.2D.3
解析 因为BC＝AC－AB＝（1，t－3），所以｜BC｜＝1+（t－3）2＝1，解得t＝3，所以BC＝（1，0），所以AB·BC＝2×1＋3×0＝2，故选C.
命题点2 平面向量数量积的应用
角度1 向量的模问题
例2 （1）[2022全国卷乙]已知向量a＝（2，1），b＝（－2，4），则｜a－b｜＝ （ D ）
A.2B.3C.4D.5
解析 由题意知a－b＝（2，1）－（－2，4）＝（4，－3），所以｜a－b｜＝42＋（－3）2＝5.故选D.
（2）[2023新高考卷Ⅱ]已知向量a，b满足｜a－b｜＝3，｜a＋b｜＝｜2a－b｜，则
｜b｜＝ 3 .
解析 由｜a－b｜＝3，得a2－2a·b＋b2＝3，即2a·b＝a2＋b2－3 ①.由｜a＋b｜＝
｜2a－b｜，得a2＋2a·b＋b2＝4a2－4a·b＋b2，整理得，a2＝2a·b，结合①，得a2＝a2＋b2－3，整理得，b2＝3，所以｜b｜＝3.
方法技巧
求平面向量模的两种方法
角度2 向量的夹角问题
例3 （1）[2023全国卷甲]已知向量a，b，c满足｜a｜＝｜b｜＝1，｜c｜＝2，且a＋b＋c＝0，则cs＜a－c，b－c＞＝（ D ）
A.－45B.－25C.25D.45
解析 ∵a＋b＋c＝0，∴c＝－a－b，等式两边同时平方得2＝a2＋b2＋2a·b＝1＋1＋2a·b，∴a·b＝0.
解法一 ∵a－c＝a－（－a－b）＝2a＋b，b－c＝b－（－a－b）＝a＋2b，∴（a－c）·（b－c）＝（2a＋b）·（a＋2b）＝2a2＋5a·b＋2b2＝4，且｜a－c｜＝｜2a＋b｜＝（2a＋b）2＝4+1＝5，｜b－c｜＝｜a＋2b｜＝（a+2b）2＝1+4＝5，
∴cs＜a－c，b－c＞＝（a－c）·（b－c）｜a－c｜·｜b－c｜＝45，故选D.
解法二 如图，令OA＝a，OB＝b，则OC＝c，∴CA＝a－c，CB＝b－c，而｜AB｜＝2，｜AC｜＝｜BC｜＝5，在△ABC中，由余弦定理得cs＜a－c，b－c＞＝cs＜CA，CB＞＝cs∠ACB＝5+5－225×5＝45，故选D.
解法三 如图，令向量a，b的起点均为O，终点分别为A，B，以OA，OB的方向分别为x，y轴的正方向建立平面直角坐标系，则a＝（1，0），b＝（0，1），c＝－a－b＝
（－1，－1），所以a－c＝（2，1），b－c＝（1，2），则cs＜a－c，b－c＞＝（a－c）·（b－c）｜a－c｜·｜b－c｜＝2+25×5＝45，故选D.
（2）[2022新高考卷Ⅱ]已知向量a＝（3，4），b＝（1，0），c＝a＋tb，若＜a，c＞＝
＜b，c＞，则t＝（ C ）
A.－6B.－5C.5D.6
解析 解法一 由题意，得c＝a＋tb＝（3＋t，4），所以a·c＝3×（3＋t）＋4×4＝25＋3t，b·c＝1×（3＋t）＋0×4＝3＋t.因为＜a，c＞＝＜b，c＞，所以cs＜a，c＞＝cs＜b，
c＞，即a·c｜a||c｜＝b·c｜b||c｜，即25+3t5＝3＋t，解得t＝5.故选C.
解法二 因为＜a，c＞＝＜b，c＞，且c＝a＋tb，所以由向量加法的平行四边形法则得｜a｜＝t｜b｜，易知｜a｜＝5，｜b｜＝1，所以t＝5.
方法技巧
求平面向量夹角问题的三种方法
角度3 向量的垂直问题
例4 （1）[2023新高考卷Ⅰ]已知向量a＝（1，1），b＝（1，－1）.若（a＋λb）⊥（a＋μb），则（ D ）
A.λ＋μ＝1B.λ＋μ＝－1
C.λμ＝1 D.λμ＝－1
解析 因为a＝（1，1），b＝（1，－1），所以a＋λb＝（1＋λ，1－λ），a＋μb＝（1＋μ，1－μ），因为（a＋λb）⊥（a＋μb），所以（a＋λb）·（a＋μb）＝0，所以（1＋λ）（1＋μ）＋（1－λ）（1－μ）＝0，整理得λμ＝－1.故选D.
（2）[全国卷Ⅱ]已知单位向量a，b的夹角为60°，则在下列向量中，与b垂直的是（ D ）
A.a＋2bB.2a＋bC.a－2bD.2a－b
解析 解法一 由题意，得a·b＝｜a｜｜b｜cs 60°＝12.对于A，（a＋2b）·b＝a·b＋2b2＝12＋2＝52≠0，故A不符合题意；对于B，（2a＋b）·b＝2a·b＋b2＝1＋1＝2≠0，故B不符合题意；对于C，（a－2b）·b＝a·b－2b2＝12－2＝－32≠0，故C不符合题意；对于D，（2a－b）·b＝2a·b－b2＝1－1＝0，所以（2a－b）⊥b，符合题意.故选D.
解法二 根据条件，分别作出向量b与A，B，C，D四个选项对应的向量的位置关系，如图所示.
A B C D
由图易知，只有选项D满足题意.故选D.
解法三 不妨设a＝（12，32），b＝（1，0），则a＋2b＝（52，32）， 2a＋b＝（2，3），a－2b＝（－32，32），2a－b＝（0，3），易知，只有（2a－b）·b＝0，即（2a－b）⊥b.故选D.
方法技巧
1.证明两个向量垂直的解题策略
先计算出这两个向量的坐标或表示出两个向量，然后根据数量积的运算公式，计算出这两个向量的数量积为0即可.
2.已知两个向量的垂直关系，求解相关参数的值
根据两个向量垂直的充要条件，列出相应的关系式，进而求解参数.
训练2 （1）[2023广州市二检]已知两个非零向量a，b满足｜a｜＝3｜b｜，（a＋b）⊥b，则cs 〈a，b〉＝（ D ）
A.12B.－12C.13D.－13
解析 因为（a＋b）⊥b，所以（a＋b）·b＝0，即a·b＝－b2，所以｜a｜·｜b｜·cs 〈a，b〉＝－｜b｜2，即3｜b｜·｜b｜cs 〈a，b〉＝－｜b｜2，则cs 〈a，b〉＝－13.故选D.
（2）[2021全国卷甲]若向量a，b满足｜a｜＝3，｜a－b｜＝5，a·b＝1，则｜b｜＝ 32 .
解析 由｜a－b｜＝5得（a－b）2＝25，即a2－2a·b＋b2＝25，结合｜a｜＝3，a·b＝1，得32－2×1＋｜b｜2＝25，所以｜b｜＝32.
命题点3 平面向量的应用
例5 在日常生活中，我们会看到两人共提一个行李包的情况（如图）.假设行李包所受重力为G，所受的两个拉力分别为F1，F2.若｜F1｜＝
｜F2｜，F1与F2的夹角为θ，则下列结论不正确的是（ D ）
A.｜F1｜的最小值为12｜G｜
B.当θ＝2π3时，｜F1｜＝｜G｜
C.当θ＝π2时，｜F1｜＝22｜G｜
D.当θ＝2π3时，F1在F2方向上的投影数量为｜G｜2
解析 由题意知，｜G｜＝｜F1＋F2｜，且｜G｜为定值，因为｜F1｜＝｜F2｜，所以
｜G｜2＝｜F1｜2＋｜F2｜2＋2｜F1｜｜F2｜·cs θ＝2｜F1｜2（1＋cs θ），所以｜F1｜2＝｜G｜22（1+csθ）.
当θ∈（0，π）时，y＝cs θ单调递减，
所以关于θ的函数y＝｜F1｜2＝｜G｜22（1+csθ）单调递增，
即θ越大越费力，θ越小越省力.
当θ＝0时，｜F1｜min＝12｜G｜；
当θ＝π2时，｜F1｜＝22｜G｜；
当θ＝2π3时，｜F1｜＝｜G｜.故A，B，C正确.
对于D选项，当θ＝2π3时，F1在F2方向上的投影数量为｜F1｜cs 2π3＝｜G｜cs2π3＝
－｜G｜2，故D不正确.故选D.
方法技巧
用向量方法解决实际问题的步骤
训练3 一条东西方向的河流两岸平行，河宽2503 m，河水的速度为正东3 km/h.一艘小货船准备从河流南岸码头P处出发，航行到河流对岸对应点Q（PQ与河流的方向垂直）的正西方向并且与Q相距250 m的码头M处卸货，若水流的速度与小货船航行的速度的合速度的大小为 5 km/h，则当小货船的航程最短时，小货船航行速度的大小为（ C ）
A.33 km/hB.6 km/h
C.7 km/hD.36 km/h
解析 连接PM，由题意得，当小货船的航程最短时，其航线为线段PM.
设小货船航行的速度为v，水流的速度为v1，水流的速度与小货船航行的速度的合速度为v2，作出示意图，如图所示.
PQ＝2503 m，QM＝250 m.
在Rt△PQM中，（根据“PQ与河流的方向垂直”得到△PMQ的形状）
tan∠PMQ＝PQQM＝2503250＝3，由题意∠PMQ∈（0，π2），
所以∠PMQ＝π3，∠MPQ＝π6，＜v1，v2＞＝π2＋π6＝2π3，
易知v＝v2－v1，｜v1｜＝3，｜v2｜＝5，
所以｜v｜＝（v2－v1）2＝｜v2｜2＋｜v1｜2－2v1·v2＝52＋32－2×5×3cs2π3＝7，
所以小货船航行速度的大小为7 km/h，故选C.
学生用书P120
极化恒等式
例6 （1）[2022北京高考]在△ABC中，AC＝3，BC＝4，∠C＝90°.P为△ABC所在平面内的动点，且PC＝1，则PA·PB的取值范围是（ D ）
A.[－5， 3]B.[－3，5]C.[－6，4]D.[－4，6]
解析 解法一（极化恒等式） 设AB的中点为M，CM与CP的夹角为θ，由极化恒等式得PA·PB＝PM2－14AB 2＝（CM－CP）2－254＝CM2＋CP2－2CM·CPcs θ－254＝254＋1－5cs θ－254＝1－5cs θ，因为cs θ∈[－1，1]，所以PA·PB∈[－4，6].
解法二 以C为坐标原点，CA，CB所在直线分别为x轴，y轴建立平面直角坐标系，则
A（3，0），B（0，4），设P（x，y），则x2＋y2＝1，PA＝（3－x，－y），PB＝
（－x，4－y），所以PA·PB＝x2－3x＋y2－4y＝（x－32）2＋（y－2）2－254，又（x－32）2＋（y－2）2表示圆x2＋y2＝1上一点到点（32，2）距离的平方，圆心（0，0）到点（32，2）的距离为52，所以PA·PB∈[（52－1）2－254，（52＋1）2－254]，即PA·PB∈[－4，6]，故选D.
解法三 以C为坐标原点，CA，CB所在直线分别为x轴，y轴建立平面直角坐标系，则
A（3，0），B（0，4），因为PC＝1，所以P在以（0，0）为圆心，1为半径的圆上，所以设点P坐标为（cs α，sin α），则PA·PB＝（3－cs α，－sin α）·（－cs α，4－sin α）＝1－3cs α－4sin α＝1－5sin（α＋φ）（其中tan φ＝34）.因为sin（α＋φ）∈[－1，1]，所以PA·PB∈[－4，6].
（2）[全国卷Ⅱ]已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则PA·（PB＋PC）的最小值是（ B ）
A.－2B.－32C.－43D.－1
解析 解法一 如图，取BC的中点D，则PB＋PC＝2PD，则PA·（PB＋PC）＝2PA·PD.在△PAD中，取AD的中点O，则2PA·PD＝2｜PO｜2－12｜AD｜2＝2｜PO｜2－32.
由于点P在平面内是任意的，因此当且仅当点P，O重合时，｜PO｜取得最小值，即2PA·PD取得最小值－32.故选B.
解法二 如图，以等边三角形ABC的底边BC的中点O为坐标原点，BC所在直线为x轴，BC的垂直平分线为y轴建立平面直角坐标系，则A（0，3），B（－1，0），C（1，0）.
设P（x，y），则PA＝（－x，3－y），PB＝（－1－x，－y），PC＝（1－x，－y），所以PA·（PB＋PC） ＝（－x，3－y）·（－2x，－2y）＝2x2＋2（y－32）2－32，易知当x＝0，y＝32时，PA·（PB＋PC）取得最小值，最小值为－32.故选B.
方法技巧
极化恒等式：a·b＝14[（a＋b）2－（a－b）2].
几何意义：向量a，b的数量积等于以这组向量所对应的线段为邻边的平行四边形的“和对角线长”与“差对角线长”的平方差的14.
应用：（1）在▱ABCD中，O为AC，BD的交点，则有AB·AD＝14（4｜AO｜2－4｜OB｜2）＝｜AO｜2－｜OB｜2.
（2）如图，在△ABC中，若M是BC的中点，则AB·AC＝AM2－14BC2.
训练4 [2023山东青岛二中5月模拟]如图，在四边形ABCD中，∠B＝60°，AB＝3，BC＝6，且AD＝λBC，AD·AB＝－32，则实数λ的值为 16 ，若M，N是线段BC上的动点，且
｜MN｜＝1，则DM·DN的最小值为 132 .
解析 依题意得AD∥BC，∠BAD＝120°，由AD·AB＝｜AD｜·｜AB｜·cs∠BAD＝
－32｜AD｜＝－32，得｜AD｜＝1，因此λ＝｜AD｜｜BC｜＝16.取MN的中点E，连接DE，则DM＋DN＝2DE，DM·DN＝14[（DM＋DN）2－（DM－DN）2]＝DE2－14NM2＝DE2－14.注意到线段MN在线段BC上运动时，DE的最小值等于点D到直线BC的距离，即AB·sin B＝332，因此DE2－14的最小值为（332）2－14＝132，即DM·DN的最小值为132.
思维帮·提升思维 快速解题
三角形“四心”的向量表示与运用
角度1 垂心的向量表示与运用
例7 [2023山西朔州模拟]已知H为△ABC的垂心，若AH＝13AB＋25AC，则sin∠BAC＝ 63 .
解析 如图，连接BH，CH，因为AH＝13AB＋25AC，所以BH＝BA＋AH＝
－23AB＋25AC，CH＝CA＋AH＝13AB－35AC.由H为△ABC的垂心，得BH·AC＝0，即（－23AB＋25AC）·AC＝0，可知25｜AC｜2＝23｜AC｜·｜AB｜cs∠BAC，即cs∠BAC＝3｜AC｜5｜AB｜ ①，同理有CH·AB＝0，即（13AB－35AC）·AB＝0，可知13｜AB｜2＝35｜AC｜｜AB｜cs∠BAC，即cs∠BAC＝5｜AB｜9｜AC｜ ②，①×②得cs2∠BAC＝13，得sin2∠BAC＝1－cs2∠BAC＝1－13＝23，又sin∠BAC＞0，所以sin∠BAC＝63.
方法技巧
1.垂心的定义：三角形三条高的交点称为该三角形的垂心.
2.垂心的性质：设O是△ABC的垂心，P为△ABC所在平面内任意一点，则有（1）OA·OB＝OB·OC＝OC·OA；
（2）｜OA｜2＋｜BC｜2＝｜OB｜2＋｜CA｜2＝｜OC｜2＋｜AB｜2；
（3）动点P满足AP＝λ（AB｜AB｜cs∠ABC＋AC｜AC｜cs∠ACB）或OP＝OA＋λ（AB｜AB｜cs∠ABC＋AC｜AC｜cs∠ACB），λ∈R时，动点P的轨迹经过△ABC的垂心.
角度2 重心的向量表示与运用
例8 [2023广州一中诊断]如图，已知点G是△ABC的重心，过G作直线与AB，AC分别交于M，N两点，AM＝xAB，AN＝yAC，则xyx＋y＝ 13 .
解析 由M，G，N三点共线得，存在实数λ使得AG＝λAM＋（1－λ）AN＝xλAB＋y（1－λ）AC，且0＜λ＜1.
因为G是△ABC的重心，所以AG＝13（AB＋AC），所以xλ＝13，y（1－λ）＝13，则x＝13λ，y＝13（1－λ），故xy＝19λ（1－λ），x＋y＝13λ（1－λ），则xyx＋y＝19λ（1－λ）×3λ（1－λ）＝13.
方法技巧
1.重心的定义：三角形三条中线的交点称为该三角形的重心.
2.重心的性质：设O是△ABC的重心，P为平面内任意一点，则有（1）OA＋OB＋OC＝0；（2）PO＝13（PA＋PB＋PC）；（3）动点P满足AP＝λ（AB＋AC）或OP＝OA＋
λ（AB＋AC），λ∈[0，＋∞）时，动点P的轨迹经过△ABC的重心.
角度3 外心的向量表示与运用
例9 [2023湖北荆门模拟]已知点O为△ABC所在平面内一点，在△ABC中，满足2AB·AO＝｜AB｜2，2AC·AO＝｜AC｜2，则点O为该三角形的（ B ）
A.内心B.外心C.垂心D.重心
解析 因为2AB·AO＝2｜AB｜｜AO｜cs∠OAB＝｜AB｜2，所以｜AO｜cs∠OAB＝
12｜AB｜，则向量AO在向量AB上的投影向量的长度为｜AB｜的一半，所以点O在边AB的中垂线上，同理，点O在边AC的中垂线上，所以点O为该三角形的外心，故选B.
方法技巧
1.外心的定义：三角形三边垂直平分线的交点称为该三角形的外心.
2.外心的性质：若O是△ABC的外心，则有（1）｜OA｜＝｜OB｜＝｜OC｜；
（2）（OA＋OB）·AB＝（OA＋OC）·AC＝（OB＋OC）·BC＝0.
角度4 内心的向量表示与运用
例10 [2023四川南充阶段测试]已知O是△ABC所在平面内一点，且点O满足OA·（AB｜AB｜－AC｜AC｜）＝OB·（BA｜BA｜－BC｜BC｜）＝OC·（CA｜CA｜－CB｜CB｜）＝0，则点O为△ABC的（ C ）
A.外心B.重心C.内心D.垂心
解析 解法一 AB｜AB｜，AC｜AC｜分别是与AB，AC方向相同的单位向量，可令AB｜AB｜＝AD，AC｜AC｜＝AE，连接ED，则△ADE为腰长是1的等腰三角形，AB｜AB｜－AC｜AC｜＝ED，所以OA·ED＝0，所以AO为∠CAB的平分线，同理BO为∠ABC的平分线，CO为∠ACB的平分线，所以O为△ABC的内心.故选C.
解法二 OA·（AB｜AB｜－AC｜AC｜）＝0，即OA·AB｜AB｜＝OA·AC｜AC｜，即｜OA｜·｜AB｜｜AB｜cs（π－∠OAB）＝｜OA｜·｜AC｜｜AC｜·cs（π－∠OAC），所以∠OAB＝∠OAC，即AO是∠BAC的平分线，同理可得BO为∠ABC的平分线，CO为∠ACB的平分线，所以O为△ABC的内心.
方法技巧
1.内心的定义：三角形三条内角平分线的交点称为该三角形的内心.
2.内心的性质：若O是△ABC的内心，P为平面内任意一点，则有（1）aOA＋bOB＋cOC＝0（a，b，c分别是△ABC的三边BC，AC，AB的长）；（2）动点P满足AP＝λ（AB｜AB｜＋AC｜AC｜）或OP＝OA＋λ（AB｜AB｜＋AC｜AC｜），λ∈[0，＋∞）时，动点P的轨迹经过△ABC的内心.
训练5 （1）[2023长春模拟]点O是平面α上一定点，点P是平面α上一动点，A，B，C是平面α上△ABC的三个顶点（点O，P，A，B，C均不重合），以下命题正确的是 ①②③④ .
①动点P满足OP＝OA＋PB＋PC，则△ABC的重心一定在满足条件的P点的集合中；
②动点P满足OP＝OA＋λ（AB｜AB｜＋AC｜AC｜）（λ＞0），则△ABC的内心一定在满足条件的P点的集合中；
③动点P满足OP＝OA＋λ（AB｜AB｜sinB＋AC｜AC｜sinC）（λ＞0），则△ABC的重心一定在满足条件的P点的集合中；
④动点P满足OP＝OA＋λ（AB｜AB｜csB＋AC｜AC｜csC）
（λ∈R），则△ABC的垂心一定在满足条件的P点的集合中.
解析 对于①，OP＝OA＋PB＋PC，移项得－OA＋OP＝AP＝PB＋PC，即PA＋PB＋PC＝0，则点P是△ABC的重心，故①正确.
对于②，因为动点P满足OP＝OA＋λ（AB｜AB｜＋AC｜AC｜）（λ＞0），移项得AP＝λ（AB｜AB｜＋AC｜AC｜）（λ＞0），所以AP与∠BAC的平分线对应的向量共线，所以P在∠BAC的平分线上，所以△ABC的内心在满足条件的P点的集合中，②正确.
对于③，OP＝OA＋λ（AB｜AB｜sinB＋AC｜AC｜sinC）（λ＞0），即AP＝λ（AB｜AB｜sinB＋AC｜AC｜sinC），过点A作AD⊥BC，垂足为D，则｜AB｜sin B＝｜AC｜sin C＝AD，AP＝λAD（AB＋AC），设M为BC的中点，则AB＋AC＝2AM，则AP＝2λADAM，所以P在BC的中线上，所以△ABC的重心一定在满足条件的P点的集合中，③正确.
对于④，OP＝OA＋λ（AB｜AB｜csB＋AC｜AC｜csC）（λ∈R），即AP＝λ（AB｜AB｜csB＋AC｜AC｜csC），所以AP·BC＝λ（AB·BC｜AB｜csB＋AC·BC｜AC｜csC）＝λ（－｜BC｜＋｜BC｜）＝0，所以AP⊥BC，所以P在边BC上的高所在的直线上，所以△ABC的垂心一定在满足条件的P点的集合中，④正确.故正确的命题是①②③④.
（2）[多选/2023安徽淮北师大附中模拟]数学家欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理：三角形的重心、垂心和外心共线.这条线就是三角形的欧拉线.在△ABC中，O，H，G分别是外心、垂心和重心，D为BC边的中点，则下列四个选项中正确的是（ ABD ）
A.GH＝2OGB.GA＋GB＋GC＝0
C.AH＝ODD.S△ABG＝S△BCG＝S△ACG
解析 根据题意画出图形，如图所示.
对于B，连接GD，由重心的性质可得G为AD的三等分点，且GA＝－2GD，又D为BC的中点，所以GB＋GC＝2GD，所以GA＋GB＋GC＝－2GD＋2GD＝0，故B正确.
对于A，C，因为O为△ABC的外心，D为BC的中点，所以OD⊥BC，所以AH∥OD，所以△AHG∽△DOG，所以GHOG＝AHOD＝AGDG＝2，即GH＝2OG，AH＝2OD，故A正确，C不正确.
对于D，延长AH交BC于N，过点G作GE⊥BC，垂足为E，则△DEG∽△DNA，所以GEAN＝DGDA＝13，所以S△BGC＝12×BC×GE＝12×BC×13×AN＝13S△ABC，同理，S△AGC＝S△AGB＝13S△ABC，所以S△ABG＝S△BCG＝S△ACG，故D正确.故选ABD.
1.[命题点2/多选]已知e1，e2是单位向量，且e1·e2＝12，若向量a满足e1·a＝2，则下列选项正确的是（ ABD ）
A.｜e1－e2｜＝1
B.e1在e2上的投影向量的模为12
C.e1与e1－e2的夹角为5π12
D.a在e1上的投影向量为2e1
解析 ｜e1－e2｜2＝e12－2e1·e2＋e22＝1，故｜e1－e2｜＝1，故A正确.
因为e1在e2上的投影向量为e1·e2｜e2｜e2＝12e2，所以e1在e2上的投影向量的模为12，故B正确.
因为e1·（e1－e2）＝1×1×cs＜e1，e1－e2＞＝e12－e1·e2＝12，所以＜e1，e1－e2＞＝π3，故C错误.
设e1与a的夹角为θ，因为e1·a＝2＝｜a｜cs θ，所以a在e1上的投影向量为
（｜a｜cs θ）e1＝2e1，故D正确.
2.[命题点2/2022天津高考]在△ABC中，CA＝a，CB＝b，AC＝2DC，CB＝2BE，用a，b表示向量DE，则DE＝ 32b－12a ；若AB⊥DE，则∠ACB的最大值为 π6 .
解析 由题意知CD＝12CA＝12a，又CB＝2BE，所以CE＝32CB＝32b，则DE＝CE－CD＝32b－12a.
因为AB⊥DE，AB＝CB－CA＝b－a，
所以AB·DE＝（b－a）·（32b－12a）＝0，化简整理，得3b2＋a2－4a·b＝0，则3｜b｜2＋
｜a｜2－4｜a｜｜b｜·cs∠ACB＝0，所以cs∠ACB＝3｜b｜2＋｜a｜24｜a||b｜≥23｜a||b｜4｜a||b｜＝32，当且仅当｜a｜＝3｜b｜时等号成立，又∠ACB∈（0，π），所以∠ACB≤π6，即∠ACB的最大值为π6.
3.[思维帮]在△ABC中，∠C＝90°，AC＝4，BC＝3，D是AB的中点，E，F分别是边BC，AC上的动点，且EF＝1，则DE·DF的最小值为 154 .
解析 如图，取EF的中点H，连接DH，CH，CD，则CD＝12AB＝52，CH＝12EF＝12，DE·DF＝DH2－EF24＝DH2－14，因为｜CH｜＋
｜DH｜≥｜CD｜，所以｜DH｜≥｜CD｜－｜CH｜＝52－12＝2，所以DE·DF≥4－14＝154.
学生用书·练习帮P318
1.[2024武汉部分学校调考]两个单位向量e1与e2满足e1·e2＝0，则向量e1－3e2与e2的夹角为（ D ）
A.30°B.60°
C.120°D.150°
解析 解法一 因为e1，e2是单位向量，所以｜e1｜＝｜e2｜＝1，又e1·e2＝0，所以（e1－3e2）·e2＝e1·e2－3e22＝－3，（e1－3e2）2＝e12－23e1·e2＋3e22＝1＋3＝4，所以｜e1－3e2｜＝2.设e1－3e2与e2的夹角为θ，则cs θ＝（e1－3e2）·e2｜e1－3e2｜·｜e2｜＝－32，因为0°≤θ≤180°，所以θ＝150°.故选D.
解法二 因为e1，e2是单位向量，e1·e2＝0，所以不妨设e1＝（1，0），e2＝（0，1），所以e1－3e2＝（1，0）－3（0，1）＝（1，－3）.设e1－3e2与e2的夹角为θ，则cs θ＝（e1－3e2）·e2｜e1－3e2｜·｜e2｜＝（1，－3）·（0，1）12＋（－3）2×1＝－32，因为0°≤θ≤180°，所以θ＝150°.故选D.
2.[2024安徽六校联考]已知向量m，n，且｜m｜＝｜n｜＝1，｜3m－2n｜＝7，则向量m在向量n上的投影向量为（ C ）
A.0B.12mC.12nD.－12n
解析 由｜3m－2n｜＝7，得｜3m－2n｜2＝（3m－2n）2＝9m2＋4n2－12m·n＝7，又
｜m｜＝｜n｜＝1，所以9＋4－12m·n＝7，整理得m·n＝12，因为＜m，n＞∈[0，π]，所以m，n的夹角为π3，所以向量m在向量n上的投影向量为12n.故选C.
3.[2023吉林长春质监]已知向量a与b的夹角为60°，｜a｜＝2，｜b｜＝1，则｜a－2b｜＝（ C ）
A.1B.3C.2D.23
解析解法一 a·b＝｜a｜·｜b｜cs 60°＝2×1×12＝1，所以｜a－2b｜2＝a2－4a·b＋4b2＝4－4×1＋4＝4，所以｜a－2b｜＝2，故选C.
解法二 如图所示，记OA＝a，OB＝b，则∠AOB＝60°.延长OB到C，使OC＝2OB＝2b，因为｜a｜＝2，｜b｜＝1，所以｜OA｜＝｜OC｜＝2.连接AC，则△OAC为正三角形，所以｜a－2b｜＝｜CA｜＝2，故选C.
4.已知单位向量a，b满足｜a＋b｜＞1，则a与b夹角的取值范围是（ B ）
A.[0，π3）B.[0，2π3）C.（π3，π]D.（2π3，π]
解析 解法一 设单位向量a，b的夹角为θ，则θ∈[0，π]，将｜a＋b｜＞1两边同时平方得a2＋2a·b＋b2＞1，化简得2＋2cs θ＞1，即cs θ＞－12，又因为θ∈[0，π]，所以0≤θ＜2π3，故选B.
解法二 设单位向量a，b的夹角为θ，显然当θ＝0时，｜a＋b｜＞1成立；当θ≠0时，如图所示，令OA＝a，OB＝b，以OA，OB为邻边作平行四边形OACB，则OC＝a＋b，设∠AOB＝θ，因为a，b均为单位向量，所以平行四边形OACB是边长为1的菱形，在θ从0增大到π的过程中，｜OC｜一直在减小，当｜OC｜＝1时，△AOC为等边三角形，此时θ＝2π3，故0＜θ＜2π3.综上可知，0≤θ＜2π3，故选B.
5.[2023河南安阳模拟]已知a＝（1，0），b＝（0，1），c＝a＋tb，t∈R，若sin＜a，c＞＝sin＜b，c＞，则t＝（ B ）
A.－1B.±1C.2D.±2
解析 ∵a＝（1，0），b＝（0，1），c＝a＋tb，∴c＝（1，t），又sin＜a，c＞＝
sin＜b，c＞，∴cs＜a，c＞＝±cs＜b，c＞，而cs＜a，c＞＝11+t2，cs＜b，c＞＝t1+t2，∴1＝±t，即t＝±1，故选B.
6.[多选]已知向量a＝（1，sin θ），b＝（cs θ，2），则下列命题正确的是（ BD ）
A.存在θ，使得a∥b
B.当tan θ＝－22时，a与b垂直
C.对任意θ，都有｜a｜≠｜b｜
D.当a·b＝－3时，a在b上的投影向量的模为377
解析 对于A选项，若a∥b，则1×2－sin θcs θ＝0，又因为sin θcs θ＝12sin 2θ∈[－12，12]，所以方程1×2－sin θcs θ＝0无解，即不存在θ，使得a∥b，所以A不正确；对于B选项，若a⊥b，则cs θ＋2sin θ＝0，即tan θ＝－22，所以B正确；
对于C选项，｜a｜＝1+sin2θ，｜b｜＝2+cs2θ，当θ＝π2时，｜a｜＝｜b｜＝2，所以C不正确；
对于D选项，a·b＝cs θ＋2sin θ＝3sin（θ＋φ）＝－3，其中sin φ＝33，cs φ＝63，所以θ＋φ＝2kπ－π2，k∈Z，所以｜b｜＝2+cs2θ＝2+13＝73，a在b上的投影向量的模为｜a·b｜b｜×a｜a｜｜＝｜－373×a｜a｜｜＝377，所以D正确.故选BD.
7.已知向量a与b的夹角为π3，且｜a｜＝1，｜2a－b｜＝3，则｜b｜＝ 1 .
解析 ｜2a－b｜2＝（2a－b）2＝4｜a｜2－4｜a｜·｜b｜cs＜a，b＞＋｜b｜2＝4－2｜b｜＋｜b｜2＝3，解得｜b｜＝1.
8.已知非零向量m，n满足4｜m｜＝3｜n｜，cs＜m，n＞＝13.若n⊥（tm＋n），则t＝ －4 .
解析 由n⊥（tm＋n）可得n·（tm＋n）＝0，即tm·n＋n2＝0，所以t＝－n2m·n＝
－n2｜m｜·｜n｜cs＜m，n＞＝－｜n｜2｜m｜×｜n｜×13＝－3×｜n｜｜m｜＝－3×43＝－4.
9.[2021新高考卷Ⅱ]已知向量a＋b＋c＝0，｜a｜＝1，｜b｜＝｜c｜＝2，a·b＋b·c＋c·a＝ －92 .
解析 （a＋b＋c）2＝a2＋b2＋c2＋2（a·b＋a·c＋b·c）＝0，因为｜a｜＝1，｜b｜＝｜c｜＝2，所以a·b＋a·c＋b·c＝－92.
10.已知单位向量a，b满足｜a－2b｜＝3a·b，则向量a，b夹角的余弦值为 59 .
解析 设a，b的夹角为θ，将｜a－2b｜＝3a·b两边同时平方得9cs2θ＋4cs θ－5＝0，解得cs θ＝59或cs θ＝－1.由｜a－2b｜＝3a·b可知a·b≥0，所以cs θ≥0，所以cs θ＝59.
11.[2024山东日照联考]如图，在边长为2的等边△ABC中，点E为中线BD的三等分点（靠近点B），点F为BC的中点，则FE·FC＝（ B ）
A.－34B.－12
C.34D.12
解析 解法一 由题意，以点D为坐标原点，DA，DB的方向分别为x，y轴的正方向，建立平面直角坐标系，则D（0，0），C（－1，0），B（0，3），E（0，233），F（－12，32），则FE＝（12，36），FC＝（－12，－32），∴FE·FC＝12×（－12）＋36×（－32）＝
－12，故选B.
解法二 ∵FC＝12BC，FE＝BE－BF＝13BD－12BC＝16（BA＋BC）－12BC＝16BA－13BC，∴FE·FC＝12BC·（16BA－13BC）＝112BC·BA－16BC2＝112×2×2×csπ3－16×22＝－12，故选B.
12.[角度创新]已知向量a＝（1，2），b＝（－k2，1），k∈R，a，b的夹角为θ，若存在实数m，使得｜b｜cs θ－5m＞0，则m的取值范围是（ C ）
A.（－12，＋∞）B.（0，＋∞）
C.（－∞，25）D.（－∞，12）
解析 由｜b｜cs θ－5m＞0，得m＜55｜b｜cs θ，又因为｜a｜＝5，所以m＜｜a||b｜csθ5.若存在实数m，使得｜b｜cs θ－5m＞0，则m＜（a·b5）max.因为a·b＝－k2＋2，所以（a·b）max＝2，故m＜25，故选C.
13.如图，△ABC中，AB＝AC＝4，∠BAC＝2π3，半径为1的☉A分别交AB，AC于点E，F，点P是劣弧EF上的一个动点，则PB·PC的取值范围是 [－11，－9] .
解析 解法一（坐标法） 如图1，以A为原点，垂直于BC的直线为x轴建立平面直角坐标系xAy，则B（2，－23），C（2，23），
设P（cs θ，sin θ），其中θ∈[－π3，π3].
所以PB·PC＝（2－cs θ，－23－sin θ）·（2－cs θ，23－sin θ）＝（2－cs θ）2＋sin2θ－12＝－7－4cs θ. 图1
因为cs θ∈[12，1]，
所以PB·PC∈[－11，－9].
解法二（几何法） 如图2，取BC的中点M，连接PM，则PB·PC＝PM2－MC2.
因为MC为定值，所以PB·PC的变化可由｜PM｜的变化确定. 图2
连接AM，易得AM＝2，MC＝23，当P为劣弧EF与AM的交点时，PM取得最小值，为AM－1＝1.连接EM，PM的最大值为EM＝BE2＋BM2－2·BE·BM·cs∠EBM＝3.
所以PM2－MC2的取值范围是[－11，－9]，即PB·PC∈[－11，－9].
14.[2024广东七校联考]已知点D在线段AB上，CD是△ABC的一条角平分线，E为CD上一点，且满足BE＝BA＋λ（AD｜AD｜＋AC｜AC｜）（λ＞0），｜CA｜－｜CB｜＝6，｜BA｜＝14，设BA＝a，则BE在a上的投影向量为 27a .（结果用带a的式子表示）
解析 如图，连接AE，因为CD是△ABC的一条角平分线，且BE－BA＝AE＝λ（AD｜AD｜＋AC｜AC｜）（λ＞0），所以AE也是△ABC的一条角平分线，所以E为△ABC的内心.作△ABC的内切圆，切点分别为M，Q，N，并连接EM，EQ，EN，则由内切圆的性质可得，｜AC｜－｜BC｜＝｜AM｜－
｜BN｜＝｜AQ｜－｜BQ｜＝6，又｜AQ｜＋｜BQ｜＝14，所以｜BQ｜＝7－3＝4，所以BE在a上的投影向量的模为4，则BE在a上的投影向量为414a＝27a.
15.骑行是一种能有效改善心肺功能的耐力性有氧运动，深受大众喜爱.如图是某一自行车的平面结构示意图，已知图中的圆A（前轮），圆D（后轮）的半径均为3，△ABE，△BEC，△ECD均是边长为4的等边三角形.设P为后轮上一点，则在骑行该自行车的过程中，AC·CP达到最大值时，点P到地面的距离为（ B ）
A.32B.332
C.32＋3D.62＋3
解析 如图，以D为坐标原点，AD所在直线为x轴建立平面直角坐标系，则A（－8，0），C（－2，23），圆D的方程为x2＋y2＝3.所以可设P（3cs α，3sin α），0≤α＜2π，所以AC＝（6，23），CP＝（3cs α＋2，3sin α－23），所以AC·CP＝63cs α＋12＋6sin α－12＝63cs α＋6sin α＝12sin（α＋π3），当α＋π3＝π2，即α＝π6时，AC·CP取得最大值，此时点P（32，32），点P到地面的距离为32＋3＝332，故选B.课标要求
命题点
五年考情
命题分析预测
1.理解平面向量数量积的概念及其物理意义，会计算平面向量的数量积.
2.了解平面向量投影的概念以及投影向量的意义.
3.会用数量积判断两个平面向量的垂直关系.
4.能用坐标表示平面向量的数量积，会表示两个平面向量的夹角.
5.会用向量方法解决简单的平面几何问题、力学问题以及其他实际问题，体会向量在解决数学和实际问题中的应用.
平面向量的数量积运算
2023全国卷乙T6；2022全国卷乙T3；2022全国卷甲T13；2021新高考卷ⅡT15；2020北京T13；2019全国卷ⅡT3
本讲每年必考，主要考查向量的数量积运算、向量的夹角、模长、垂直问题，一般以客观题形式出现，难度不大.预计2025年高考命题稳定，常规备考的同时要关注向量与三角、解析几何等的综合以及坐标法在解题中的应用.
平面向量数量积的应用
2023新高考卷ⅠT3；2023新高考卷ⅡT13；2023全国卷甲T4；2022全国卷乙T3；2022新高考卷ⅡT4；2022天津T14；2021新高考卷ⅠT10；2021全国卷甲T14；2021全国卷甲T14；2021全国卷乙T14；2020全国卷ⅠT14；2020全国卷ⅡT13；2020新高考卷ⅠT7；2019全国卷ⅠT7
平面向量的应用
2023全国卷乙T12；2020天津T15
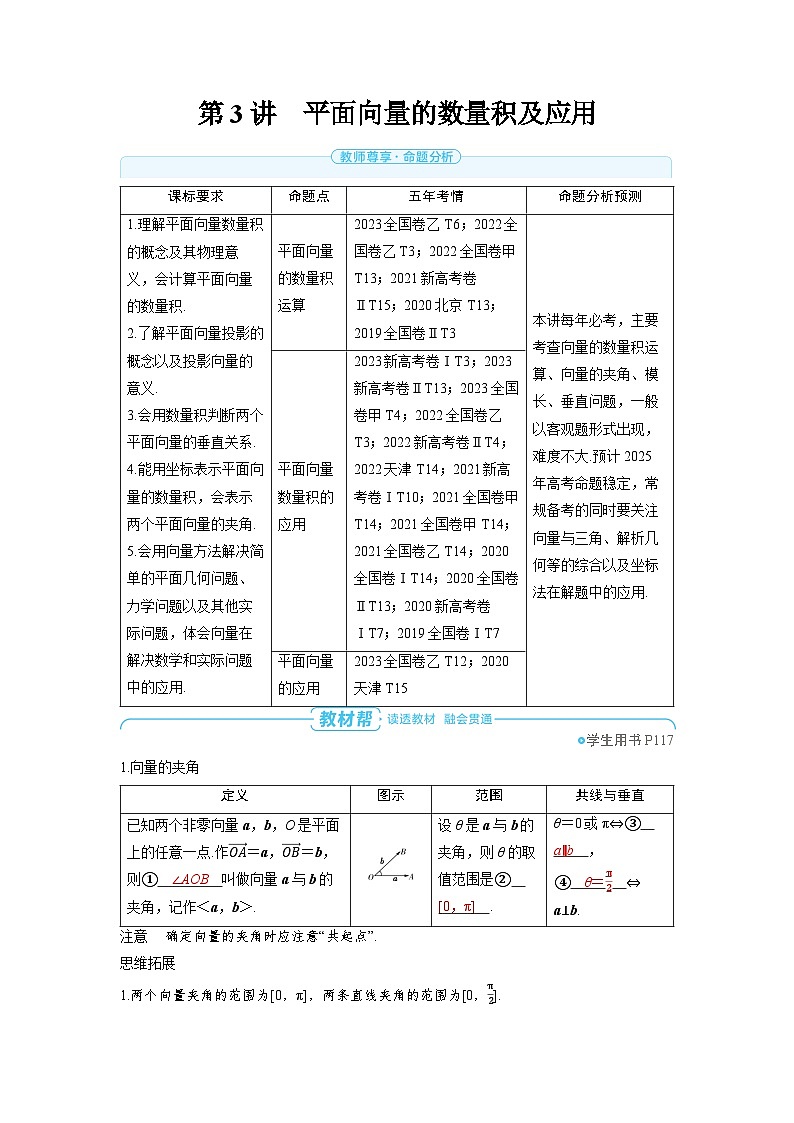
定义
图示
范围
共线与垂直
已知两个非零向量a，b，O是平面上的任意一点.作OA＝a，OB＝b，则① ∠AOB 叫做向量a与b的夹角，记作＜a，b＞.
设θ是a与b的夹角，则θ的取值范围是② [0，π] .
θ＝0或π⇔③ a∥b ，
④ θ＝π2 ⇔ a⊥b.
几何表示
坐标表示
数量积
a·b＝｜a｜｜b｜cs θ.
a·b＝⑨ x1x2＋y1y2 .
模
｜a｜＝a·a.
｜a｜＝⑩ x12＋y12 .
夹角
cs θ＝⑪ a·b｜a||b｜ .
cs θ＝x1x2＋y1y2x12＋y12·x22＋y22.
a⊥b的充要条件
a·b＝0.
⑫ x1x2＋y1y2＝0 .
a∥b的充要条件
a＝λb（λ∈R）.
⑬ x1y2－x2y1＝0 .
｜a·b｜与
｜a｜｜b｜的关系
｜a·b｜≤｜a｜｜b｜（当且仅当a∥b时等号成立）.
｜x1x2＋y1y2｜≤
（x12＋y12)(x22＋y22）.
公式法
利用如下公式转化求解.
①a2＝a·a＝｜a｜2或｜a｜＝a·a；
②｜a±b｜＝（a±b）2＝a2±2a·b＋b2；
③若a＝（x，y），则｜a｜＝x2＋y2.
几何法
利用向量的几何意义，即利用向量加、减法的平行四边形法则或三角形法则作出向量，再利用余弦定理等求解.
定义法
当a，b是非坐标形式时，由cs θ＝a·b｜a||b｜求解.
坐标法
若a＝（x1，y1），b＝（x2，y2），则cs＜a，b＞＝x1x2＋y1y2x12＋y12·x22＋y22，＜a，b＞∈[0，π].
解三角
形法
可以把所求两向量的夹角放到三角形中进行求解.注意向量夹角与三角形内角的关系.