

所属成套资源:2025年高考数学精品教案多份
2025年高考数学精品教案第二章 函数 第3讲 函数的奇偶性、周期性与对称性
展开
这是一份2025年高考数学精品教案第二章 函数 第3讲 函数的奇偶性、周期性与对称性,共24页。
学生用书P024
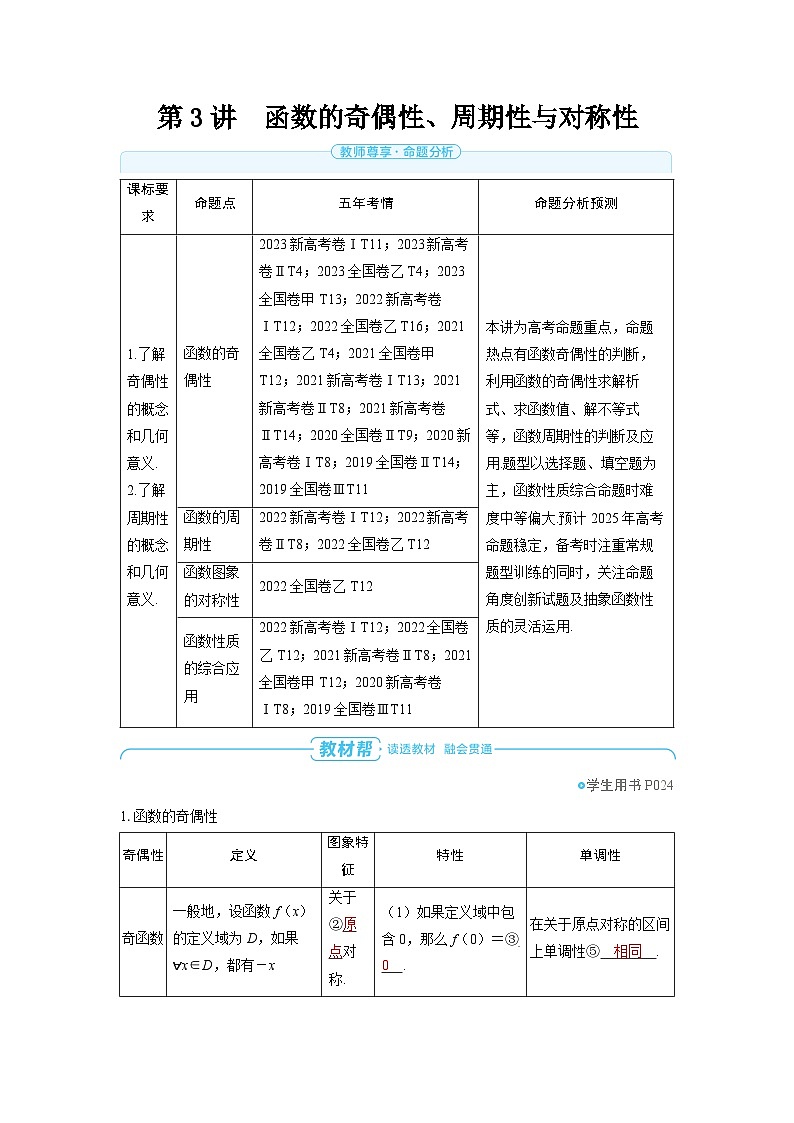
1.函数的奇偶性
注意 (1)只有函数在x=0处有定义时,f(0)=0才是f(x)为奇函数的必要不充分条件;
(2)既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集.
规律总结
1.常见的奇(偶)函数
(1)函数f(x)=ax+a-x为偶函数,函数g(x)=ax-a-x为奇函数;
(2)函数f(x)=ax-a-xax+a-x=a2x-1a2x+1为奇函数,函数g(x)=lgab-xb+x为奇函数;
(3)函数f(x)=lga(x+x2+1)为奇函数,函数g(x)=lga(x2+1-x)也为奇函数.
2.函数奇偶性的拓展结论
(1)若函数y=f(x+a)是偶函数,则f(x+a)=f(-x+a),函数y=f(x)的图象关于直线x=a对称.
(2)若函数y=f(x+b)是奇函数,则f(x+b)+f(-x+b)=0,函数y=f(x)的图象关于点(b,0)中心对称.
2.函数的周期性
(1)周期函数
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且⑨ f(x+T)=f(x) ,那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小的正数就叫做
f(x)的⑩ 最小 正周期.
注意 并不是所有的周期函数都有最小正周期,如f(x)=5.
常用结论
函数周期性的常用结论
设函数y=f(x),x∈R,a>0,a≠b.
(1)若f(x+a)=-f(x),则2a是函数f(x)的周期;
(2)若f(x+a)=±1f(x),则2a是函数f(x)的周期;
(3)若f(x+a)=f(x+b),则|a-b|是函数f(x)的周期.
3.函数图象的对称性
已知函数f(x)是定义在R上的函数,
(1)若f(a+x)=f(b-x) 恒成立,则y=f(x) 的图象关于直线⑪ x=a+b2 对称.
(2)若f(a+x)+f(b-x)=c,则y=f(x)的图象关于点⑫ (a+b2,c2) 对称.
注意 (1)奇、偶函数的图象平移之后对应的函数不一定有奇偶性,但其图象一定有对称性.(2)注意区分抽象函数的周期性与对称性的表示,周期性的表示中,括号内x的符号相同,对称性的表示中,括号内x的符号相反.
常用结论
函数f(x)图象的对称性与周期的关系
(1)若函数f(x)的图象关于直线x=a与直线x=b对称,则函数f(x)的周期为2|b-a|;
(2)若函数f(x)的图象既关于点(a,0)对称,又关于点(b,0)对称,则函数f(x)的周期为2|b-a|;
(3)若函数f(x)的图象既关于直线x=a对称,又关于点(b,0)对称,则函数f(x)的周期为4|b-a|.
1.已知函数f(x)为奇函数,当x>0时,f(x)=x2+1x,则f(-1)=( A )
A.-2B.0C.1D.2
2.函数f(x)=x+1x图象的对称中心为( B )
A.(0,0)B.(0,1)C.(1,0)D.(1,1)
解析 由题知f(x)=x+1x=1+1x,其图象可由y=1x的图象向上平移一个单位长度得到,又y=1x的图象关于(0,0)对称,所以f(x)=1+1x的图象关于(0,1)对称.
3.[多选]以下函数为偶函数的是( AC )
A.f(x)=x2-1B.f(x)=x3
C.f(x)=x2+cs xD.f(x)=1x+|x|
4.已知函数f(x)为R上的偶函数,且当x<0时,f(x)=x(x-1),则当x>0时,
f(x)= x(x+1) .
5.已知定义在R上的函数f(x)满足f(x)=f(x-2),当x∈[0,2)时,f(x)=x2-4x,则当x∈[4,6)时,f(x)= x2-12x+32 .
解析 设x∈[4,6),则x-4∈[0,2),则f(x-4)=(x-4)2-4(x-4)=x2-12x+32.又f(x)=f(x-2),所以函数f(x)的周期为2,所以f(x-4)=f(x),所以当x∈[4,6)时,f(x)=x2-12x+32.
6.[2024北京市海淀区中国农业大学附属中学模拟]若f(x)=x+a,x0是奇函数,则a= 1 ,b= 1 .
解析 由f(x)为奇函数,知f(-x)=-f(x),当x>0时,可得-x+a=-bx+1,所以b=1,a=1.
学生用书P026
命题点1 函数的奇偶性
角度1 判断函数的奇偶性
例1 (1)[全国卷Ⅰ]设函数f(x),g(x)的定义域都为R,且 f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( B )
A. f(x)g(x)是偶函数B. f(x)|g(x)|是奇函数
C.|f(x)|g(x)是奇函数D.|f(x)g(x)|是奇函数
解析 因为f(x)为奇函数,g(x)为偶函数,所以f(x)g(x)为奇函数,f(x)·
|g(x)|为奇函数,|f(x)|g(x)为偶函数,|f(x)g(x)|为偶函数,故选B.
(2)[2021全国卷乙]设函数f(x)=1-x1+x,则下列函数中为奇函数的是( B )
A.f(x-1)-1B.f(x-1)+1
C.f(x+1)-1D.f(x+1)+1
解析 解法一 因为f(x)=1-x1+x,所以f(x-1)=1-(x-1)1+(x-1)=2-xx,f(x+1)=1-(x+1)1+(x+1)=-xx+2.
对于A,F(x)=f(x-1)-1=2-xx-1=2-2xx,定义域关于原点对称,但不满足F(x)=-F(-x);
对于B,G(x)=f(x-1)+1=2-xx+1=2x,定义域关于原点对称,且满足G(x)=
-G(-x);
对于C,f(x+1)-1=-xx+2-1,定义域不关于原点对称;
对于D,f(x+1)+1=-xx+2+1,定义域不关于原点对称.
故选B.
解法二 f(x)=1-x1+x=2-(x+1)1+x=21+x-1,为保证函数变换之后为奇函数,需将函数y=
f(x)的图象向右平移一个单位长度,再向上平移一个单位长度,得到的图象对应的函数为y=f(x-1)+1,故选B.
方法技巧
1.(1)函数定义域关于原点对称是函数有奇偶性的前提条件;(2)若定义域关于原点对称,则判断f(x)与f(-x)是否具有等量关系,具体运算中,可转化为判断f(x)+
f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数)是否成立.
2.在公共定义域内有:奇函数±奇函数=奇函数,偶函数±偶函数=偶函数,奇函数×奇函数=偶函数,偶函数×偶函数=偶函数,奇函数×偶函数=奇函数.
注意 对于分段函数奇偶性的判断,要分段判断f(-x)=f(x)或f(-x)=-f(x)是否成立,只有当所有区间都满足相同关系时,才能判断该分段函数的奇偶性.
角度2 函数奇偶性的应用
例2 (1)[2023新高考卷Ⅱ]若f(x)=(x+a)·ln2x-12x+1为偶函数,则a=( B )
A.-1B.0C.12D.1
解析 解法一 设g(x)=ln 2x-12x+1,易知g(x)的定义域为(-∞,-12)∪(12,
+∞),且g(-x)=ln -2x-1-2x+1=ln 2x+12x-1=-ln 2x-12x+1=-g(x),所以g(x)为奇函数.若
f(x)=(x+a)ln 2x-12x+1为偶函数,则y=x+a应为奇函数,所以a=0,故选B.
解法二 因为f(x)=(x+a)ln 2x-12x+1为偶函数,f(-1)=(a-1)ln 3,f(1)=(a+1)ln 13=-(a+1)ln 3,所以(a-1)ln 3=-(a+1)ln 3,解得a=0,经检验,满足题意,故选B.
(2)[2024江苏南通模拟]已知定义在R上的函数f(x),g(x)分别是奇函数和偶函数,且f(x)+g(x)=x2-2x,则f(2)+g(1)= -3 .
解析 由f(x)是奇函数,g(x)是偶函数,得f(-x)=-f(x),g(-x)=g(x),∵f(x)+g(x)=x2-2x,∴f(-x)+g(-x)=(-x)2-2(-x)=x2+2x,即
-f(x)+g(x)=x2+2x,则有f(x)=-2x,g(x)=x2,则f(2)+g(1)=-4+1=-3.
方法技巧
函数奇偶性的应用类型及解题策略
(1)求函数解析式或函数值:借助奇偶性转化为求已知区间上的函数解析式或函数值,或利用奇偶性构造关于f(x)的方程(组)求解析式.
(2)求参数值:利用定义域关于原点对称或f(x)±f(-x)=0列方程(组)求解,对于在x=0处有定义的奇函数f(x),可考虑列等式f(0)=0求解.
注意 利用特殊值法求参数时要检验.
训练1 (1)[2024辽宁鞍山一中模拟]下列函数中,既是偶函数又在(0,+∞)上单调递增的是( C )
A.f(x)=xln x
B.f(x)=ln(-x+x2+1)
C.f(x)=ex+e-x
D.f(x)=ex-e-x
解析 对于A,因为f(x)=xln x的定义域为(0,+∞),不关于原点对称,所以f(x)=xln x不是偶函数,故A选项不符合题意;对于B,因为f(x)=ln(-x+x2+1)的定义域为R,关于原点对称,f(x)+f(-x)=ln(-x+x2+1)+ln(x+x2+1)=ln 1=0,所以f(x)=ln(-x+x2+1)是奇函数,故B选项不符合题意;对于C,因为f(x)=ex+e-x的定义域为R,关于原点对称,且f(-x)=e-x+ex=f(x),所以
f(x)=ex+e-x是偶函数.f '(x)=ex-e-x,当x∈(0,+∞)时,有ex>e0=1>e-x,则f '(x)=ex-e-x>0,所以f(x)=ex+e-x在(0,+∞)上单调递增,故C选项符合题意;对于D,因为f(x)=ex-e-x的定义域为R,关于原点对称,但f(-x)=e-x-ex=-(ex-e-x)=-f(x),所以f(x)=ex-e-x是奇函数,故D选项不符合题意.故选C.
(2)[2024江苏省扬州中学模拟]定义在R上的奇函数f(x),当x≥0时,f(x)=2x-a·3-x,当x<0时, f(x)= 3x-2-x .
解析 因为函数f(x)为奇函数,定义域为R,所以f(0)=20-a×30=0,解得a=1.若x<0,则-x>0,所以f(-x)=2-x-3x,又f(x)为奇函数,所以当x<0时,f(x)=-f(-x)=3x-2-x,即当x<0时,f(x)=3x-2-x.
命题点2 函数的周期性
例3 (1)已知f(x+1)是定义在R上且周期为2的函数,当x∈[-1,1)时,f(x)=-2x2+4,-1≤x
相关教案
这是一份2025年高考数学精品教案第二章 函数 第1讲 函数的概念及其表示,共12页。
这是一份2025年高考数学精品教案第二章 函数 第2讲 函数的单调性与最值,共17页。
这是一份高考数学一轮复习教案 第2章_第3节_函数的奇偶性与周期性(含答案解析),共14页。








