

所属成套资源:2025年高考数学精品教案多份
2025年高考数学精品教案第二章 函数 第2讲 函数的单调性与最值
展开
这是一份2025年高考数学精品教案第二章 函数 第2讲 函数的单调性与最值,共17页。
学生用书P020
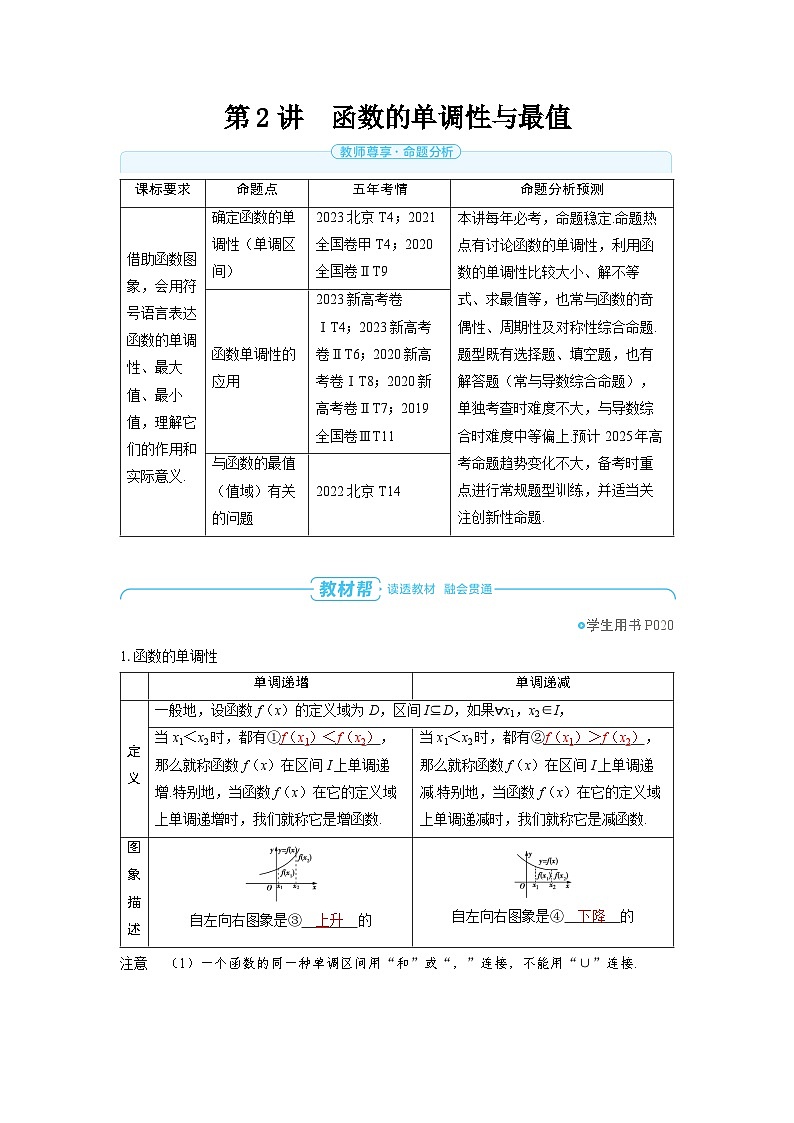
1.函数的单调性
注意 (1)一个函数的同一种单调区间用“和”或“,”连接,不能用“∪”连接.
(2)“函数f(x)的单调区间为M ”与“函数f(x)在区间N 上单调”是两个不同的概念,显然N⊆M .
(3)注意“增(减)函数”与“单调递增(减)”的区别,只有在定义域上单调递增(减),才能称它是增(减)函数.
规律总结
1.函数单调性的两个等价变形
若∀x1,x2∈D(x1≠x2),则
(1)f(x1)-f(x2)x1-x2>0(或(x1-x2)[f(x1)-f(x2)]>0)⇔f(x)在区间D上单调递增;
(2)f(x1)-f(x2)x1-x2<0(或(x1-x2)[f(x1)-f(x2)]<0)⇔f(x)在区间D上单调递减.
2.函数单调性的常用结论
(1)在公共定义域内,增函数+增函数=增函数,减函数+减函数=减函数;
(2)当f(x)≠0时,函数f(x)与-f(x),1f(x)在公共定义域内单调性相反;
(3)复合函数y=f(g(x))的单调性与y=f(t),t=g(x)的单调性有关,即“同增异减”.
3.对勾函数y=ax+bx(a>0,b>0)的单调性与最值
如图,
(1)单调性:增区间为(-∞,-ba),(ba,+∞);减区间(-ba,0),(0,ba).
(2)最值:当x>0时,函数y=ax+bx在x=ba处取得最小值2ab;当x<0时,函数y=ax+bx在x=-ba处取得最大值-2ab.
注意 对勾函数y=ax+bx(a>0,b>0)的图象有两条渐近线:x=0,y=ax.
2.函数的最值
注意 闭区间上的连续函数一定存在最大值和最小值,当函数在闭区间上单调时最值一定在端点处取得.
1.以下说法正确的是( D )
A.对于函数y=f(x),若f(1)<f(3),则f(x)为增函数
B.函数y=1x的单调递减区间为(-∞,0)∪(0,+∞)
C.若函数y=f(x)在[1,+∞)上单调递增,则函数的单调递增区间是[1,+∞)
D.闭区间上的单调函数,其最值一定在区间端点处取到
2.[教材改编]函数y=|x|-1的单调递减区间为( B )
A.(0,+∞)B.(-∞,0)
C.(-∞,-1)D.(-1,+∞)
3.[教材改编]y=2x+1x-3的值域为 (-∞,2)∪(2,+∞) .
解析 y=2x+1x-3=2(x-3)+7x-3=2+7x-3,显然7x-3≠0,所以y≠2.故函数的值域为(-∞,2)∪(2,+∞).
4.y=2x-x-1的值域为 [158,+∞) .
解析 设t=x-1,则x=t2+1,且t≥0,所以y=2(t2+1)-t=2(t-14)2+158,由t≥0,可得函数的值域为[158,+∞).
学生用书P022
命题点1 确定函数的单调性(单调区间)
例1 (1)[2023北京高考]下列函数中,在区间(0,+∞)上单调递增的是( C )
A.f(x)=-ln xB.f(x)=12x
C.f(x)=-1xD.f(x)=3|x-1|
解析 对于A,因为函数y=ln x在(0,+∞)上单调递增,所以f(x)=-ln x在(0,+∞)上单调递减,所以A不符合要求;对于B,因为f(x)=12x=(12)x在(0,+∞)上单调递减,所以B不符合要求;对于C,由反比例函数的图象可知,f(x)=-1x在(0,+∞)上单调递增,所以C符合要求;对于D,当0<x<1时,y=3|x-1|=31-x在(0,1)上单调递减,所以D不符合要求.故选C.
(2)[全国卷Ⅱ]函数f(x)=ln(x2-2x-8)的单调递增区间是( D )
A.(-∞,-2)B.(-∞,1)
C.(1,+∞)D.(4,+∞)
解析 由x2-2x-8>0,得x<-2或x>4.因此,函数f(x)=ln(x2-2x-8)的定义域是(-∞,-2)∪(4,+∞).(先求函数f(x)的定义域)
易知函数y=x2-2x-8在(-∞,-2)上单调递减,在(4,+∞)上单调递增,函数
y=ln t为(0,+∞)上的增函数,由复合函数的单调性知,f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞).故选D.
(3)讨论函数f(x)=axx-1(a≠0)在(-1,1)上的单调性.
解析 解法一(导数法) f '(x)=a(x-1)-ax(x-1)2=-a(x-1)2.
当a>0时,f '(x)<0,函数f(x)在(-1,1)上单调递减;
当a<0时,f '(x)>0,函数f(x)在(-1,1)上单调递增.
解法二(定义法) 设-1<x1<x2<1,f(x)=a(x-1+1x-1)=a(1+1x-1),则f(x1)-
f(x2)=a(1+1x1-1)-a(1+1x2-1)=a(x2-x1)(x1-1)(x2-1).
由于-1<x1<x2<1,
所以x2-x1>0,x1-1<0,x2-1<0,
故当a>0时,f(x1)-f(x2)>0,即f(x1)>f(x2),函数f(x)在(-1,1)上单调递减;
当a<0时,f(x1)-f(x2)<0,即f(x1)<f(x2),函数f(x)在(-1,1)上单调递增.
方法技巧
判断函数的单调性的方法
(1)定义法;(2)图象法;(3)导数法;(4)性质法.
训练1 (1)函数g(x)=x·|x-1|+1的单调递减区间为( B )
A.(-∞,12]B.[12,1]
C.[1,+∞)D.(-∞,12)∪[1,+∞)
解析 g(x)=x·|x-1|+1=x2-x+1,x≥1,-x2+x+1,x
相关教案
这是一份新高考数学一轮复习讲练教案3.2 第1课时 导数与函数的单调性、极值与最值(含解析),共6页。
这是一份新高考数学一轮复习讲练教案2.2 第1课时 函数的单调性与最值、奇偶性、周期性(含解析),共7页。
这是一份高考数学一轮复习教案 第2章_第2节_函数的单调性与最值(含答案解析),共12页。









