湖南省部分省示范性高中2024-2025学年高二上学期开学考试数学试题（Word版附解析）

这是一份湖南省部分省示范性高中2024-2025学年高二上学期开学考试数学试题（Word版附解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

时量：120分钟 满分：150分
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
1. 复数的虚部为（ ）
A. B. C. D.
2 已知集合，则（ ）
A. B.
C D.
3. 已知，则（ ）
A. B. C. D.
4. 已知命题甲：“实数x，y满足”，乙“实数x，y满足”，则甲是乙的（ ）
A 必要不充分条件B. 充分不必要条件
C. 充要条件D. 既不充分也不必要条件
5 已知，则（ ）
A. B. C. D.
6. 将函数的图象所有点的横坐标变为原来的2倍，纵坐标不变，得到函数的图象，若在区间上单调递减，则的最大值为（ ）
A. B. C. D. 1
7. 由于猪肉的价格有升也有降，小张想到两种买肉方案.第一种方案：每次买3斤猪肉；第二种方案：每次买50元猪肉.下列说法正确的是（ ）
A. 采用第一种方案划算B. 采用第二种方案划算
C. 两种方案一样D. 采用哪种方案无法确定
8. 表示不超过实数x的最大整数，已知奇函数的定义域为R，为偶函数，，对于区间上的任意都有，若关于x的不等式对任意的恒成立，则的最大值是（ ）
A. 0B. 1C. 2D. 3
二、选择题：本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9. 设向量，则下列说法错误的是（ ）
A. 若与的夹角为钝角，则
B. 的最小值为9
C. 与共线的单位向量只有一个，为
D. 若，则
10. 随机抽取8位同学对2024年数学新高考Ⅰ卷的平均分进行预估，得到一组样本数据如下：97，98，99，100，101，103，104，106，则下列关于该样本的说法正确的有（ ）
A. 均值为101B. 极差为9
C. 方差为8D. 第60百分位数为101
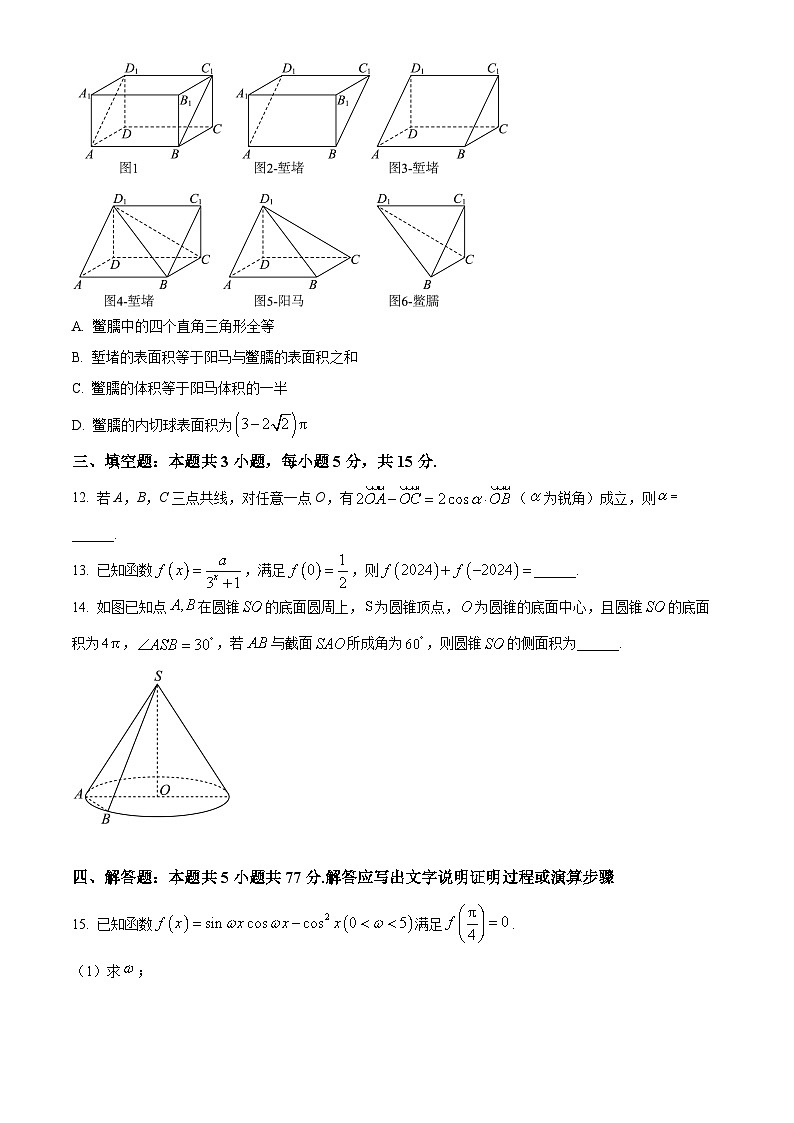
11. 阳马和鳖臑[biēnà]是我国古代对一些特殊锥体的称谓，取一长方体按下图斜割一分为二，得两个一模一样的三棱柱（图2，图3），称为堑堵.再沿堑堵的一顶点与相对的棱剖开（图4），得四棱锥和三棱锥各一个.以矩形为底，有一棱与底面垂直的四棱锥，称为阳马（图5）.余下的三棱锥是由四个直角三角形组成的四面体，称为鳖臑（图6）.若图1中的长方体是棱长为1的正方体，则下列结论正确的是（ ）
A. 鳖臑中的四个直角三角形全等
B. 堑堵的表面积等于阳马与鳖臑的表面积之和
C. 鳖臑的体积等于阳马体积的一半
D. 鳖臑的内切球表面积为
三、填空题：本题共3小题，每小题5分，共15分.
12. 若A，B，C三点共线，对任意一点O，有（为锐角）成立，则______.
13. 已知函数，满足，则______.
14. 如图已知点在圆锥的底面圆周上，为圆锥顶点，为圆锥的底面中心，且圆锥的底面积为，，若与截面所成角为，则圆锥的侧面积为______.
四、解答题：本题共5小题共77分.解答应写出文字说明证明过程或演算步骤
15. 已知函数满足.
（1）求；
（2）求在区间上的最小值.
16. 的内角A，B，C的对边分别为a，b，c已知.
（1）求A；
（2）若，求的面积.
17. 随着时代不断地进步，人们的生活条件也越来越好，越来越多的人注重自己的身材，其中体脂率是一个很重要的衡量标准根据一般的成人体准，女性体脂率的正常范围是至，男性的正常范围是至.这一范围适用于大多数成年人，可以帮助判断个体是否存在肥胖的风险.某市有关部门对全市万名成年女性的体脂率进行一次抽样调查统计，抽取了名成年女性的体脂率作为样本绘制频率分布直方图如图.

（1）求a；
（2）如果女性体脂率为至属“偏胖”，体脂率超过属“过胖”，那么全市女性“偏胖”，“过胖”各约有多少人？
（3）小王说：“我的体脂率是调查所得数据的中位数.”小张说：“我的体脂率是调查所得数据的平均数.”那么谁的体脂率更低？
18. 如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．
（1）证明：l⊥平面PDC；
（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．
19. 在扔硬币猜正反游戏中，当硬币出现正面时，猜是正面的概率为.猜是反面的概率为；当硬币出现反面时，猜是反面的概率为，猜是正面的概率为.假设每次扔硬币相互独立.
（1）若两次扔硬币分别为“正反”，设猜测全部正确与猜测全部错误的概率分别为，试比较的大小；
（2）若不管扔硬币是正面还是反面猜对的概率都大于猜错的概率，
（i）从下面①②③④中选出一定错误的结论：
①；②；③，④
（ii）从（i）中选出一个可能正确结论作为条件.用表示猜测的正反文字串，将中正面的个数记为，如“正反正反”，则，若扔四次硬币分别为“正正反反”，求的取值范围.（暨入学检测）
数学
时量：120分钟 满分：150分
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
1. 复数的虚部为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】利用复数除法法则计算出，得到虚部.
【详解】，
故虚部为.
故选：A
2. 已知集合，则（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】先解不等式得到A=x−1−1，由补集和并集运算法则，结合子集的概念得到答案.
【详解】A选项，A=x−115=xx>−1，
故，则不是的子集，A错误；
B选项，或，故不是的子集，B错误；
C选项，，C正确；
D选项，，D错误.
故选：C
3. 已知，则（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据余弦二倍角公式可得结果.
【详解】因为，
所以或，又，所以.
故选：A.
4. 已知命题甲：“实数x，y满足”，乙“实数x，y满足”，则甲是乙的（ ）
A. 必要不充分条件B. 充分不必要条件
C. 充要条件D. 既不充分也不必要条件
【答案】B
【解析】
【分析】，充分性成立，举出反例得到必要性不成立，得到答案.
【详解】，充分性成立，
但不能得到，比如当时，满足，但不满足，必要性不成立，
故甲是乙的充分不必要条件.
故选：B
5. 已知，则（ ）
A. B. C. D.
【答案】C
【解析】
【分析】结合指数函数，对数函数的性质估计的范围，由此比较它们的大小.
【详解】函数在上为增函数，又，
所以，即，
函数在上为减函数，又，
所以，即，
函数在上为减函数，，
所以，即，
所以.
故选：C.
6. 将函数的图象所有点的横坐标变为原来的2倍，纵坐标不变，得到函数的图象，若在区间上单调递减，则的最大值为（ ）
A. B. C. D. 1
【答案】D
【解析】
【分析】先根据伸缩变换得到，求出，结合函数单调性得到不等式，求出，得到答案.
【详解】，
，，
要想在区间上单调递减，则，
解得，故的最大值为1.
故选：D
7. 由于猪肉的价格有升也有降，小张想到两种买肉方案.第一种方案：每次买3斤猪肉；第二种方案：每次买50元猪肉.下列说法正确的是（ ）
A. 采用第一种方案划算B. 采用第二种方案划算
C. 两种方案一样D. 采用哪种方案无法确定
【答案】B
【解析】
【分析】设两次购买猪肉的价格分别为，，表达出两种方案购买的均价，结合基本不等式比较出大小，得到答案.
【详解】不妨设两次购买猪肉的价格分别为，，
第一种方案，均价为，
第二种方案，均价为，
其中，当且仅当时，等号成立，
，当且仅当时，等号成立，
故，当且仅当时，等号成立，
所以采用第二种方案划算.
故选：B
8. 表示不超过实数x的最大整数，已知奇函数的定义域为R，为偶函数，，对于区间上的任意都有，若关于x的不等式对任意的恒成立，则的最大值是（ ）
A. 0B. 1C. 2D. 3
【答案】C
【解析】
【分析】根据函数的对称性，奇偶性得到的一个周期为8，由fx1+4−fx2+4x2−x1>0变形得到在0,2上单调递减，故在上单调递减，由函数周期，奇偶性，对称性得到在R上的最小值为，故，解得，求出的最大值为2.
【详解】为偶函数，故关于对称，，
又为奇函数，故f−x=−fx，即，
所以，
所以，故，
的一个周期为8，
区间0,2上的任意都有fx1+4−fx2+4x2−x1>0⇒fx1+4−fx2+4x1+4−x2+4<0，
令，则在0,2上单调递减，
故在上单调递减，
因为为奇函数，所以在上单调递减，
又的一个周期为8，故在2,4上单调递减，
又关于对称，故，
故在上单调递减，
由对称性可知在上单调递增，
且的一个周期为8，
故在R上的最小值为，
不等式对任意的x∈R恒成立，
故，解得，
当时，，当时，，
当时，，
故的最大值为2
故选：C
【点睛】结论点睛：设函数y=fx，，，．
（1）若，则函数的周期为2a；
（2）若，则函数的周期为2a；
（3）若，则函数的周期为2a；
（4）若，则函数的周期为2a；
（5）若，则函数的周期为；
（6）若函数的图象关于直线与对称，则函数的周期为；
（7）若函数的图象既关于点对称，又关于点对称，则函数的周期为；
（8）若函数的图象既关于直线对称，又关于点对称，则函数的周期为；
（9）若函数是偶函数，且其图象关于直线对称，则的周期为2a；
（10）若函数是奇函数，且其图象关于直线对称，则的周期为4a．
二、选择题：本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9. 设向量，则下列说法错误的是（ ）
A. 若与的夹角为钝角，则
B. 的最小值为9
C. 与共线的单位向量只有一个，为
D. 若，则
【答案】BC
【解析】
【分析】A选项，且不反向共线，得到不等式，求出；B选项，利用模长公式得到的最小值为3；C选项，求出，从而得到利用求出答案；D选项，利用模长公式得到方程，求出.
【详解】A选项，与的夹角为钝角，故且不反向共线，
则且，解得且，
综上，，A正确；
B选项，，当且仅当时，等号成立，故的最小值为3，B错误；
C选项，，与共线的单位向量有2个，
为，C错误；
D选项，若，则，解得，D正确.
故选：BC
10. 随机抽取8位同学对2024年数学新高考Ⅰ卷的平均分进行预估，得到一组样本数据如下：97，98，99，100，101，103，104，106，则下列关于该样本的说法正确的有（ ）
A. 均值为101B. 极差为9
C. 方差为8D. 第60百分位数为101
【答案】ABD
【解析】
【分析】A选项，利用均值定义进行求解；B选项，利用极差定义进行求解；C选项，在A选项基础上，利用方差公式进行求解；D选项，，故从小到大，选择第5个数作为第60百分位数，得到答案.
【详解】A选项，均值为，A正确；
B选项，极差为，B正确；
C选项，方差为，C错误；
D选项，因为，故从小到大，选择第5个数作为第60百分位数，即101，D正确.
故选：ABD
11. 阳马和鳖臑[biēnà]是我国古代对一些特殊锥体的称谓，取一长方体按下图斜割一分为二，得两个一模一样的三棱柱（图2，图3），称为堑堵.再沿堑堵的一顶点与相对的棱剖开（图4），得四棱锥和三棱锥各一个.以矩形为底，有一棱与底面垂直的四棱锥，称为阳马（图5）.余下的三棱锥是由四个直角三角形组成的四面体，称为鳖臑（图6）.若图1中的长方体是棱长为1的正方体，则下列结论正确的是（ ）
A. 鳖臑中的四个直角三角形全等
B. 堑堵的表面积等于阳马与鳖臑的表面积之和
C. 鳖臑的体积等于阳马体积的一半
D. 鳖臑的内切球表面积为
【答案】CD
【解析】
【分析】由条件，求鳖臑的各棱长，判断A，结合多面体表面积定义及堑堵、鳖臑、阳马的结构特征求出它们的表面积，判断B，根据锥体体积公式求鳖臑和阳马的体积判断C，利用鳖臑的体积和表面积可求其内切球的半径，结合球的表面积公式求球的表面积判断D.
【详解】由已知，，
所以，，
所以和不全等，A错误；
堑堵的表面积，
由已知，，
所以，
阳马的表面积，
鳖臑的表面积，，
所以堑堵的表面积不等于阳马与鳖臑的表面积之和，B错误，
鳖臑的体积，
阳马的体积，
所以鳖臑的体积等于阳马体积的一半，C正确；
设鳖臑的内切球的半径为，
因为鳖臑表面积，鳖臑的体积，又，
所以，
所以鳖臑的内切球表面积为，D正确.
故选：CD.
三、填空题：本题共3小题，每小题5分，共15分.
12. 若A，B，C三点共线，对任意一点O，有（为锐角）成立，则______.
【答案】
【解析】
【分析】根据三点共线得到存在使得，故，结合，得到，从而求出.
【详解】因为A，B，C三点共线，所以存在使得，
即，
故，将其代入得，
，
即，
由于上式恒成立，，故，解得，
因为为锐角，所以.
故答案为：
13. 已知函数，满足，则______.
【答案】1
【解析】
【分析】利用，求出，代入求值.
【详解】，故，解得，
则，.
故答案：1
14. 如图已知点在圆锥的底面圆周上，为圆锥顶点，为圆锥的底面中心，且圆锥的底面积为，，若与截面所成角为，则圆锥的侧面积为______.
【答案】
【解析】
【分析】设圆锥的底面半径为，母线长为，由底面面积为可求，证明为直线与截面所成的角，解三角形求，由此可求圆锥的侧面积.
【详解】设圆锥的底面半径为，母线长为，
因为圆锥的底面积为，
所以，故，
过点作，垂足为，连接，
由已知平面，平面，
所以，，平面，
所以平面，所以在平面上的射影为AD，
所以为直线与截面所成的角，
由已知，又，
所以为等边三角形，故，
因为，，
由余弦定理可得，
所以，
所以，
所以圆锥的侧面积为.
故答案为：.
四、解答题：本题共5小题共77分.解答应写出文字说明证明过程或演算步骤
15. 已知函数满足.
（1）求；
（2）求在区间上的最小值.
【答案】（1）1 （2）
【解析】
【分析】（1）化简后代入，求出；
（2）化简得到，由求出，利用整体法求出函数的最小值.
【小问1详解】
，
故，即，
因为，所以，故，解得，
【小问2详解】
，
，，故，
则，
故在区间的最小值为.
16. 的内角A，B，C的对边分别为a，b，c已知.
（1）求A；
（2）若，求的面积.
【答案】（1）
（2）
【解析】
【分析】（1）化简，结合正弦和角公式，诱导公式得到，由正弦定理得到，求出A；
（2）利用余弦定理得到，利用三角形面积公式求出答案.
【小问1详解】
，
故，
即，
由于，
故，
由正弦定理得，
因为，所以，故，
即，
因为，所以；
【小问2详解】
由余弦定理得，
又，，故，解得，
则.
17. 随着时代不断地进步，人们的生活条件也越来越好，越来越多的人注重自己的身材，其中体脂率是一个很重要的衡量标准根据一般的成人体准，女性体脂率的正常范围是至，男性的正常范围是至.这一范围适用于大多数成年人，可以帮助判断个体是否存在肥胖的风险.某市有关部门对全市万名成年女性的体脂率进行一次抽样调查统计，抽取了名成年女性的体脂率作为样本绘制频率分布直方图如图.

（1）求a；
（2）如果女性体脂率为至属“偏胖”，体脂率超过属“过胖”，那么全市女性“偏胖”，“过胖”各约有多少人？
（3）小王说：“我的体脂率是调查所得数据的中位数.”小张说：“我的体脂率是调查所得数据的平均数.”那么谁的体脂率更低？
【答案】（1）；
（2）全市女性“偏胖”的人数约为，“过胖”的人数约为；
（3）小张的体脂率更低.
【解析】
【分析】（1）由所有矩形条的面积和为，列方程可求；
（2）求出样本中女性“偏胖”，“过胖”的频率，由此估计全市女性“偏胖”，“过胖”的人数；
（3）求样本的中位数，平均数可得小王和小张的体脂率，由此可得结论.
【小问1详解】
由频率直方图可得，，
所以.
【小问2详解】
由频率分布直方图可得样本中女性“偏胖”的频率为，
样本中女性“过胖”的频率为，
所以全市女性“偏胖”的人数约为，
全市女性 “过胖”的人数约为，
【小问3详解】
调查所得数据的平均数为，
设调查所得数据的中位数为，
因为，，
所以，
所以，
所以，
所以调查所得数据的中位数约为，
所以小王的体脂率约为，小张的体脂率为，
所以小张的体脂率更低.
18. 如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．
（1）证明：l⊥平面PDC；
（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．
【答案】（1）证明见解析；（2）.
【解析】
【分析】（1）利用线面垂直的判定定理证得平面，利用线面平行的判定定理以及性质定理，证得，从而得到平面；
（2）方法一：根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点，之后求得平面的法向量以及向量PB的坐标，求得的最大值，即为直线与平面所成角的正弦值的最大值.
【详解】（1）证明：
在正方形中，，因为平面，平面，
所以平面，又因为平面，平面平面，
所以，因为在四棱锥中，底面是正方形，所以且平面，所以
因，所以平面．
（2）［方法一］【最优解】：通性通法
因为两两垂直，建立空间直角坐标系，如图所示：
因为，设，
设，则有，
设平面的法向量为，
则，即，
令，则，所以平面的一个法向量为，则
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB与平面QCD所成角的正弦值等于，当且仅当时取等号，所以直线与平面所成角的正弦值的最大值为.
［方法二］：定义法
如图2，因平面，，所以平面．
在平面中，设．
在平面中，过P点作，交于F，连接．
因为平面平面，所以．
又由平面，平面，所以平面．又平面，所以．又由平面平面，所以平面，从而即为与平面所成角．
设，在中，易求．
由与相似，得，可得．
所以，当且仅当时等号成立．
［方法三］：等体积法
如图3，延长至G，使得，连接，，则，过G点作平面，交平面于M，连接，则即为所求．
设，在三棱锥中，．
在三棱锥中，．
由得，
解得，
当且仅当时等号成立．
在中，易求，所以直线PB与平面QCD所成角的正弦值的最大值为．
【整体点评】（2）方法一：根据题意建立空间直角坐标系，直线PB与平面QCD所成角的正弦值即为平面的法向量与向量PB的夹角的余弦值的绝对值，即，再根据基本不等式即可求出，是本题的通性通法，也是最优解；
方法二：利用直线与平面所成角定义，作出直线PB与平面QCD所成角，再利用解三角形以及基本不等式即可求出；
方法三：巧妙利用，将线转移，再利用等体积法求得点面距，利用直线PB与平面QCD所成角的正弦值即为点面距与线段长度的比值的方法，即可求出．
19. 在扔硬币猜正反游戏中，当硬币出现正面时，猜是正面的概率为.猜是反面的概率为；当硬币出现反面时，猜是反面的概率为，猜是正面的概率为.假设每次扔硬币相互独立.
（1）若两次扔硬币分别为“正反”，设猜测全部正确与猜测全部错误的概率分别为，试比较的大小；
（2）若不管扔硬币是正面还是反面猜对的概率都大于猜错的概率，
（i）从下面①②③④中选出一定错误的结论：
①；②；③，④
（ii）从（i）中选出一个可能正确的结论作为条件.用表示猜测的正反文字串，将中正面的个数记为，如“正反正反”，则，若扔四次硬币分别为“正正反反”，求的取值范围.
【答案】（1）答案见解析；
（2）答案见解析.
【解析】
【分析】（1）根据独立事件概率乘法公式求，作差可得，
分别在条件下确定差的正负，由此可得的大小关系，
（2）（i）由条件证明，由不等式性质可求的范围，由此确定一定错误的结论；
（ii）由条件，结合互斥事件概率加法公式和独立事件概率乘法公式求，
若选①，令，求出的范围，化简，结合二次函数性质求其范围；
若选③，令，结合对勾函数性质求的范围，化简，结合二次函数性质求其范围；
【小问1详解】
猜测全部正确的概率为，
猜测全部错误的概率为，
因为，
所以当时，，
当时，，
当时，，
【小问2详解】
（i）若不管扔硬币是正面还是反面，猜对的概率都大于猜错的概率，
则α>1−αβ>1−β，解得α>12β>12，
所以，
所以，
因此，②④一定错误，
（ii）若扔四次硬币分别为“正正反反”，事件包含以下三种情况：
两个正都猜对，且两个反都猜对，其概率为；
有且只有一个正猜对，且有且只有一个反猜对，其概率为；
两个正都猜错，且两个反都猜错，其概率为；
所以，
若选择①，
令，则，其中，
所以，
所以，
记，，
由二次函数的性质可知，在区间上单调递增，
所以，
即的取值范围是
若选择③，
此时，又，
所以，所以，
令，则
，，
由对勾函数性质可得函数在上单调递减，在上单调递增，
所以，
因为 ，，，
所以，，
记，，
由二次函数的性质可知，在区间上单调递减，
所以，即
【点睛】关键点点睛：本题第二小问解决的关键在于结合题意准确理解事件，利用基本事件表示，再结合概率运算公式求其概率表达式.