人教版（2024）八年级上册11.1.2 三角形的高、中线与角平分线优秀课件ppt

这是一份人教版（2024）八年级上册11.1.2 三角形的高、中线与角平分线优秀课件ppt，共26页。PPT课件主要包含了cm²，练一练-选择题，练一练-填空题，练一练-解答题，布置作业等内容，欢迎下载使用。
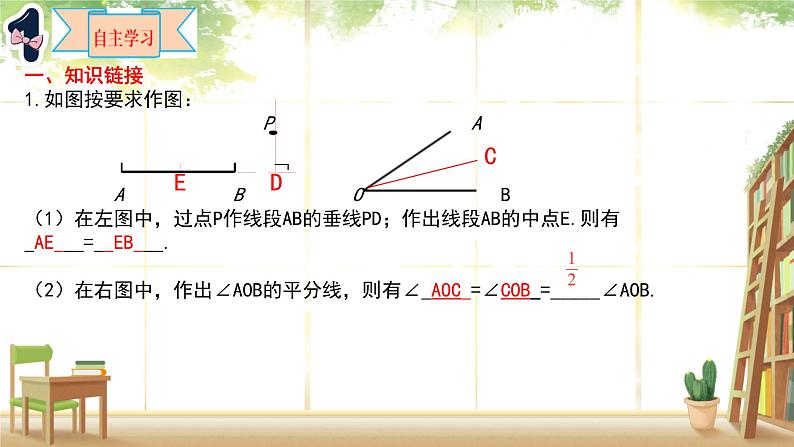
一、知识链接1.如图按要求作图： P A A B O B （1）在左图中，过点P作线段AB的垂线PD；作出线段AB的中点E.则有_AE___=__EB___.（2）在右图中，作出∠AOB的平分线，则有∠_AOC_=∠COB_=_____∠AOB.
1.三角形的高：（1）小学我们已经学过三角形的高，如下图，过点A向它的对边画垂线，作出△ABC的高AD.
（2）自主归纳：①从三角形的一个顶点向它的对边所在直线作垂线，顶点与垂足之间的线段叫做三角形的高线，简称三角形的高.②一个三角形有______条高， 请在左图中作出△ABC的另外两条高.③三角形的高是一条_______.
2.如下图，连接△ABC的顶点A和它的边BC的中点D，类比三角形高线的定义，则所得的线段AD应叫做△ABC的边BC上的_____ 线.并画出△ABC其他的两条中线.
自主归纳：①在三角形中，连接一个顶点与它对边的中点的线段，叫做这个三角形的中线.②一个三角形有_____条中线，每条中线都是一条______.③这三条中线的交点也叫三角形的 。
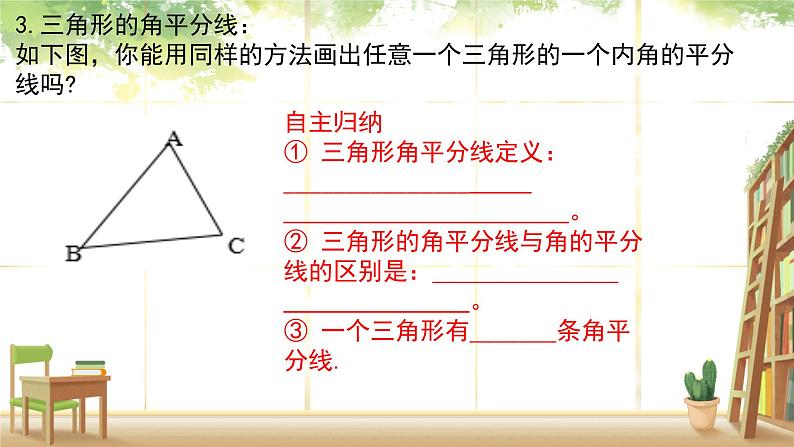
3.三角形的角平分线：如下图，你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
自主归纳① 三角形角平分线定义：_______________ 。② 三角形的角平分线与角的平分线的区别是：_______________ 。③ 一个三角形有_______条角平分线.
4.几何语言表示三角形的高、中线、角平分线
例1：如图所示，在△ABC中，AB＝AC＝5，BC＝6，AD⊥BC于点D，且AD＝4，若点P在边AC上移动，求BP的最小值.
解：由垂线段最短可得，当BP垂直于AC时的值最小因为 AD=4,BC=6所以 = BC AD =12又因为 = AC BP =12 所以 BP =
练习1　在下图中，正确画出△ABC 中边BC 上高的是（ ）．
方法总结：三角形任意一边上的高必须满足：(1)过该边所对的顶点；(2)垂足必须在该边或在该边的延长线上．
解：△ABE，△ABD，△ABC，△AED，△AEC，△ADC.
练习2　如图，写出以AE为高的三角形.
　　画一个锐角三角形、直角三角形、钝角三角形，再分别画出这三个三角形的三条中线.
三角形的三条中线交于一点，这个交点就是三角形的重心.三角形的中线将三角形分成面积相等的两部分
例2　如图所示，AM 是△ABC的中线，△ABM 的面积是 20 平方厘米，求△ABC 的面积.
　　练习3　如图，AD，BE，CF 是△ABC 的三条中线．（1）AC = AE = EC； CD = ； AF = AB；（2）若S△ABC = 12 cm2， 则S△ABD = ．
练习4 在△ABC中，AC＝5cm，AD是△ABC的中线，若△ABD的周长比△ADC的周长大2cm，则BA＝________.
温馨提示：将△ABD与△ADC的周长之差转化为边长的差.
探究3：三角形的角平分线
三角形的一个角的平分线与这个角的对边相交，连接这个角的顶点与交点的线段叫做三角形的角平分线
如图所示AD是 ABC的角平分线
　　画一个锐角三角形、直角三角形、钝角三角形，再分别画出这三个三角形的三条角平分线.
三角形的三条角平分线交于一点，都在三角形内部
例2　如图,在△ABC中,∠BAC=68°，∠B=36°，AD是△ABC的一条角平分线，求∠ADB的度数.
解：∵AD是△ABC的角平分线，∠BAC＝68°， ∴∠DAC＝∠BAD＝34°. 在△ABD中， ∠B+∠ADB+∠BAD＝180°， ∴∠ADB＝180°－∠B－∠BAD ＝180°－36°－34°＝110°.
1.三角形的三条高在（ ）
三角形的内部，外部或边上
如图，AD是△ABC的边BC上的中线，已知AB = 5cm，AC = 3cm.△ABD的面积为a cm2，
（1）S△ABC = ______cm2；
（2）△ABD与△ACD的周长之差为___ cm.
如图，DC平分∠ACB，DE∥BC,∠AED=80°，求∠ECD的度数.