四川省成都市金牛区铁路中学2024-2025学年九年级上学期数学开学考试试卷

这是一份四川省成都市金牛区铁路中学2024-2025学年九年级上学期数学开学考试试卷，共13页。试卷主要包含了分解因式等内容，欢迎下载使用。
1．（4分）下列图形既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
2．（4分）若a＞b，则下列不等式正确的是（ ）
A．﹣4a＞﹣4bB．a＞bC．4﹣a＞4﹣bD．a2＞b2
3．（4分）如图，在△ABC中，∠ABC，∠ACB的平分线交于点O，过点O作EF∥BC分别交AB，AC于点E，F，若AB＝5，AC＝4，则△AEF的周长是（ ）
A．8B．9C．10D．11
4．（4分）下列由左边到右边的变形，属于因式分解的是（ ）
A．B．a2﹣2a﹣1＝（a﹣1）2
C．x2+6x+10＝（x+3）2+1D．m2﹣4m＝m（m﹣4）
5．（4分）下列分式变形正确的是（ ）
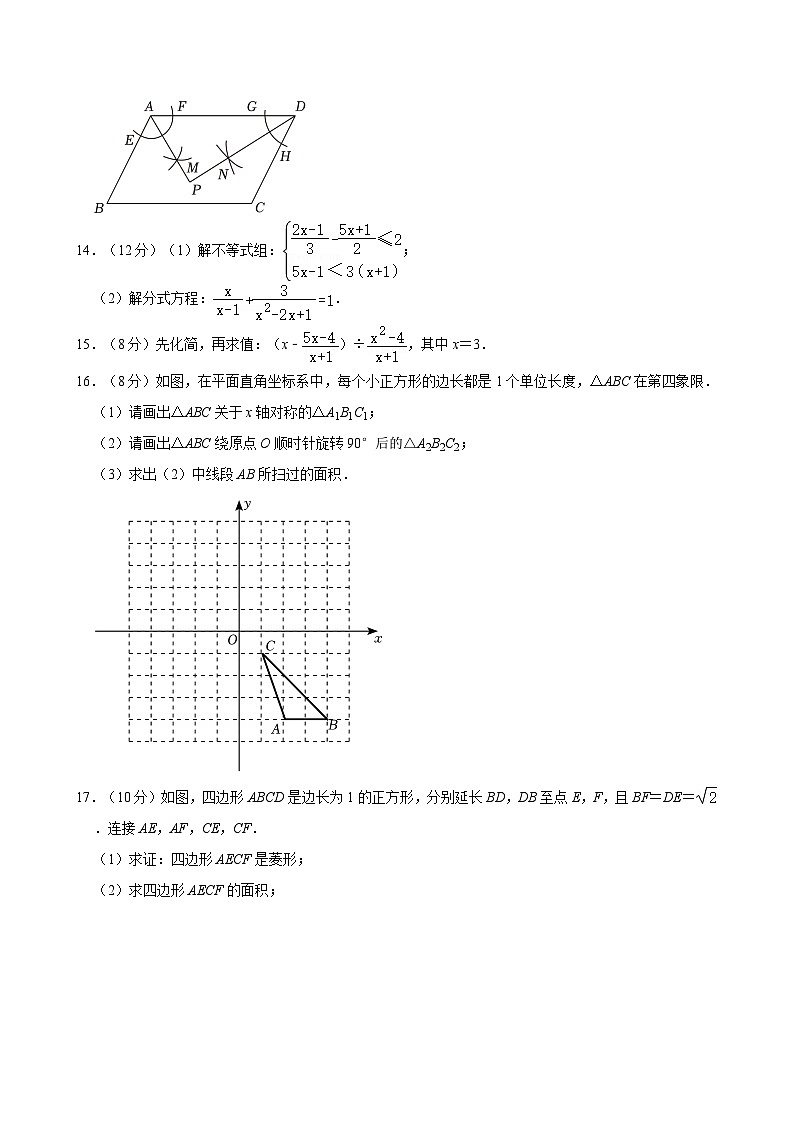
A．B．C．D．
6．（4分）将点P（2，3）向左平移2个单位，向上平移4个单位得到点Q，则点Q的坐标是（ ）
A．（4，7）B．（4，﹣1）C．（0，7）D．（0，﹣1）
7．（4分）如图，矩形ABCD中，O是对角线AC的中点，连接DO．若AB＝12，AD＝16，则DO的长为（ ）
A．7B．8C．9D．10
8．（4分）某化工厂要在规定时间内搬运2400千克化工原料，现有A，B两种机器人可供选择，已知B型机器人每小时完成的工作量是A型机器人的1.5倍，B型机器人单独完成所需的时间比A型机器人少16小时，如果设A型机器人每小时搬运x千克化工原料，则可以列出以下哪个方程（ ）
A．16（15x+x）＝2400B．16（15x﹣x）＝2400
C．D．
9．（4分）分解因式：8a2﹣2ab2＝ ．
10．（4分）如图，△ABC经过平移得到△A′B′C′，连接BB′、CC′，若BB′＝2.5cm，则点A与点A′之间的距离为 cm．
11．（4分）分式的值为0，则x＝ ．
12．（4分）如图所示，菱形ABCD的对角线AC、BD相交于点O．若AC＝6，BD＝8，AE⊥BC，垂足为E，则AE的长为 ．
13．（4分）如图，四边形ABCD是平行四边形，按以下步骤操作：①以点A为圆心，适当长为半径画弧，交AB于点E，交AD于点F；再分别以点E，F为圆心，以大于EF长为半径作弧，两弧相交于点M；②以点D为圆心，适当长为半径画弧，交CD于点H，交AD于点G；再分别以点G，H为圆心，以大于GH长为半径作弧，两弧相交于点N；③作射线AM，DN相交于点P．若AP＝4，BC＝8，则PD的长为 ．
14．（12分）（1）解不等式组：；
（2）解分式方程：．
15．（8分）先化简，再求值：（x﹣）÷，其中x＝3．
16．（8分）如图，在平面直角坐标系中，每个小正方形的边长都是1个单位长度，△ABC在第四象限．
（1）请画出△ABC关于x轴对称的△A1B1C1；
（2）请画出△ABC绕原点O顺时针旋转90°后的△A2B2C2；
（3）求出（2）中线段AB所扫过的面积．
17．（10分）如图，四边形ABCD是边长为1的正方形，分别延长BD，DB至点E，F，且BF＝DE＝．连接AE，AF，CE，CF．
（1）求证：四边形AECF是菱形；
（2）求四边形AECF的面积；
18．（10分）如图，在平面直角坐标系中，直线与x轴、y轴分别相交于A、B两点，点C在线段OA上，将线段CB绕着点C逆时针旋转90°得到线段CD，此时点D恰好落在直线AB上．
（1）求出线以AB的长度；
（2）求出BC的函数关系式；
（3）若点E是x轴上的一个动点，点F是线段CB上的点（不与点B、C重合），是否存在以C、D、E、F为顶点的四边形是平行四边形？若存在，求出所有满足条件的E点坐标；若不存在，说明理由．
二．B卷（共8小题，满分50分）
19．（4分）已知mn＝2，n+m＝3，则m2n+mn2＝ ．
20．（4分）若关于x的分式方程无解，则m的值为 ．
21．（4分）如图，一次函数与y＝﹣x+4的图象相交于点E（2，n），则关于x的不等式组的解集为 ．
22．（4分）如图，在Rt△ABC中，∠B＝90°，∠A＝30°，AB＝15，点D，E，F分别在边AB，BC，AC上，连接DE，EF，DF，若BD＝6，且△DEF是等边三角形，则CF＝ ．
23．（4分）如图，在菱形ABCD中，AB＝5，BD＝8，点P为线段BD上不与端点重合的一个动点．过点P作直线BC、直线CD的垂线，垂足分别为点E、点F．连结PA，在点P的运动过程中，PE+PA+PF的最小值等于 ．
24．（8分）某商店购进A，B两种商品共140件进行销售．已知采购A商品10件与B商品20件共170元，采购A商品20件与B商品30件共280元．
（1）求A，B商品每件进价分别是多少元？
（2）若该商店出售A，B两种商品时，先都以标价10元出售，售出一部分后再降价促销，都以标价的8折售完所有剩余商品．其中以10元售出的商品件数比购进A种商品件数少20件，该商店此次降价前后销售A，B两种商品共获利不少于360元，求商店至少购进A商品多少件？
（3）若采购这140件商品的费用不低于720元，不高于740元．然后将A商品每件加价2a元销售，B商品每件加价3a元销售，140件商品全部售出的最大利润为768元，请直接写出a的值．
25．（10分）如图1，在▱ABCD中，∠ABC的平分线交AD于点E，∠ADC的平分线交BC于点F．
（1）求证：四边形BEDF为平行四边形；
（2）如图2，连接EF，若EF⊥BC，BF＝8，EF＝4，求▱ABCD的面积；
（3）如图3，连接EF，作△EAB关于直线EF对称的△ECH，其中点A，B的对应点分别为点C，H，恰好有HE⊥DF，垂足为G．若EF＝，求BE的长．
26．（12分）如图，直线l：y＝kx+b（k≠0）与坐标轴分别交于点A，B，以OA为边在y轴的右侧作正方形AOBC，且S△AOB＝8．
（1）求直线l的解析式；
（2）如图1，点D是x轴上一动点，点E在AD的右侧，∠ADE＝90°，AD＝DE．
①当AE+CE最小时，求E点的坐标；
②如图2，点D是线段OB的中点，另一动点H在直线BE上，且∠HAC＝∠BAD，请求出点H的坐标．
四川省成都市金牛区铁路中学2024-2025学年九年级上学期数学开学考试试卷
参考答案与试题解析
A卷
1．（4分）下列图形既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
【答案】B
2．（4分）若a＞b，则下列不等式正确的是（ ）
A．﹣4a＞﹣4bB．a＞bC．4﹣a＞4﹣bD．a2＞b2
【答案】B
3．（4分）如图，在△ABC中，∠ABC，∠ACB的平分线交于点O，过点O作EF∥BC分别交AB，AC于点E，F，若AB＝5，AC＝4，则△AEF的周长是（ ）
A．8B．9C．10D．11
【答案】B
4．（4分）下列由左边到右边的变形，属于因式分解的是（ ）
A．B．a2﹣2a﹣1＝（a﹣1）2
C．x2+6x+10＝（x+3）2+1D．m2﹣4m＝m（m﹣4）
【答案】D
5．（4分）下列分式变形正确的是（ ）
A．B．C．D．
【答案】B
6．（4分）将点P（2，3）向左平移2个单位，向上平移4个单位得到点Q，则点Q的坐标是（ ）
A．（4，7）B．（4，﹣1）C．（0，7）D．（0，﹣1）
【答案】C
7．（4分）如图，矩形ABCD中，O是对角线AC的中点，连接DO．若AB＝12，AD＝16，则DO的长为（ ）
A．7B．8C．9D．10
【答案】D
8．（4分）某化工厂要在规定时间内搬运2400千克化工原料，现有A，B两种机器人可供选择，已知B型机器人每小时完成的工作量是A型机器人的1.5倍，B型机器人单独完成所需的时间比A型机器人少16小时，如果设A型机器人每小时搬运x千克化工原料，则可以列出以下哪个方程（ ）
A．16（15x+x）＝2400B．16（15x﹣x）＝2400
C．D．
【答案】C
9．（4分）分解因式：8a2﹣2ab2＝ 2a（4a﹣b2） ．
【答案】2a（4a﹣b2）．
10．（4分）如图，△ABC经过平移得到△A′B′C′，连接BB′、CC′，若BB′＝2.5cm，则点A与点A′之间的距离为 2.5 cm．
【答案】2.5．
11．（4分）分式的值为0，则x＝ 3 ．
【答案】见试题解答内容
12．（4分）如图所示，菱形ABCD的对角线AC、BD相交于点O．若AC＝6，BD＝8，AE⊥BC，垂足为E，则AE的长为 ．
【答案】见试题解答内容
13．（4分）如图，四边形ABCD是平行四边形，按以下步骤操作：①以点A为圆心，适当长为半径画弧，交AB于点E，交AD于点F；再分别以点E，F为圆心，以大于EF长为半径作弧，两弧相交于点M；②以点D为圆心，适当长为半径画弧，交CD于点H，交AD于点G；再分别以点G，H为圆心，以大于GH长为半径作弧，两弧相交于点N；③作射线AM，DN相交于点P．若AP＝4，BC＝8，则PD的长为 4 ．
【答案】4．
14．（12分）（1）解不等式组：；
（2）解分式方程：．
【答案】（1）（2）x＝﹣2．
15．（8分）先化简，再求值：（x﹣）÷，其中x＝3．
【答案】见试题解答内容
16．（8分）如图，在平面直角坐标系中，每个小正方形的边长都是1个单位长度，△ABC在第四象限．
（1）请画出△ABC关于x轴对称的△A1B1C1；
（2）请画出△ABC绕原点O顺时针旋转90°后的△A2B2C2；
（3）求出（2）中线段AB所扫过的面积．
【答案】（1）（2）见解析；（3）3π．
17．（10分）如图，四边形ABCD是边长为1的正方形，分别延长BD，DB至点E，F，且BF＝DE＝．连接AE，AF，CE，CF．
（1）求证：四边形AECF是菱形；
（2）求四边形AECF的面积；
【答案】见试题解答内容
18．（10分）如图，在平面直角坐标系中，直线与x轴、y轴分别相交于A、B两点，点C在线段OA上，将线段CB绕着点C逆时针旋转90°得到线段CD，此时点D恰好落在直线AB上．
（1）求出线以AB的长度；
（2）求出BC的函数关系式；
（3）若点E是x轴上的一个动点，点F是线段CB上的点（不与点B、C重合），是否存在以C、D、E、F为顶点的四边形是平行四边形？若存在，求出所有满足条件的E点坐标；若不存在，说明理由．
【答案】（1）3；
（2）y＝3x﹣3；
（3）存在，E点坐标（，0）或（﹣，0）．
二．B卷（共8小题，满分50分）
19．（4分）已知mn＝2，n+m＝3，则m2n+mn2＝ 6 ．
【答案】6．
20．（4分）若关于x的分式方程无解，则m的值为 0或2 ．
【答案】见试题解答内容
21．（4分）如图，一次函数与y＝﹣x+4的图象相交于点E（2，n），则关于x的不等式组的解集为 2≤x＜4 ．
【答案】2≤x＜4．
22．（4分）如图，在Rt△ABC中，∠B＝90°，∠A＝30°，AB＝15，点D，E，F分别在边AB，BC，AC上，连接DE，EF，DF，若BD＝6，且△DEF是等边三角形，则CF＝ 3 ．
【答案】3．
23．（4分）如图，在菱形ABCD中，AB＝5，BD＝8，点P为线段BD上不与端点重合的一个动点．过点P作直线BC、直线CD的垂线，垂足分别为点E、点F．连结PA，在点P的运动过程中，PE+PA+PF的最小值等于 7.8 ．
【答案】见试题解答内容
24．（8分）某商店购进A，B两种商品共140件进行销售．已知采购A商品10件与B商品20件共170元，采购A商品20件与B商品30件共280元．
（1）求A，B商品每件进价分别是多少元？
（2）若该商店出售A，B两种商品时，先都以标价10元出售，售出一部分后再降价促销，都以标价的8折售完所有剩余商品．其中以10元售出的商品件数比购进A种商品件数少20件，该商店此次降价前后销售A，B两种商品共获利不少于360元，求商店至少购进A商品多少件？
（3）若采购这140件商品的费用不低于720元，不高于740元．然后将A商品每件加价2a元销售，B商品每件加价3a元销售，140件商品全部售出的最大利润为768元，请直接写出a的值．
【答案】（1）A商品每件的进价为5元，B商品每件的进价为6元；
（2）至少购进A商品40件；
（3）a的值为2.4．
25．（10分）如图1，在▱ABCD中，∠ABC的平分线交AD于点E，∠ADC的平分线交BC于点F．
（1）求证：四边形BEDF为平行四边形；
（2）如图2，连接EF，若EF⊥BC，BF＝8，EF＝4，求▱ABCD的面积；
（3）如图3，连接EF，作△EAB关于直线EF对称的△ECH，其中点A，B的对应点分别为点C，H，恰好有HE⊥DF，垂足为G．若EF＝，求BE的长．
【答案】（1）证明见解答；
（2）∴▱ABCD的面积为52；
（3）BE的长为2+．
26．（12分）如图，直线l：y＝kx+b（k≠0）与坐标轴分别交于点A，B，以OA为边在y轴的右侧作正方形AOBC，且S△AOB＝8．
（1）求直线l的解析式；
（2）如图1，点D是x轴上一动点，点E在AD的右侧，∠ADE＝90°，AD＝DE．
①当AE+CE最小时，求E点的坐标；
②如图2，点D是线段OB的中点，另一动点H在直线BE上，且∠HAC＝∠BAD，请求出点H的坐标．
【答案】（1）y＝﹣x+4；
（2）①点E（，）；②点H坐标为（12，8）或（6，2）．