北师大版八年级数学上册专题7.6三角形中的八大经典模型同步练习(学生版+解析)

这是一份北师大版八年级数学上册专题7.6三角形中的八大经典模型同步练习(学生版+解析)，共56页。


TOC \ "1-3" \h \u
\l "_Tc27912" 【题型1 A字模型】 PAGEREF _Tc27912 \h 1
\l "_Tc8458" 【题型2 8字模型】 PAGEREF _Tc8458 \h 3
\l "_Tc20902" 【题型3 双垂直模型】 PAGEREF _Tc20902 \h 4
\l "_Tc2975" 【题型4 飞镖模型】 PAGEREF _Tc2975 \h 6
\l "_Tc9529" 【题型5 风筝模型】 PAGEREF _Tc9529 \h 8
\l "_Tc16648" 【题型6 两内角角平分线模型】 PAGEREF _Tc16648 \h 9
\l "_Tc13875" 【题型7 两外角角平分线模型】 PAGEREF _Tc13875 \h 11
\l "_Tc13727" 【题型8 内外角角平分线模型】 PAGEREF _Tc13727 \h 14
【知识点1 A字模型】
【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，
∴∠AED+∠ADE=∠B+C，得证.
【题型1 A字模型】
【例1】（2023春·湖北荆门·八年级校联考期末）如图，在△ABC中，∠C＝70º，沿图中虚线截去∠C，则∠1＋∠2＝（ ）
A．360ºB．250ºC．180ºD．140º
【变式1-1】（2023春·八年级单元测试）如图所示，∠DAE的两边上各有一点B,C，连接BC，求证∠DBC+∠ECB=180°+∠A．
【变式1-2】（2023春•常州期中）如图，△ABC中，∠B＝68°，∠A比∠C大28°，点D、E分别在AB、BC上．连接DE，∠DEB＝42°．
（1）求∠A的度数；
（2）判断DE与AC之间的位置关系，并说明理由．
【变式1-3】（2023春·江苏泰州·八年级校联考期中）如图，已知∠A=40°，则∠1+∠2+∠3+∠4的度数为 ．
【知识点2 8字模型】
【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中，由内角和定理：∠A+∠B+∠BOA=180°，在△CDO中，∠C+∠D+∠COD=180°，
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD，由对顶角相等：∠BOA=∠COD
∴∠A+∠B=∠C+∠D，得证.
【题型2 8字模型】
【例2】（2015-2016学年北京市怀柔区八年级上学期期末数学试卷（带解析））如图是由线段AB，CD，DF，BF，CA组成的平面图形，∠D=28∘，则∠A+∠B+∠C+∠F的度数为( )
A．62∘B．152∘C．208∘D．236∘
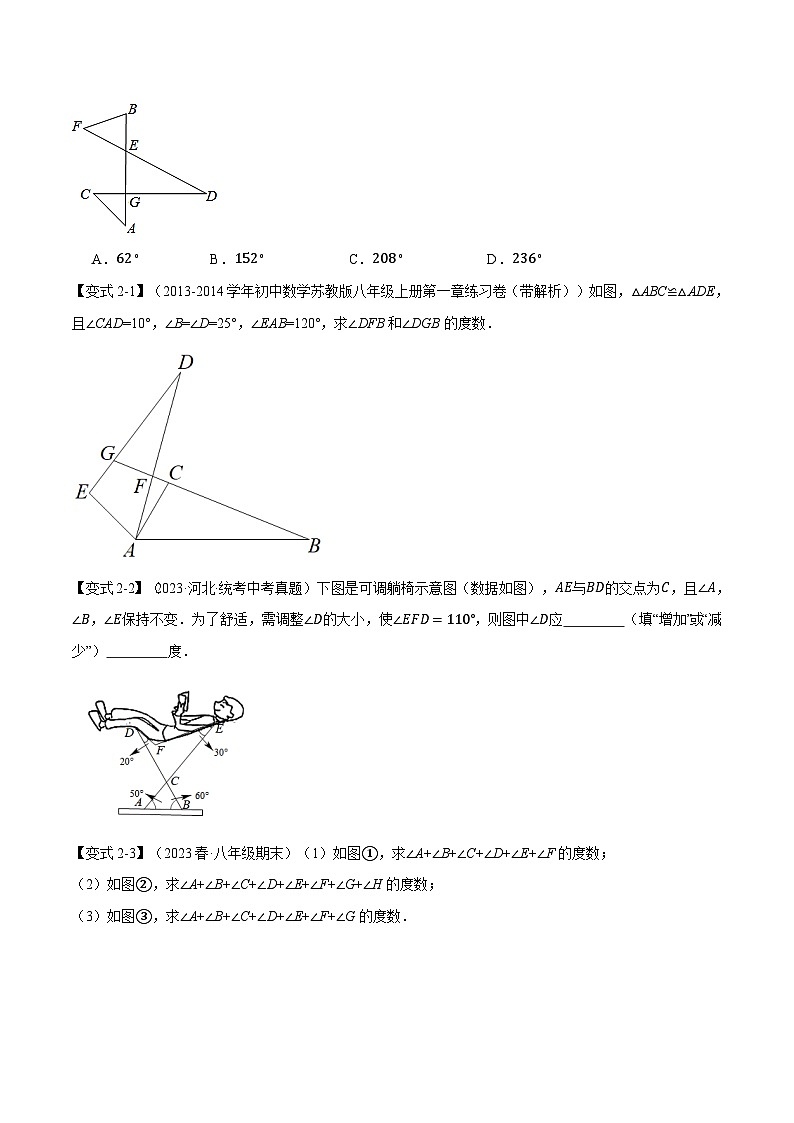
【变式2-1】（2013-2014学年初中数学苏教版八年级上册第一章练习卷（带解析））如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．
【变式2-2】（2023·河北·统考中考真题）下图是可调躺椅示意图（数据如图），AE与BD的交点为C，且∠A，∠B，∠E保持不变．为了舒适，需调整∠D的大小，使∠EFD=110°，则图中∠D应 （填“增加”或“减少”） 度．
【变式2-3】（2023春·八年级期末）（1）如图①，求∠A+∠B+∠C+∠D+∠E+∠F的度数；
（2）如图②，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数；
（3）如图③，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数．
【知识点3 双垂直模型】
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE，∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°；∴∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°，且∠CED+∠DCE =90°；∴∠ACB=∠CED，得证.
【题型3 双垂直模型】
【例3】（2023春·广东珠海·八年级校联考期末）如图1，线段AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．
（1）求证：∠EAB=∠CED；
（2）如图2，AF、DF分别平分∠BAE和∠CDE，EH平分∠DEC交CD于点H，EH的反向延长线交AF于点G．
①求证EG⊥AF；
②求∠F的度数．【提示：三角形内角和等于180度】
【变式3-1】（2023春·江苏泰州·八年级校考期中）如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE、CD相交于点F， 求证：∠CFE=∠CEF 请在以下的解题过程中的括号里填推理的理由．
证明：∵AE平分∠CAB（已知）
∴∠CAE=∠FAB（_____________________）
∵∠ACE=90°（已知）
∴∠CAE+∠CEF=90°（_____________________）
∵CD是△ABC的高（已知）
∴∠FDA=90°（三角形高的定义）
∴∠FAB+∠AFD=90°（直角三角形的两锐角互余）
∴∠CEF=∠AFD（____________________________）
∵∠CFE=∠AFD（_____________________）
∴∠CFE=∠CEF（____________________）
【变式3-2】（2023春·山东青岛·八年级山东省青岛第五十九中学校考期中）如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF交AD于点G．
(1)判断△DBF的形状，并说明理由．
(2)求证：AD⊥CF．
【变式3-3】（2023春·山东济南·八年级济南育英中学校联考期中）如图，△ABC中，∠B=90°，点D在射线BC上运动，DE⊥AD交射线AC于点E．
（1）如图1，若∠BAC=60°，当AD平分∠BAC时，求∠EDC的度数；
（2）如图2，当点D在线段BC上时，①判断∠EDC与∠BAD的数量关系并说明理由；
②作EF⊥BC于F，∠BAD、∠DEF的角平分线相交于点G，随着点D的运动，∠G的度数会变化吗？如果不变，求出∠G的度数；如果变化，说明理由；
（3）如图3，当点D在BC的延长线上时，作EF⊥BD于F，∠BAD的角平分线和∠DEF的角平分线的反向延长线相交于点G，∠G的度数会变化吗？如果不变，求出∠G的度数；如果变化，说明理由．
【知识点4 飞镖模型】
【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图，连接AD并延长到E，则：
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
【题型4 飞镖模型】
【例4】（2023春·江苏镇江·八年级统考期中）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果∠A=52°,∠B=25°，∠C=30°,∠D=35°,∠E=72°，那么∠F的度数是（ ）．
A．72°B．70°C．65°D．60°
【变式4-1】（2023春·八年级期末）如图，已知在△ABC中，∠A=40°，现将一块直角三角板放在△ABC上，使三角板的两条直角边分别经过点B,C，直角顶点D落在△ABC的内部，则∠ABD+∠ACD=（ ）．
A．90°B．60°C．50°D．40°
【变式4-2】（2023·全国·八年级假期作业）如图所示，已知四边形ABDC，求证∠BDC=∠A+∠B+∠C．
【变式4-3】（2023春·福建南平·八年级统考期中）如图，若∠EOC=115°，则∠A+∠B+∠C+∠D+∠E+∠F= ．
【知识点5 风筝模型】

【条件】四边形ABPC，分别延长AB、AC于点D、E，如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图，连接AP，则：∠PBD=∠PAB+∠APB，∠PCE=∠PAC+∠APC，
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC，得证.
【题型5 风筝模型】
【例5】（2023春·重庆渝北·八年级校考期中）如图,将△ABC沿着DE翻折,使B点与B'点重合,若∠1+∠2=80°,则∠B的度数为（ ）
A．20°B．30°C．40°D．50°
【变式5-1】（2023春·八年级期末）如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A＝55°，∠1＝95°，则∠2的度数为（ ）．
A．14°B．15°C．28°D．30°
【变式5-2】（2023春·八年级期末）如图，三角形纸片ABC中，∠A=65°,∠B=75°，将∠C沿DE翻折，使点C落在△ABC外的点C'处．若∠1=20°，则∠2的度数为 ．
【变式5-3】（2023春·全国·八年级专题练习）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝120°，则∠1+∠2的度数为（ ）
A．90°B．100°C．110°D．120°
【知识点6 两内角角平分线模型】
【条件】△ABC中，BI、CI分别是∠ABC和∠ACB的角平分线，且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线，∴∵CI是∠ACB平分线，∴
由A→B→I→C→A的飞镖模型可知：
∠I=∠A+∠2+∠3=∠A++=∠A+=.
【题型6 两内角角平分线模型】
【例6】（2023春·江苏苏州·八年级期中）直线MN与直线PQ垂直相交于点O，点A在直线PQ上运动，点B在直线MN上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出∠CED的度数．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及反向延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，则∠ABO的度数为____（直接写答案）
【变式6-1】（2023春·全国·八年级专题练习）如图，BE平分∠ABD，CF平分∠ACD，BE与CF交于点G，若∠BDC=140°，∠BGC=100°，则∠A=（ ）
A．80°B．75°C．60°D．45°
【变式6-2】（2023春·全国·八年级专题练习）如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，延长BO与∠ACB的外角平分线交于点D，若∠BOC＝130°，则∠D＝
【变式6-3】（2023春·黑龙江哈尔滨·八年级校联考期末）如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．
（1）若∠MON=60°，则∠ACG= ；（直接写出答案）
（2）若∠MON=n°，求出∠ACG的度数；（用含n的代数式表示）
（3）如图2，若∠MON=80°，过点C作CF∥OA交AB于点F，求∠BGO与∠ACF的数量关系．
【知识点7 两外角角平分线模型】
【条件】△ABC中，BI、CI分别是△ABC的外角的角平分线，且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线，∴，∵CO是∠FCB平分线，∴
由△BCO中内角和定理可知：
∠O=180°-∠2-∠5=180°--=180°--===
【题型7 两外角角平分线模型】
【例7】（2023春·江苏·八年级专题练习）【问题背景】
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
【简单应用】
（2）如图2， AP、CP分别平分∠BAD． ∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；
【问题探究】
（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．
【拓展延伸】
（4） ①在图4中，若设∠C=α，∠B=β，∠CAP=13∠CAB，∠CDP=13∠CDB，试问∠P与∠C、∠B之间的数量关系为： （用α、β表示∠P）；
②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE， 猜想∠P与∠B、∠D的关系，直接写出结论．
【变式7-1】（2023春·全国·八年级专题练习）如图，五边形ABCDE在∠BCD,∠EDC处的外角分别是∠FCD,∠GDC,CP,DP分别平分∠FCD和∠GDC且相交于点P．若∠A=160°,∠B=80°,∠E=90°，则∠CPD= ．
【变式7-2】（2023春·全国·八年级专题练习）如图，点P是ΔABC的外角∠BCE和∠CBF的角平分线交点，延长BP交AC于G，请写出∠A和∠CPG的数量关系.
【变式7-3】（2023春·八年级期末）如图1，△ABC的外角平分线交于点F．
（1）若∠A＝40°，则∠F的度数为 ；
（2）如图2，过点F作直线MN∥BC，交AB，AC延长线于点M，N，若设∠MFB＝α，∠NFC＝β，则∠A与α+β的数量关系是 ；
（3）在（2）的条件下，将直线MN绕点F转动．
①如图3，当直线MN与线段BC没有交点时，试探索∠A与α，β之间的数量关系，并说明理由；
②当直线MN与线段BC有交点时，试问①中∠A与α，β之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请给出三者之间的数量关系．
【知识点8 内外角角平分线模型】
【条件】△ABC中，BP、CP分别是△ABC的内角和外角的角平分线，且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线，∴ ∵CP是∠ACE平分线，∴
由△ABC外角定理可知：∠ACE=∠ABC+∠A即：2∠1=2∠3+∠A ……①
对①式两边同时除以2，得：∠1=∠3+ ……②又在△BPC中由外角定理可知：∠1=∠3+∠P ……③
比较②③式子可知：.==.
【题型8 内外角角平分线模型】
【例8】（2023春·八年级期末）如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD的平分线，CA3是∠A2CD的平分线，……以此类推，若∠A=α，则∠A2020= ．
【变式8-1】（2023春·八年级期末）如图，已知△ABC的两条高BD、CE交于点F，∠ABC的平分线与△ABC外角∠ACM的平分线交于点G，若∠BFC=8∠G，则∠A= °．
【变式8-2】（2023春·八年级期末）如图，在△ABC中，∠A=60°，BD、CD分别平分∠ABC、∠ACB，M、N、Q分别在DB、DC、BC的延长线上，BE、CE分别平分∠MBC、∠BCN，BF、CF分别平分∠EBC、∠ECQ，则∠F= ．
【变式8-3】（2023春·江苏南通·八年级南通田家炳中学校考期末）在△ABC中，若存在一个内角角度是另外一个内角角度的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝75°，∠C＝25°，可知∠B＝3∠C，所以△ABC为3倍角三角形．
（1）在△ABC中，∠A＝80°，∠B＝60°，则△ABC为 倍角三角形；
专题7.6 三角形中的八大经典模型
【北师大版】
TOC \ "1-3" \h \u
\l "_Tc27912" 【题型1 A字模型】 PAGEREF _Tc27912 \h 1
\l "_Tc8458" 【题型2 8字模型】 PAGEREF _Tc8458 \h 4
\l "_Tc20902" 【题型3 双垂直模型】 PAGEREF _Tc20902 \h 8
\l "_Tc2975" 【题型4 飞镖模型】 PAGEREF _Tc2975 \h 16
\l "_Tc9529" 【题型5 风筝模型】 PAGEREF _Tc9529 \h 21
\l "_Tc16648" 【题型6 两内角角平分线模型】 PAGEREF _Tc16648 \h 24
\l "_Tc13875" 【题型7 两外角角平分线模型】 PAGEREF _Tc13875 \h 30
\l "_Tc13727" 【题型8 内外角角平分线模型】 PAGEREF _Tc13727 \h 38
【知识点1 A字模型】
【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，
∴∠AED+∠ADE=∠B+C，得证.
【题型1 A字模型】
【例1】（2023春·湖北荆门·八年级校联考期末）如图，在△ABC中，∠C＝70º，沿图中虚线截去∠C，则∠1＋∠2＝（ ）
A．360ºB．250ºC．180ºD．140º
【答案】B
【分析】根据三角形内角和定理得出∠A+∠B=110°，进而利用四边形内角和定理得出答案．
【详解】解：∵△ABC中，∠C=70°，
∴∠A+∠B=180°-∠C，
∴∠1+∠2=360°-110°=250°，
【点睛】本题主要考查了多边形内角和定理，根据题意得出∠A+∠B的度数是解题关键．
【变式1-1】（2023春·八年级单元测试）如图所示，∠DAE的两边上各有一点B,C，连接BC，求证∠DBC+∠ECB=180°+∠A．
【答案】见解析
【分析】根据三角形的外角等于与它不相邻的两个内角的和证明即可．
【详解】解：∵∠DBC和∠ECB是△ABC的外角，
∴∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC．
又∵∠A+∠ABC+∠ACB=180°，
∴∠DBC+∠ECB=∠A+∠ACB+∠ABC+∠A=180°+∠A．
【点睛】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．
【变式1-2】（2023春•常州期中）如图，△ABC中，∠B＝68°，∠A比∠C大28°，点D、E分别在AB、BC上．连接DE，∠DEB＝42°．
（1）求∠A的度数；
（2）判断DE与AC之间的位置关系，并说明理由．
【分析】（1）设∠C的度数为x，根据三角形的内角和列出方程解答即可；
（2）根据平行线的判定解答即可．
【详解】解：（1）设∠C的度数为x°，则∠A的度数为（x+28）°，
△ABC中，∠A+∠B+∠C＝180°，∠B＝68°，
可得：x+x+28+68＝180，
解得：x＝42，
所以∠C＝42°，∠A＝70°，
（2）∵∠DEB＝42°，∠C＝42°，
∴∠DEB＝∠C，
∴DE∥AC．
【变式1-3】（2023春·江苏泰州·八年级校联考期中）如图，已知∠A=40°，则∠1+∠2+∠3+∠4的度数为 ．
【答案】280°
【分析】根据三角形的内角和定理分别求得∠1+∠2，∠3+∠4，就可求得最后结果．
【详解】∵∠A=40°，
∴∠1+∠2=∠3+∠4=180°-∠A=140°，
∴∠1+∠2+∠3+∠4=280°，
故答案为280°．
【点睛】本题考查了三角形内角和定理的运用，熟练掌握三角形内角和为180度是解题的关键．
【知识点2 8字模型】
【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中，由内角和定理：∠A+∠B+∠BOA=180°，在△CDO中，∠C+∠D+∠COD=180°，
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD，由对顶角相等：∠BOA=∠COD
∴∠A+∠B=∠C+∠D，得证.
【题型2 8字模型】
【例2】（2015-2016学年北京市怀柔区八年级上学期期末数学试卷（带解析））如图是由线段AB，CD，DF，BF，CA组成的平面图形，∠D=28∘，则∠A+∠B+∠C+∠F的度数为( )
A．62∘B．152∘C．208∘D．236∘
【答案】A
【详解】∵如图可知∠BED=∠F+∠B，∠CGE=∠C+∠A，
又∵∠BED=∠D+∠EGD，
∴∠F+∠B=∠D+∠EGD，
又∵∠CGE+∠EGD=180°，
∴∠C+∠A+∠F+∠B−∠D=180°，
又∵∠D=28°，
∴∠A+∠B+∠C+∠F=180°+28°=208°，
故选C．
点睛：本题主要考查了三角形内角和定理即三角形外角与内角的关系，解答本题的关键是求出∠C+∠A+∠F+∠B﹣∠D=180°，此题难度不大．
【变式2-1】（2013-2014学年初中数学苏教版八年级上册第一章练习卷（带解析））如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．
【答案】90°；65°
【分析】由ΔABC≅ΔADE，可得∠DAE=∠BAC=12(∠EAB−∠CAD)，根据三角形外角性质可得∠DFB=∠FAB+∠B，因为∠FAB=∠FAC+∠CAB，即可求得∠DFB的度数；根据三角形内角和定理可得∠DGB=∠DFB−∠D，即可得∠DGB的度数．
【详解】解：∵ΔABC≅ΔADE，
∴∠DAE=∠BAC=12(∠EAB−∠CAD)=12(120°−10°)=55°．
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB−∠D=90°−25°=65°．
综上所述：∠DFB=90°，∠DGB=65°．
【点睛】本题主要考查三角形全等的性质，解题的关键是找到相应等量关系的角，做题时要结合图形进行思考．
【变式2-2】（2023·河北·统考中考真题）下图是可调躺椅示意图（数据如图），AE与BD的交点为C，且∠A，∠B，∠E保持不变．为了舒适，需调整∠D的大小，使∠EFD=110°，则图中∠D应 （填“增加”或“减少”） 度．
【答案】 减少 10
【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系，进行计算即可判断．
【详解】解：∵∠A+∠B=50°+60°=110°，
∴∠ACB=180°-110°=70°，
∴∠DCE=70°，
如图，连接CF并延长，
∴∠DFM=∠D+∠DCF=20°+∠DCF，
∠EFM=∠E+∠ECF=30°+∠ECF，
∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°，
要使∠EFD=110°，则∠EFD减少了10°，
若只调整∠D的大小，
由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠ D+100°，
因此应将∠D减少10度；
故答案为：①减少；②10．
【点睛】本题考查了三角形外角的性质，同时涉及到了三角形的内角和与对顶角相等的知识；解决本题的关键是理解题意，读懂图形，找出图形中各角之间的关系以及牢记公式建立等式求出所需的角，本题蕴含了数形结合的思想方法．
【变式2-3】（2023春·八年级期末）（1）如图①，求∠A+∠B+∠C+∠D+∠E+∠F的度数；
（2）如图②，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数；
（3）如图③，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数．
【答案】（1）360°；（2）720°；（3）540°
【分析】（1）连接AD，根据三角形的内角和定理得∠B＋∠C＝∠BAD＋∠CDA，进而将问题转化为求四边形ADEF的内角和，
（2）与（1）方法相同转化为求六边形ABCDEF的内角和，
（3）使用上述方法，转化为求五边形ABCDE的内角和．
【详解】解：（1）如图①，连接AD，
由三角形的内角和定理得，∠B＋∠C＝∠BAD＋∠CDA，
∴∠BAF＋∠B＋∠C＋∠CDE＋∠E＋∠F＝∠BAF＋∠BAD＋∠CDA＋∠D＋∠E＋∠F
即四边形ADEF的内角和，四边形的内角和为360°，
∴∠BAF＋∠B＋∠C＋∠CDE＋∠E＋∠F＝360°，
（2）如图②，由（1）方法可得：
∠BAH＋∠B＋∠C＋∠D＋∠E＋∠EFG＋∠G＋∠H的度数等于六边形ABCDEF的内角和，
∴∠BAH＋∠B＋∠C＋∠D＋∠E＋∠EFG＋∠G＋∠H＝（6－2）×180°＝720°，
（3）如图③，根据（1）的方法得，∠F＋∠G＝∠GAE＋∠FEA，
∠BAG＋∠B＋∠C＋∠D＋∠DEF＋∠F＋∠G的度数等于五边形ABCDE的内角和，
∴∠BAG＋∠B＋∠C＋∠D＋∠DEF＋∠F＋∠G＝（5－2）×180°＝540°，
【点睛】本题考查三角形的内角和、多边形的内角和的计算方法，适当的转化是解决问题的关键．
【知识点3 双垂直模型】
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE，∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°；∴∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°，且∠CED+∠DCE =90°；∴∠ACB=∠CED，得证.
【题型3 双垂直模型】
【例3】（2023春·广东珠海·八年级校联考期末）如图1，线段AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．
（1）求证：∠EAB=∠CED；
（2）如图2，AF、DF分别平分∠BAE和∠CDE，EH平分∠DEC交CD于点H，EH的反向延长线交AF于点G．
①求证EG⊥AF；
②求∠F的度数．【提示：三角形内角和等于180度】
【答案】（1）证明见解析；（2）①证明见解析；②45°．
【分析】（1）利用同角的余角相等即可证明；
（2）①想办法证明∠EAG+∠AEG=90°即可解决问题；
②利用∠DFA=∠DFM+∠AFM=12∠CDE+12∠EAB=12（∠CDE+∠EAB）即可解决问题.
【详解】（1）∵AB⊥BC，
∴∠EAB+∠AEB=90°，
∵AE⊥ED，
∴∠CED+∠AEB=90°，
∴∠EAB=∠CED．
（2）①∵AF平分∠BAE，
∴∠EAG=12∠EAB，
∵EH平分∠DEC，
∴∠HED=12∠CED，
∵∠EAB=∠CED，
∴∠HED=∠EAG，
∴∠HED+∠AEG=90°，
∴∠EAG+∠AEG=90°，
∴∠EGA=90°，
∴EG⊥AF．
②作FM∥CD，
∵AB⊥BC，CD⊥BC，
∴AB∥CD，
∴FM∥AB，
∴∠DFM=∠CDF=12∠CDE，∠AFM=∠FAB=12∠EAB，
∵∠CDE+∠CED=90°，
∴∠CDE+∠EAB=90°，
∴∠DFA=∠DFM+∠AFM=12∠CDE+12∠EAB=12（∠CDE+∠EAB）=45°．
【点睛】本题考查三角形内角和定理、平行线的性质、角平分线的定义等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．
【变式3-1】（2023春·江苏泰州·八年级校考期中）如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE、CD相交于点F， 求证：∠CFE=∠CEF 请在以下的解题过程中的括号里填推理的理由．
证明：∵AE平分∠CAB（已知）
∴∠CAE=∠FAB（_____________________）
∵∠ACE=90°（已知）
∴∠CAE+∠CEF=90°（_____________________）
∵CD是△ABC的高（已知）
∴∠FDA=90°（三角形高的定义）
∴∠FAB+∠AFD=90°（直角三角形的两锐角互余）
∴∠CEF=∠AFD（____________________________）
∵∠CFE=∠AFD（_____________________）
∴∠CFE=∠CEF（____________________）
【答案】角平分线的定义；直角三角形的两锐角互余；等角的余角相等；对顶角相等；等量代换
【分析】根据角平分线的定义得到∠CAE=∠FAB，根据直角三角形两锐角互余得到∠CAE+∠CEF=90°，∠FAB+∠AFD=90°，再利用等角的余角相等得到∠CEF=∠AFD，最后利用等量代换可得结果．
【详解】解：证明：∵AE平分∠CAB（已知）
∴∠CAE=∠FAB（角平分线的定义）
∵∠ACE=90°（已知）
∴∠CAE+∠CEF=90°（直角三角形的两锐角互余）
∵CD是△ABC的高（已知）
∴∠FDA=90°（三角形高的定义）
∴∠FAB+∠AFD=90°（直角三角形的两锐角互余）
∴∠CEF=∠AFD（等角的余角相等）
∵∠CFE=∠AFD（对顶角相等）
∴∠CFE=∠CEF（等量代换）
故答案为：角平分线的定义；直角三角形的两锐角互余；等角的余角相等；对顶角相等；等量代换
【点睛】本题考查的是三角形内角和定理，角平分线的定义，余角的性质，熟知三角形内角和是180°是解答此题的关键，此题难度不大．
【变式3-2】（2023春·山东青岛·八年级山东省青岛第五十九中学校考期中）如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF交AD于点G．
(1)判断△DBF的形状，并说明理由．
(2)求证：AD⊥CF．
【答案】(1)△DBF是等腰直角三角形，理由见解析；
(2)证明见解析．
【分析】（1）利用等腰Rt△ABC中，∠ACB=90°，证明∠CBA=∠CAB=45°，再利用BF∥AC得到∠ABF=∠CAB=45°，进一步得∠CBA+∠ABF=90°，利用DE⊥AB证明∠BDF=45°即可证明△DBF是等腰直角三角形；
（2）欲求证AD⊥CF，先证明∠CAG+∠ACG＝90°，需证明∠CAG＝∠BCF，只要证明三角形全等，即可．
【详解】（1）解：△DBF是等腰直角三角形，理由如下：
∵等腰Rt△ABC中，∠ACB=90°，
∴∠CBA=∠CAB=45°，
∵BF∥AC，
∴∠ABF=∠CAB=45°，
∴∠CBA+∠ABF=90°，即∠DBF=90°，
∵DE⊥AB，∠CBA=45°，
∴∠BDF=45°，
∴∠BFD=45°，
∴△DBF是等腰直角三角形．
（2）证明：在等腰直角三角形ABC中，
∵∠ACB＝90°，
∴∠CBA＝∠CAB＝45°．
又∵DE⊥AB，
∴∠DEB＝90°．
∴∠BDE＝45°．
又∵BF∥AC，
∴∠CBF＝90°．
∴∠BFD＝45°＝∠BDE．
∴BF＝DB．
又∵D为BC的中点，
∴CD＝DB．
∴BF＝CD．
在△CBF和△ACD中，
BF=CD∠CBF=∠ACDCB=AC
∴△CBF≌△ACD（SAS）．
∴∠BCF＝∠CAD．
又∵∠BCF+∠GCA＝90°，
∴∠CAD+∠GCA＝90°．
∴∠AGC=90°，
即AD⊥CF．
【点睛】本题考查了三角形的综合问题，掌握全等三角形的性质以及判定定理、垂直的定义、等腰三角形的性质以及判定是解题的关键．
【变式3-3】（2023春·山东济南·八年级济南育英中学校联考期中）如图，△ABC中，∠B=90°，点D在射线BC上运动，DE⊥AD交射线AC于点E．
（1）如图1，若∠BAC=60°，当AD平分∠BAC时，求∠EDC的度数；
（2）如图2，当点D在线段BC上时，①判断∠EDC与∠BAD的数量关系并说明理由；
②作EF⊥BC于F，∠BAD、∠DEF的角平分线相交于点G，随着点D的运动，∠G的度数会变化吗？如果不变，求出∠G的度数；如果变化，说明理由；
（3）如图3，当点D在BC的延长线上时，作EF⊥BD于F，∠BAD的角平分线和∠DEF的角平分线的反向延长线相交于点G，∠G的度数会变化吗？如果不变，求出∠G的度数；如果变化，说明理由．
【答案】（1）30°；（2）①∠EDC=∠BAD，理由见解析；②∠G的度数不变， 理由见解析；（3）不变，45°.
【分析】（1）先求出∠ACB=30°，再利用角平分线得出∠DAC=30°，即可得出∠ADC=120°即可得出结论；
（2）①利用直角三角形的两锐角互余和等角的余角相等即可得出结论； ②先利用①的结论得出∠BAD+∠DEF=90°，进而得出∠DAG+∠DEG=45°，最后利用三角形的内角和即可得出结论；
（3）利用三角形的外角和三角形的内角和即可得出结论．
【详解】解：（1）在Rt△ABC中，∠BAC=60°，
∴∠ACB=30°，
∵AD平分∠BAC，
∴∠DAC=12∠BAC=30°，
∴∠ADC=120°，
∵DE⊥AD，
∴∠ADE=90°，
∴∠EDC=∠ADC-∠ADE=30°；
（2）①相等，
在Rt△ABD中，∠BAD+∠ADB=90°，
∵∠ADE=90°，
∴∠EDC+∠ADB=90°，
∴∠EDC=∠BAD；
②∠G的度数不变， 理由：∵EF⊥BC，
∴∠EDF+∠DEF=90°，
∵∠ADB+∠EDF=90°，
∴∠ADB=∠DEF，
∵∠BAD+∠ADB=90°，
∴∠BAD+∠DEF=90°，
∵∠BAD、∠DEF的角平分线相交于点G，
∴∠DAG=12∠BAD，∠DEG=12∠DEF，
∴∠DAG+∠DEG=12（∠BAD+∠DEF）=45°，
∵∠DAE+∠DEA=90°，
∴∠GAE+∠GEA=90°+45°=135°，
∴∠G=45°；
（3）∠G的度数不变化，
理由：如图3，
∵AD⊥DE，
∴∠ADB+∠BDE=90°，
∵EF⊥BD，
∴∠DEF+∠BDE=90°，
∴∠ADB=∠DEF，
∵EM是∠DEF的角平分线，
∴∠DEM=12∠DEF=12∠ADB，
∵AG平分∠BAD，
∴∠DAG=12∠BAD， 延长DE交AG于N，
∴∠AEN=∠ADE+∠DAE=90°+∠DAE，
∴∠ENG=∠AEN+∠EAG =90°+∠DAE+∠EAG =90°+∠DAG =90°+12∠BAD，
∴∠G=180°-（∠ENG+∠GEN） =180°-（∠ENG+∠DEM），
=180°-（90°+12∠BAD+ 12∠ADB），
=90°-12（∠BAD+∠ADB） =45°．
【点睛】本题主要考查了角平分线的定义，直角三角形的性质，三角形的内角和和外角的性质，解（1）的关键是求出∠ADC=120°，解（2）的关键是求出∠DAG+∠DEG=45°，解（3）的关键是利用三角形的外角的性质．
【知识点4 飞镖模型】
【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图，连接AD并延长到E，则：
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
【题型4 飞镖模型】
【例4】（2023春·江苏镇江·八年级统考期中）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果∠A=52°,∠B=25°，∠C=30°,∠D=35°,∠E=72°，那么∠F的度数是（ ）．
A．72°B．70°C．65°D．60°
【答案】B
【分析】延长BE交CF的延长线于O，连接AO，根据三角形内角和定理求出∠BOC,再利用邻补角的性质求出∠DEO，再根据四边形的内角和求出∠DFO，根据邻补角的性质即可求出∠DFC的度数．
【详解】延长BE交CF的延长线于O，连接AO，如图，
∵∠OAB+∠B+∠AOB=180°,
∴∠AOB=180°−∠B−∠OAB,
同理得∠AOC=180°−∠OAC−∠C,
∵∠AOB+∠AOC+∠BOC=360°,
∴∠BOC=360°−∠AOB−∠AOC
=360°−(180°−∠B−∠OAB)−(180°−∠OAC−∠C)
=∠B+∠C+∠BAC=107°,
∵∠BED=72°,
∴∠DEO=180°−∠BED=108°,
∴∠DFO=360°−∠D−∠DEO−∠EOF
=360°−35°−108°−107°=110°,
∴∠DFC=180°−∠DFO=180°−110°=70°,
【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补．
【变式4-1】（2023春·八年级期末）如图，已知在△ABC中，∠A=40°，现将一块直角三角板放在△ABC上，使三角板的两条直角边分别经过点B,C，直角顶点D落在△ABC的内部，则∠ABD+∠ACD=（ ）．
A．90°B．60°C．50°D．40°
【答案】A
【分析】由三角形内角和定理可得∠ABC+∠ACB+∠A=180°，即∠ABC+∠ACB=180-∠A=140°，再说明∠DBC+∠DCB=90°，进而完成解答．
【详解】解：∵在△ABC中，∠A=40°
∴∠ABC+∠ACB=180-∠A=140°
∵在△DBC中，∠BDC=90°
∴∠DBC+∠DCB=180°-90°=90°
∴∠ABD+∠ACD=40°-90°=50°
故选C．
【点睛】本题主要考查三角形内角和定理，灵活运用三角形内角和定理成为解答本题的关键．
【变式4-2】（2023·全国·八年级假期作业）如图所示，已知四边形ABDC，求证∠BDC=∠A+∠B+∠C．
【答案】见解析
【分析】方法1连接BC，根据三角形内角和定理可得结果；
方法2 作射线AD，根据三角形的外角性质得到∠3=∠B+∠1，∠4=∠C+∠2，两式相加即可得到结论；
方法3延长BD，交AC于点E，两次运用三角形外角的性质即可得出结论．
【详解】方法1如图所示，连接BC.
在△ABC中，∠A+∠ABC+∠ACB=180∘，即∠A+∠ABD+∠1+∠ACD+∠2=180∘.
在△BCD中，∵∠BDC+∠1+∠2=180∘，
∴∠BDC=∠A+∠ABD+∠ACD；
方法2如图所示，连接AD并延长.
∵∠3是△ABD的外角，
∴∠3=∠1+∠ABD.
同理，∠4=∠2+∠ACD.
∴∠3+∠4=∠1+∠2+∠ABD+∠ACD.
即∠BDC=∠A+∠ABD+∠ACD.
方法3如图所示，延长BD，交AC于点E.
∵∠DEC是△ABE的外角，
∴∠DEC=∠A+∠ABD.
∵∠BDC是△DEC的外角，
∴∠BDC=∠DEC+∠ACD.
∴∠BDC=∠A+∠ABD+∠ACD.
【点睛】本题考查了三角形的外角性质：解题的关键是知道三角形的任一外角等于与之不相邻的两内角的和．也考查了三角形内角和定理．
【变式4-3】（2023春·福建南平·八年级统考期中）如图，若∠EOC=115°，则∠A+∠B+∠C+∠D+∠E+∠F= ．
【答案】230°
【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．
【详解】解：如图
∵∠EOC=∠E+∠2=115°，∠2=∠D+∠C，
∴∠E+∠D+∠C=115°，
∵∠EOC=∠1+∠F=115°，∠1=∠A+∠B，
∴∠A+∠B+∠F=115°，
∴∠A+∠B+∠C+∠D+∠E+∠F=230°，
故答案为：230°．
【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．
【知识点5 风筝模型】

【条件】四边形ABPC，分别延长AB、AC于点D、E，如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图，连接AP，则：∠PBD=∠PAB+∠APB，∠PCE=∠PAC+∠APC，
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC，得证.
【题型5 风筝模型】
【例5】（2023春·重庆渝北·八年级校考期中）如图,将△ABC沿着DE翻折,使B点与B'点重合,若∠1+∠2=80°,则∠B的度数为（ ）
A．20°B．30°C．40°D．50°
【答案】A
【分析】由折叠的性质可知∠BED=∠B'ED,∠BDE=∠B'DE,再利用平角的定义可求出∠BED+∠BDE的度数，进而利用三角形内角和可求∠B的度数.
【详解】由折叠的性质可知∠BED=∠B'ED,∠BDE=∠B'DE
∵∠1+∠BED+∠B'ED=180°,∠2+∠BDE+∠B'DE=180°
∴∠BED+∠BDE=12(360°−∠1−∠2)=12×(360°−80°)=140°
∴∠B=180°−(∠BED+∠BDE)=180°−140°=40°
故选C
【点睛】本题主要考查折叠的性质及三角形内角和定理，掌握折叠的性质及三角形内角和定理是解题的关键.
【变式5-1】（2023春·八年级期末）如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A＝55°，∠1＝95°，则∠2的度数为（ ）．
A．14°B．15°C．28°D．30°
【答案】B
【分析】根据三角形内角和定理和平角定义证得∠FEB＋∠EFC＝360°－125°＝235°，再根据折叠性质得出∠B′EF＋∠EFC′＝∠FEB＋∠EFC＝235°，进而求得∠1＋∠2=110°即可求解．
【详解】解：∵∠A＝55°，
∴∠AEF＋∠AFE＝180°－55°＝125°，
∴∠FEB＋∠EFC＝360°－125°＝235°，
由折叠可得：∠B′EF＋∠EFC′＝∠FEB＋∠EFC＝235°，
∴∠1＋∠2＝235°－125°＝110°，
∵∠1＝95°，
∴∠2＝110°－95°＝15°，
【点睛】本题考查折叠性质、三角形的内角和定理、平角定义，熟练掌握折叠性质是解答的关键．
【变式5-2】（2023春·八年级期末）如图，三角形纸片ABC中，∠A=65°,∠B=75°，将∠C沿DE翻折，使点C落在△ABC外的点C'处．若∠1=20°，则∠2的度数为 ．
【答案】100°
【分析】根据三角形内角和定理求出∠C，根据折叠的性质求出∠C'，根据三角形的外角的性质计算，得到答案．
【详解】解：∵∠A=65°，∠B=75°，
∴∠C=180°−65°−75°=40°，
由折叠的性质可知，∠C'=∠C=40°，
∴∠3=∠1+∠C'=60°，
∴∠2=∠C+∠3=100°，
故答案是：100°．
【点睛】本题考查的是三角形内角和定理、折叠的性质，掌握三角形内角和等于180°是解题的关键．
【变式5-3】（2023春·全国·八年级专题练习）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝120°，则∠1+∠2的度数为（ ）
A．90°B．100°C．110°D．120°
【答案】D
【分析】连接A'A，先求出∠BAC，再证明∠1+∠2=2∠BAC即可解决问题．
【详解】解：如图，连接AA'，
∵A'B平分∠ABC，A'C平分∠ACB，
∴∠A'BC=12∠ABC，∠A'CB=12∠ACB，
∵∠BA'C=120°，
∴∠A'BC+∠A'CB=180°-120°=60°，
∴∠ABC+∠ACB=120°，
∴∠BAC=180°-120°=60°，
∵沿DE折叠，
∴∠DAA'=∠DA'A，∠EAA'=∠EA'A，
∵∠1=∠DAA'+∠DA'A=2∠DAA'，∠2=∠EAA'+∠EA'A=2∠EAA'，
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°，
故选：D．
【点睛】本题考查了三角形内角和定理、角平分线定义、三角形外角的性质、折叠变换等知识，解题的关键是正确添加辅助线，灵活应用所学知识，属于中考常考题型．
【知识点6 两内角角平分线模型】
【条件】△ABC中，BI、CI分别是∠ABC和∠ACB的角平分线，且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线，∴∵CI是∠ACB平分线，∴
由A→B→I→C→A的飞镖模型可知：
∠I=∠A+∠2+∠3=∠A++=∠A+=.
【题型6 两内角角平分线模型】
【例6】（2023春·江苏苏州·八年级期中）直线MN与直线PQ垂直相交于点O，点A在直线PQ上运动，点B在直线MN上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出∠CED的度数．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及反向延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，则∠ABO的度数为____（直接写答案）
【答案】（1）不发生变化，∠AEB=135°；（2）不发生变化，∠CED=67.5°；（3）60°或45°
【分析】（1）根据直线MN与直线PQ垂直相交于O可知∠AOB=90°，再由AE、BE分别是∠BAO和∠ABO的角平分线得出∠BAE=12∠OAB，∠ABE=12∠ABO，由三角形内角和定理即可得出结论；
（2）延长AD、BC交于点F，根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°，进而得出∠OAB+∠OBA=90°，故∠PAB+∠MBA=270°，再由AD、BC分别是∠BAP和∠ABM的角平分线，可知∠BAD=12∠BAP，∠ABC=12∠ABM，由三角形内角和定理可知∠F=45°，再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°，进而得出结论；
（3）由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=12∠BAO，∠EOQ=12∠BOQ，进而得出∠E的度数，由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°，在△AEF中，由一个角是另一个角的3倍分四种情况进行分类讨论．
【详解】解：（1）∠AEB的大小不变，
∵直线MN与直线PQ垂直相交于O，
∴∠AOB=90°，
∴∠OAB+∠OBA=90°，
∵AE、BE分别是∠BAO和∠ABO角的平分线，
∴∠BAE=12∠OAB，∠ABE=12∠ABO，
∴∠BAE+∠ABE=12（∠OAB+∠ABO）=45°，
∴∠AEB=135°；
（2）∠CED的大小不变．
延长AD、BC交于点F．
∵直线MN与直线PQ垂直相交于O，
∴∠AOB=90°，
∴∠OAB+∠OBA=90°，
∴∠PAB+∠MBA=270°，
∵AD、BC分别是∠BAP和∠ABM的角平分线，
∴∠BAD=12∠BAP，∠ABC=12∠ABM，
∴∠BAD+∠ABC=12（∠PAB+∠ABM）=135°，
∴∠F=45°，
∴∠FDC+∠FCD=135°，
∴∠CDA+∠DCB=225°，
∵DE、CE分别是∠ADC和∠BCD的角平分线，
∴∠CDE+∠DCE=112.5°，
∴∠CED =67.5°；
（3）∵∠BAO与∠BOQ的角平分线相交于E，
∴∠EAO=12∠BAO，∠EOQ=12∠BOQ，
∴∠E=∠EOQ-∠EAO=12（∠BOQ-∠BAO）=12∠ABO，
∵AE、AF分别是∠BAO和∠OAG的角平分线，
∴∠EAF=90°．
在△AEF中，
∵有一个角是另一个角的3倍，故有：
①∠EAF=3∠E，∠E=30°，∠ABO=60°；
②∠EAF=3∠F，∠E=60°，∠ABO=120°（舍弃）；
③∠F=3∠E，∠E=22.5°，∠ABO=45°；
④∠E=3∠F，∠E=67.5°，∠ABO=135°（舍弃）．
∴∠ABO为60°或45°．
故答案为：60°或45°．
【点睛】本题考查的是平行线的判定和性质，三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
【变式6-1】（2023春·全国·八年级专题练习）如图，BE平分∠ABD，CF平分∠ACD，BE与CF交于点G，若∠BDC=140°，∠BGC=100°，则∠A=（ ）
A．80°B．75°C．60°D．45°
【答案】A
【分析】连接BC,先求解∠DBC+∠DCB, 再求解∠GBC+∠GCB, 可得∠GBD+∠GCD, 再利用角平分线的定义可得：∠ABD+∠ACD, 从而可得：∠ABC+∠ACB, 再利用三角形的内角和定理可得∠A的大小.
【详解】解：连接BC, ∵∠BDC=140°,
∴∠DBC+∠DCB=180°−140°=40°,
∵∠BGC=100°,
∴∠GBC+∠GCB=180°−100°=80°,
∴∠GBD+∠GCD=∠GBC+∠GCB−∠DBC−∠DCB=40°,
∵ BE平分∠ABD，CF平分∠ACD，
∴∠ABD+∠ACD=2(∠GBD+∠GCD)=80°,
∴∠ABC+∠ACB=∠ABD+∠ACD+∠DBC+∠DCB=80°+40°=120°,
∴∠A=180°−(∠ABC+∠ACB)=60°.
故选：C.
【点睛】本题考查的是三角形的内角和定理的应用，角平分线的定义，熟练利用三角形的内角和定理求解与之相关的角的大小是解题的关键.
【变式6-2】（2023春·全国·八年级专题练习）如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，延长BO与∠ACB的外角平分线交于点D，若∠BOC＝130°，则∠D＝
【答案】40°
【分析】根据角平分线的定义结合三角形外角的性质即可得到结论．
【详解】解：∵∠ABC和∠ACB的角平分线交于点O，
∴∠ACO=12∠ACB，
∵CD平分∠ACE，
∴∠ACD=12∠ACE，
∵∠ACB+∠ACE=180°，
∴∠OCD=∠ACO+∠ACD=12（∠ACB+∠ACE）=12×180°=90°，
∵∠BOC＝130°，
∴∠D=∠BOC-∠OCD=130°-90°=40°，
故答案为：40°．
【点睛】本题考查了三角形的外角性质，角平分线的定义，熟练掌握相关性质和概念正确推理计算是解题的关键．
【变式6-3】（2023春·黑龙江哈尔滨·八年级校联考期末）如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．
（1）若∠MON=60°，则∠ACG= ；（直接写出答案）
（2）若∠MON=n°，求出∠ACG的度数；（用含n的代数式表示）
（3）如图2，若∠MON=80°，过点C作CF∥OA交AB于点F，求∠BGO与∠ACF的数量关系．
【答案】（1）60°；（2）90°-12n°；（3）∠BGO-∠ACF=50°
【分析】（1）根据三角形内角和定理求出∠BAO+∠ABO，根据角平分线的定义、三角形的外角性质计算，得到答案；
（2）仿照（1）的解法解答；
（3）根据平行线的性质得到∠ACF=∠CAG，根据（2）的结论解答．
【详解】解：（1）∵∠MON=60°，
∴∠BAO+∠ABO=120°，
∵AC、BC分别是∠BAO和∠ABO的角平分线，
∴∠CBA=12∠ABO，∠CAB=12∠BAO，
∴∠CBA+∠CAB=12（∠ABO+∠BAO）=60°，
∴∠ACG=∠CBA+∠CAB=60°，
故答案为：60°；
（2）∵∠MON=n°，
∴∠BAO+∠ABO=180°-n°，
∵AC、BC分别是∠BAO和∠ABO的角平分线，
∴∠CBA=12∠ABO，∠CAB=12∠BAO，
∴∠CBA+∠CAB=12（∠ABO+∠BAO）=90°-12n°，
∴∠ACG=∠CBA+∠CAB=90°-12n°；
（3）∵CF∥OA，
∴∠ACF=∠CAG，
∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG，
由（2）得：∠ACG=90°-12×80°=50°．
∴∠BGO-∠ACF=50°．
【点睛】本题考查的是角平分线的定义、平行线的性质、三角形的外角性质，掌握两直线平行、内错角相等是解题的关键．
【知识点7 两外角角平分线模型】
【条件】△ABC中，BI、CI分别是△ABC的外角的角平分线，且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线，∴，∵CO是∠FCB平分线，∴
由△BCO中内角和定理可知：
∠O=180°-∠2-∠5=180°--=180°--===
【题型7 两外角角平分线模型】
【例7】（2023春·江苏·八年级专题练习）【问题背景】
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
【简单应用】
（2）如图2， AP、CP分别平分∠BAD． ∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；
【问题探究】
（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．
【拓展延伸】
（4） ①在图4中，若设∠C=α，∠B=β，∠CAP=13∠CAB，∠CDP=13∠CDB，试问∠P与∠C、∠B之间的数量关系为： （用α、β表示∠P）；
②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE， 猜想∠P与∠B、∠D的关系，直接写出结论．
【答案】（1）见解析；（2）36°；（3）26°，理由见解析；（4）①∠P=2α+β3②∠P=180°+∠B+∠D2
【分析】（1）根据三角形内角和定理即可证明；
（2）直接利用（1）中的结论两次，两式相加，然后根据角平分线的性质求解即可；
（3）由AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，推出∠1=∠2，∠3=∠4，推出∠PAD=180°﹣∠2，∠PCD=180°﹣∠3，由∠P+（180°﹣∠1）=∠D+（180°﹣∠3），∠P+∠1=∠B+∠4，推出2∠P=∠B+∠D，即可解决问题．
（4）①同法利用（1）种的结论列出方程即可解决问题．
②同法利用（1）种的结论列出方程即可解决问题．
【详解】（1）在△AEB中，∠A+∠B+∠AEB=180°．
在△CED中，∠C+∠D+∠CED=180°．
∵∠AEB=∠CED，
∴∠A+∠B=∠C+∠D；
（2）由（1）得：∠1+∠B=∠3+∠P，∠4+∠D=∠2+∠P，
∴∠1+∠B+∠4+∠D =∠3+∠P+∠2+∠P．
∵∠1=∠2，∠3=∠4，
∴2∠P=∠B+∠D=46°+26°=72°，
∴∠P=36°．
（3）∠P=26°，理由是：如图3：
∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，
∴∠1=∠2，∠3=∠4，
∴∠PAD=180°﹣∠2，∠PCD=180°﹣∠3．
∵∠PAB=∠1，∠P+∠PAB =∠B+∠4，
∴∠P+∠1=∠B+∠4．
∵∠P+（180°﹣∠2）=∠D+（180°﹣∠3），
∴2∠P=∠B+∠D，
∴∠P=12（∠B+∠D）=12×（36°+16°）=26°．
（4）①设∠CAP=m，∠CDP=n，则∠CAB=3m，，∠CDB=3n，
∴∠PAB=2m，∠PDB=2n．
∵∠C+∠CAP=∠P+∠PDC，∠P+∠PAB=∠B+∠PDB，
∵∠C=α，∠B=β，
∴α+m=∠P+n，∠P+2m=β+2n，
∴α－∠P = n－m，∠P－β=2n－2m=2（n－m），
∴2α+β=3∠P
∴∠P=2α+β3．
故答案为：∠P=2α+β3．
②设∠BAP=x，∠PCE=y，则∠PAO=x，∠PCB=y．
∵∠PAO+∠P=∠PCD+∠D，∠B+∠BAO=∠OCD+∠D，
∴x+∠P=180°－y+∠D，∠B+2x=180°－2y+∠D，
∴∠P=180°+∠B+∠D2．
故答案为：∠P=180°+∠B+∠D2．
【点睛】本题考查了三角形内角和，三角形的外角的性质、多边形的内角和等知识，解题的关键是学会用方程的思想思考几何问题，属于中考常考题型．
【变式7-1】（2023春·全国·八年级专题练习）如图，五边形ABCDE在∠BCD,∠EDC处的外角分别是∠FCD,∠GDC,CP,DP分别平分∠FCD和∠GDC且相交于点P．若∠A=160°,∠B=80°,∠E=90°，则∠CPD= ．
【答案】105°
【分析】根据多边形内角和公式求出五边形的内角和，根据题意求出∠BCD＋∠CDE的度数，从而求出∠PCD＋∠PDC的度数，运用三角形内角和定理即可求出∠CPD的度数．
【详解】解：∵∠A＝160°，∠B＝80°，∠E＝90°，
∴∠BCD＋∠CDE＝（5−2）×180°−160°−80°−90°＝210°，
∴∠PCD＋∠PDC＝12（180°×2−210°）＝75°，
在△CPD中，∠CPD＝180°−（∠PCD＋∠PDC）＝180°−75°＝105°，
故答案为：105°．
【点睛】本题主要考查多边形内角和公式，三角形内角和定理，以及外角的平分线，根据已知条件求出∠BCD＋∠CDE的度数是解题的关键．
【变式7-2】（2023春·全国·八年级专题练习）如图，点P是ΔABC的外角∠BCE和∠CBF的角平分线交点，延长BP交AC于G，请写出∠A和∠CPG的数量关系.
【答案】∠CPG=90°+12∠A
【分析】先根据三角形外角的性质及角平分线的性质即可用含∠A的式子表示出∠CBP和∠BCP的和，再利用三角形外角的性质即可得到∠A和∠CPG的数量关系.
【详解】解：∵∠ACB+∠ABC=180°−∠A,
∴∠ECB+∠FBC=180°×2−(180°−∠A)=180°+∠A,
∵点P是ΔABC的外角∠BCE和∠CBF的角平分线交点，
∴∠CBP+∠BCP＝12(180°+∠A)=90°+12∠A，
又∵∠CPG＝∠CBP+∠BCP，
∴∠CPG=90°+12∠A.
【点睛】本题考查了三角形内角和定理、三角形外角和的性质及角平分线的性质.熟练应用三角形外角的性质是解题的关键.
【变式7-3】（2023春·八年级期末）如图1，△ABC的外角平分线交于点F．
（1）若∠A＝40°，则∠F的度数为 ；
（2）如图2，过点F作直线MN∥BC，交AB，AC延长线于点M，N，若设∠MFB＝α，∠NFC＝β，则∠A与α+β的数量关系是 ；
（3）在（2）的条件下，将直线MN绕点F转动．
①如图3，当直线MN与线段BC没有交点时，试探索∠A与α，β之间的数量关系，并说明理由；
②当直线MN与线段BC有交点时，试问①中∠A与α，β之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请给出三者之间的数量关系．
【答案】（1）70°（2）α+β−12∠A=90° （3）①见解析 ②不成立；β−α−12∠A=90°或α−β−12∠A=90°
【分析】（1）根据三角形内角和定理以及角平分线的定义，即可得到∠F的度数；
（2）根据三角形内角和定理以及角平分线的定义，即可得到∠BFC的度数，再根据平行线的性质，即可得到∠A与α+β的数量关系；
（3）①根据（2）中的结论∠BFC＝90°﹣12∠A，以及平角的定义，即可得到∠A与α，β之间的数量关系；
②分两种情况进行讨论，根据（2）中的结论∠BFC＝90°﹣12∠A，以及平角的定义，即可得到∠A与α，β之间的数量关系．
【详解】解：（1）如图1，∵∠A＝40°，
∴∠ABC+∠ACB＝140°，
∴∠DBC+∠ECB＝360°﹣140°＝220°，
又∵△ABC的外角平分线交于点F，
∴∠FBC+∠FCB＝12（∠DBC+∠ECB）＝12×220°＝110°，
∴△BCF中，∠F＝180°﹣110°＝70°，
故答案为：70°；
（2）如图2，∵∠ABC+∠ACB＝180°﹣∠A，
∴∠DBC+∠ECB＝360°﹣（180°﹣∠A）＝180°+∠A，
又∵△ABC的外角平分线交于点F，
∴∠FBC+∠FCB＝12（∠DBC+∠ECB）＝12×（180°+∠A）＝90°+12∠A ，
∴△BCF中，∠BFC＝180°﹣（90°+12∠A ）＝90°﹣12∠A，
又∵∠MFB＝α，∠NFC＝β，MN∥BC，
∴∠FBC＝α，∠FCB＝β，
∵△BCF中，∠FBC+∠FCB+∠BFC＝180°，
∴α+β+90°﹣12∠A＝180°，
即α+β﹣12∠A＝90°，
故答案为：α+β﹣12∠A＝90°；
（3）①α+β﹣12∠A＝90°，理由如下：
如图3，由（2）可得，∠BFC＝90°﹣12∠A，
∵∠MFB+∠NFC+∠BFC＝180°，
∴α+β+90°﹣12∠A＝180°，
即α+β﹣12∠A＝90°，
②当直线MN与线段BC有交点时，①中∠A与α，β之间的数量关系不成立．
分两种情况：
如图4，当M在线段AB上，N在AC延长线上时，
由（2）可得，∠BFC＝90°﹣12∠A，
∵∠BFC﹣∠MFB+∠NFC＝180°，
∴90°﹣12∠A﹣α+β＝180°，
即β﹣α﹣12∠A＝90°；
如图5，当M在AB的延长线上，N在线段AC上时，
由（2）可得，∠BFC＝90°﹣12∠A，
∵∠BFC﹣∠NFC+∠MFB＝180°，
∴90°﹣12∠A﹣β+α＝180°，
即α﹣β﹣12∠A＝90°；
综上所述，∠A与α，β之间的数量关系为β﹣α﹣12∠A＝90°或α﹣β﹣12∠A＝90°．
【点睛】此题主要考查三角形的角度求解与证明，解题的关键是根据题意分情况作图．
【知识点8 内外角角平分线模型】
【条件】△ABC中，BP、CP分别是△ABC的内角和外角的角平分线，且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线，∴ ∵CP是∠ACE平分线，∴
由△ABC外角定理可知：∠ACE=∠ABC+∠A即：2∠1=2∠3+∠A ……①
对①式两边同时除以2，得：∠1=∠3+ ……②又在△BPC中由外角定理可知：∠1=∠3+∠P ……③
比较②③式子可知：.==.
【题型8 内外角角平分线模型】
【例8】（2023春·八年级期末）如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD的平分线，CA3是∠A2CD的平分线，……以此类推，若∠A=α，则∠A2020= ．
【答案】α22020
【分析】根据角平分线的定义可得∠A1BC=12∠ABC，∠A1CD=12∠ACD，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC，∠A1CD=∠A1BC+∠A1，整理即可得解∠A1=12∠A，同理求出∠A2，∠A3，可以发现后一个角等于前一个角的12，根据此规律即可得解．
【详解】∵A1B是∠ABC的平分线，A1C是∠ACD的平分线，
∴∠A1BC=12∠ABC，∠A1CD=12∠ACD，
又∵∠ACD=∠A+∠ABC，∠A1CD=∠A1BC+∠A1，
∴12（∠A+∠ABC）=12∠ABC+∠A1，
∴∠A1=12∠A，
∵∠A=α．
∠A1=12∠A=12α，同理可得∠A2=12∠A1=122α，
根据规律推导，
∴∠A2020= α22020，
故答案为α22020．
【点睛】本题主要考查的是三角形外角性质，角平分线定理，熟知三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义是解题的关键．
【变式8-1】（2023春·八年级期末）如图，已知△ABC的两条高BD、CE交于点F，∠ABC的平分线与△ABC外角∠ACM的平分线交于点G，若∠BFC=8∠G，则∠A= °．
【答案】36
【分析】首先根据三角形的外交性质求出∠A=2∠G，结合三角形的高的知识得到∠G和∠A之间的关系，进而可得结果；
【详解】由图知：∠ACM=∠A+∠ABC，
∵CG是∠ACM的角平分线，
∴∠ACM=2∠GCM，
∴∠A+∠ABC=2∠GCM，
∵BG是∠ABC的角平分线，
∴∠GBC=12∠ABC，
∴∠GBC+∠G=∠GCM，
即12∠ABC+∠G=∠GCM，
∴∠ABC+2∠G=2∠GCM，
∴∠ABC+2∠G=∠A+∠ABC，
∴∠A=2∠G，
∵△ABC的两条高BD、CE交于点F，
∴CE⊥AB，BD⊥AC，
∴∠AEF=∠ADF=90°，
∴在四边形AEFD中有：∠A+∠DFE=180°，
∵∠DFE=∠BFC，
∴∠A+∠BFC=180°，
∵∠BFC=8∠G=8×12∠A=4∠A，
∴∠A+∠BFC=∠A+4∠A=5∠A=180°，
∴∠A=180°÷5=36°．
故答案为：36．
【点睛】本题主要考查了与角平分线有关的三角形的内角和与外角性质，准确分析计算是解题的关键．
【变式8-2】（2023春·八年级期末）如图，在△ABC中，∠A=60°，BD、CD分别平分∠ABC、∠ACB，M、N、Q分别在DB、DC、BC的延长线上，BE、CE分别平分∠MBC、∠BCN，BF、CF分别平分∠EBC、∠ECQ，则∠F= ．
【答案】15°
【分析】先由BD、CD分别平分∠ABC、∠ACB得到∠DBC=12∠ABC，∠DCB=12∠ACB，在△ABC中根据三角形内角和定理得∠DBC+∠DCB=12（∠ABC+∠ACB）=12（180°-∠A）=60°，则根据平角定理得到∠MBC+∠NCB=300°；再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6=12∠MBC，∠1=12∠NCB，两式相加得到∠5+∠6+∠1=12（∠NCB+∠NCB）=150°，在△BCE中，根据三角形内角和定理可计算出∠E=30°；再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6，∠2=∠3+∠4，根据三角形外角性质得到∠3+∠4=∠5+∠F，∠2+∠3+∠4=∠5+∠6+∠E，利用等量代换得到∠2=∠5+∠F，2∠2=2∠5+∠E，再进行等量代换可得到∠F=12∠E．
【详解】解：如图：
∵BD、CD分别平分∠ABC、∠ACB，∠A=60°，
∴∠DBC=12∠ABC，∠DCB=12∠ACB，
∴∠DBC+∠DCB=12（∠ABC+∠ACB）=12（180°-∠A）=12×（180°-60°）=60°，
∴∠MBC+∠NCB=360°-60°=300°，
∵BE、CE分别平分∠MBC、∠BCN，
∴∠5+∠6=12∠MBC，∠1=12∠NCB，
∴∠5+∠6+∠1=12（∠NCB+∠NCB）=150°，
∴∠E=180°-（∠5+∠6+∠1）=180°-150°=30°，
∵BF、CF分别平分∠EBC、∠ECQ，
∴∠5=∠6，∠2=∠3+∠4，
∵∠3+∠4=∠5+∠F，∠2+∠3+∠4=∠5+∠6+∠E，
即∠2=∠5+∠F，2∠2=2∠5+∠E，
∴2∠F=∠E，
∴∠F=12∠E=12×30°=15°．
故答案为：15°．
【点睛】本题考查了三角形内角和定理、角平分线、三角形外角性质，解题的关键是掌握三角形内角和是180°．
【变式8-3】（2023春·江苏南通·八年级南通田家炳中学校考期末）在△ABC中，若存在一个内角角度是另外一个内角角度的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝75°，∠C＝25°，可知∠B＝3∠C，所以△ABC为3倍角三角形．
（1）在△ABC中，∠A＝80°，∠B＝60°，则△ABC为 倍角三角形；
（2）若锐角三角形MNP是3倍角三角形，且最小内角为α，请直接写出α的取值范围为 ．
（3）如图，直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，若△AEF为4倍角三角形，求∠ABO的度数．
【答案】（1）2；（2）22.5°＜α＜30°；（3）45°或36°
【分析】（1）由∠A＝80°，∠B＝60°，可求∠C的度数，发现内角之间的倍数关系，得出答案，
（2）△DEF是3倍角三角形，必定有一个内角是另一个内角的3倍，然后根据这两个角之间的关系，分情况进行解答，
（3）首先证明∠EAF＝90°，分两种情形分别求出即可．
【详解】解：（1）∵∠A＝80°，∠B＝60°，
∴∠C＝180°﹣∠A﹣∠B＝40°，
∴∠A＝2∠C，
∴△ABC为2倍角三角形，
故答案为：2；
（2）∵最小内角为α，
∴3倍角为3α，
由题意可得：
3α＜90°，且180°﹣4α＜90°，
∴最小内角的取值范围是22.5°＜α＜30°．
故答案为22.5°＜α＜30°．
（3）∵AE平分∠BAO，AF平分∠AOG，
∴∠EAB＝∠EAO，∠OAF＝∠FAG，
∴∠EAF＝∠EAO+∠OAF＝12（∠BAO+∠OAG）＝90°，
∵△EAF是4倍角三角形，
∴∠E＝14×90°或15×90°，
∵AE平分∠BAO，OE平分∠BOQ，
∴∠E＝12∠ABO，
∴∠ABO＝2∠E，
∴∠ABO＝45°或36°．