银川市第二十四中学南校区2024届九年级下学期期中考试数学试卷(含解析)

这是一份银川市第二十四中学南校区2024届九年级下学期期中考试数学试卷(含解析)，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．手机信号的强弱通常采用负数来表示，绝对值越小表示信号越强（单位：），则下列信号最强的是（ ）
A．B．C．D．
2．下列运算正确的是（ ）
A．B．C．D．
3．河湟剪纸被列入青海省第三批省级非物质文化遗产名录，是青海劳动人民结合河湟文化，创造出独具高原特色的剪纸．以下剪纸图案既是轴对称图形又是中心对称图形的是（ ）
A． B． C． D．
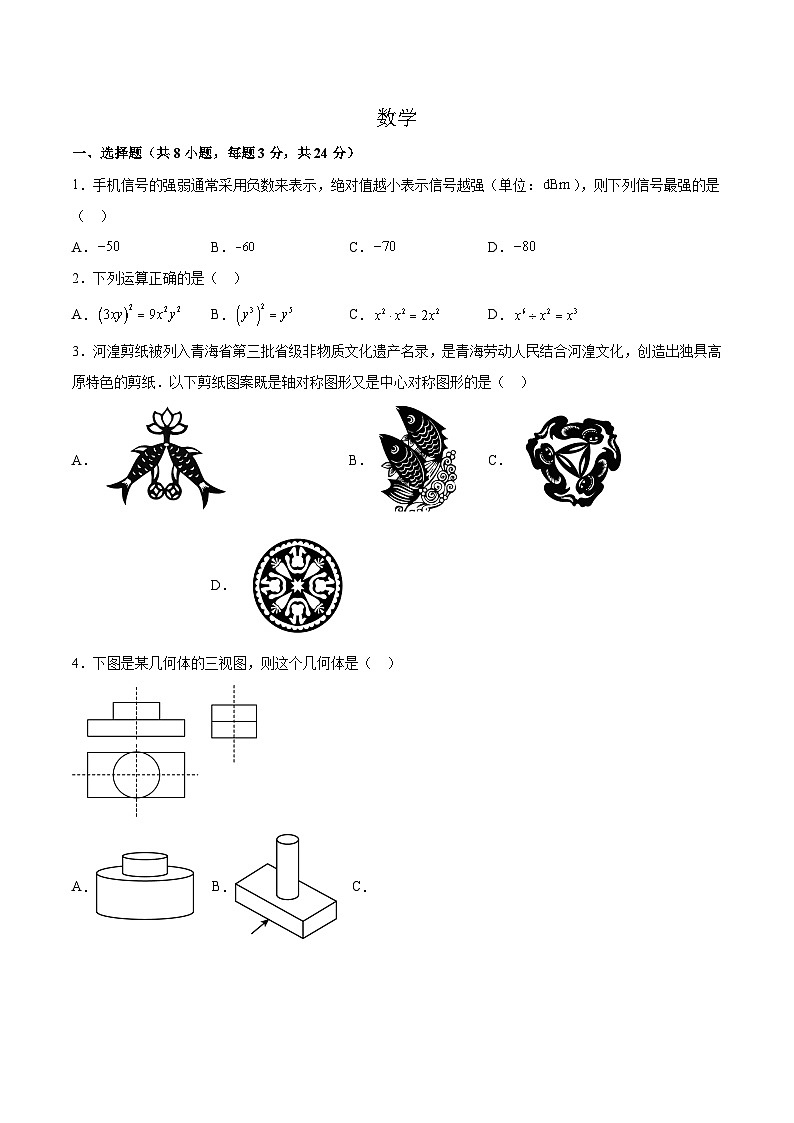
4．下图是某几何体的三视图，则这个几何体是（ ）

A． B． C．
D．
5．一副直角三角板如图放置，其中，，，点F在CB的延长线上若，则等于（ ）
A．35°B．25°C．30°D．15°
6．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示．
这些运动员成绩的众数和中位数分别为（ ）
A．米，米B．米，米
C．米，米D．米，米
7．我国南宋数学家杨辉在1275年提出的一个问题：“直田积八百六十四步，只云阔不及长一十二步．问阔及长各几步．”意思是：长方形的面积是864平方步，宽比长少12步，问宽和长各是几步．设宽为x步，根据题意列方程正确的是（ ）
A．B．
C．D．
8．伟大的古希腊哲学家、数学家、物理学家阿基米德有句名言：“给我一个支点，我可以撬动地球！”这句名言道出了“杠杆原理”的意义和价值．“杠杆原理”在实际生产和生活中，有着广泛的运用．比如：小明用撬棍撬动一块大石头，运用的就是“杠杆原理”．已知阻力和阻力臂的函数图象如图，若小明想使动力不超过，则动力臂（单位：需满足（ ）
A． B．C．D．
二、填空题（共8小题，每题3分，共24分）
9．一颗中高轨道卫星距离地面高度大约是米，将数据用科学记数法表示为 ．
10．分解因式： ．
11．有五张看上去无差别的卡片，正面分别写着，，，，0．背面朝上混合后随机抽取一张，取出的卡片正面的数字是无理数的概率是 ．
12．已知二次函数的图象与x轴有两个交点，则k的取值范围是 ．
13．如图，在边长为1的小正方形组成的网格中，A，B，C，D四个点均在格点上，与相交于点E，连接，则与的周长比为 ．
14．如图，在直径为的中，点C，D在圆上，，若，则的度数为 ．
15．如图，在矩形中，对角线与相交于点O，，，垂足为点E，F是的中点，连接，若，则矩形的周长是 ．
16．如图，在直角中，，，将绕点顺时针旋转至的位置，点是的中点，且点在反比例函数的图象上，则的值为 ．

三、解答题（共72分）
17．先化简，再求值：，其中．
18．如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（4，1），B（2，3），C（1，2）．

(1)画出与△ABC关于y轴对称的△A1B1C1；
(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为，并写出点B2的坐标．
19．某校举行“二十大知识学习竞赛”活动，老师让班长小华到商店购买笔记本作为奖品，商店每本硬面笔记本比软面笔记本贵3元（单价均为整数）．小华发现用240元购买硬面笔记本与用195元购买软面笔记本的数量相同。
(1)分别求出硬面笔记本和软面笔记本的单价．
(2)小华打算购买两种类型笔记本共50本，且购买的软面笔记本的数量不超过硬面笔记本的2倍，则小华的最低费用是多少？
20．为落实“双减”政策，某校随机调查了50名学生平均每天完成书面作业所需时间的情况，根据调查数据绘制了如下不完整的统计图、表：
(1)分别写出a、b的值并补全条形统计图；
(2)若该校有学生1000人，估计每天完成书面作业的时间不足小时的学生约有多少人?
(3)学校需要深入了解影响作业时间的因素，现从E组的4人中随机抽取2人进行谈话，已知E组中七、八年级各1人，九年级2人，则抽取的2人都是九年级学生的概率为多少?
21．如图，在四边形ABCD中，AC与BD相交于点O，且，点E在BD上，．
(1)求证：四边形AECD是平行四边形；
(2)若，，，，求BE的长．
22．如图，反比例函数与一次函数的图象交于点，轴于点D，分别交反比例函数与一次函数的图象于点B，C．
(1)求反比例函数与一次函数的表达式；
(2)当时，求的面积．
23．如图，中，，为斜边中线，以为直径作交于点，过点作，垂足为点．
(1)求证：为的切线；
(2)若直径，，求的长．
24．为增强民众生活幸福感，某社区服务队在休闲活动场所的墙上安装遮阳棚，方便居民使用．如图，在侧截面示意图中，遮阳棚长4米，与水平线的夹角为，且靠墙端离地的高为4米，当太阳光线与地面的夹角为时，求的长．（结果精确到0.1米；参考数据：，，，，，）
25．如图，在平面直角坐标系中，直线l与x轴交于点，与y轴交于点，抛物线经过点A，B，且对称轴是直线．
(1)求抛物线的解析式；
(2)在y轴上找一点Q（不与点O重合），使为等腰三角形，请直接写出点Q的坐标；
(3)点P是直线l下方抛物线上的一动点，过点P作轴，垂足为C，交直线l于点D，过点P作，垂足为M．求的最大值及此时P点的坐标．
26．综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆，车轮都是圆形的.为什么车轮要做成圆形的呢？这里面有什么数学道理吗？带着这样的疑问，小青做了如下的探究活动：
将车轮设计成不同的正多边形，在水平地面上模拟行驶.

(1)探究一：将车轮设计成等边三角形，转动过程如图1，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，，圆心角.此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是（水平线），请在图2中计算C到的距离.
(2)探究二：将车轮设计成正方形，转动过程如图3，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，，圆心角.此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是（水平线），请在图4中计算C到的距离（结果保留根号）.
(3)探究三：将车轮设计成正六边形，转动过程如图5，设其中心到顶点的距离是2，以车轮转动一次（以一个顶点为支点旋转）为例，中心的轨迹是，圆心角______.此时中心轨迹最高点是C（即的中点），转动一次前后中心的连线是（水平线），在图6中计算C到的距离______（结果保留根号）.
(4)归纳推理：比较，，大小：______，按此规律推理，车轮设计成的正多边形边数越多，其中心轨迹最高点与转动一次前后中心连线（水平线）的距离______（填“越大”或“越小”）.
(5)得出结论：将车轮设计成圆形，转动过程如图7，其中心（即圆心）的轨迹与水平地面平行，此时中心轨迹最高点与转动前后中心连线（水平线）的距离______.这样车辆行驶平稳、没有颠簸感.所以，将车轮设计成圆形.
参考答案与解析
1．A
详解：解：，
则信号最强的是，
故选：A．
2．A
详解：解：A．，故此选项符合题意；
B．，故此选项不合题意；
C．，故此选项不合题意；
D．，故此选项不合题意．
故选：A．
3．D
详解：解：A．是轴对称图形，不是中心对称图形，故该选项不符合题意；
B．既不是轴对称图形，也不是中心对称图形，故该选项不符合题意；
C．既不是轴对称图形，也不是中心对称图形，故该选项不符合题意；
D．既是轴对称图形，又是中心对称图形，故该选项符合题意．
故选D．
4．C
详解：解：结合三视图发现：该几何体为圆柱和长方体的结合体，
故选：C．
5．D
详解：解：由题意可得：∠EDF=30°，∠ABC=45°，
∵DE∥CB，
∴∠BDE=∠ABC=45°，
∴∠BDF=45°-30°=15°．
故选：D．
6．A
详解：解：观察表中可知，出现了5次，次数最多，
运动员的成绩的众数为：米．
将表中的数据按照从小到大的顺序排列如下：
，，，，，，，，，，，，，，
运动员的成绩的中位数是米．
故选：A．
7．D
详解：解：设宽为x步，则长为步，
由题意得：，
故选：D．
8．D
详解：解：阻力和阻力臂的函数关系式为，
点在该函数图象上，
，
解得，
阻力和阻力臂的函数关系式为，
，
，
当时，，
小明想使动力不超过，则动力臂（单位：需满足，
故选：D．
9．
详解：解：
故答案为：．
10．
详解：解：原式
．
故答案为：．
11．
详解：解：在，，，，0中，
无理数有，，共2个，
∴随机抽取一张，取出的卡片正面的数字是无理数的概率是，
故答案为：．
12．且
详解：解：由题意，二次函数的图象与轴有两个交点，
，且．
且．
且．
故答案为：且．
13．##2
详解：如图：由题意可知，，，
∴，
而，
∴四边形为平行四边形，
∴，
∴，，
∴，
∴．
故答案为：．
14．##34度
详解：解：∵，，
∴，
∴，
∵四边形是的内接四边形，
∴，
∴，
∵是的直径，
∴，
∴．
故答案为：．
15．##
详解：解：∵四边形是矩形，
∴，
∵，
∴为等边三角形，
∵，
∴点E为中点，
∵F是的中点，若，
∴，
∵，
∴，
∴，
∴矩形的周长，
故答案为：．
16．
详解：解：如图，作轴，垂足为．

由题意，在中，，，
．
．
．
又绕点顺时针旋转至的位置，
．
．
又点是的中点，
．
在中，
，
．
，．
又在上，
．
故答案为：．
17．，原式
详解：解：原式
，
当时，原式．
18．(1)作图见解析
(2)作图见解析
详解：（1）如图，为所作．
（2）如图，为所作，点B2的坐标为（-4，-6）．
19．(1)硬面笔记本的单价为16元，软面笔记本的单价为13元；
(2)小华的最低费用是701元．
详解：（1）解：设硬面笔记本的单价为元，则软面笔记本的单价为元，
根据题意得：，
解得：，
经检验，是所列方程的解，且符合题意，
，
答：硬面笔记本的单价为16元，软面笔记本的单价为13元；
（2）解：设购买硬面笔记本本，则购买软面笔记本本，
由题意得：，
解得：，
为正整数，
的最小值为17，
设购买两种类型笔记本的费用为元，
由题意得：，
，
随的增大而增大，
当时，有最小值，
答：小华的最低费用是701元．
20．(1)，，图见解析
(2)人
(3)
详解：（1）解：由图形知，
则，
补全图形如下：
（2）解：(人)，
答：估计每天完成书面作业的时间不足1.5小时的学生约有820人；
（3）解：将七、八、九年级的学生分别记作七1、八1、九1、九2，画树形图如图所示：
共有12种等可能情况，其中抽取的两名学生都来自九年级的有2种情况，
∴抽取的两名学生都来自九年级的概率为．
21．(1)证明见解析
(2)3
详解：（1）证明：∵，
∴，
在和中，
∵，
∴，
∴，
∴四边形AECD是平行四边形．
（2）解：∵，，
∴，
∵四边形AECD是平行四边形，
∴，，
∵，
∴，
在中，由勾股定理得，
∴，
∴，即，
解得，
∴，
∴的长为3．
22．(1)反比例函数的表达式为；一次函数的表达式为
(2)
详解：（1）解：∵反比例函数的图象经过点，
∴，
∴反比例函数的表达式为；
∵一次函数的图象经过点，
∴，
∴，
∴一次函数的表达式为；
（2）解：∵，
∴，
∴直线的表达式为，
∵时，，
解得，则，
∵时，，
解得，则，
∴，
，
．
23．(1)见解析
(2)
详解：（1）证明：连接，如下图所示：
以为直径作交于点，
，
，
在中，，为斜边中线，
，
，
，
∴，
，
，
又为半径，
为的切线；
（2）解：，，
，
，
在中，，
由勾股定理得：，
为直径，
，
又∵，
∴，
，
，，
，
又，
，
，
即，
．
24．的长为．
详解：解：过点作于点，作于点，
由题易知四边形为矩形，
，，
遮阳棚长4米，与水平线的夹角为，
，
，
高为4米，
，
，
又太阳光线与地面的夹角为，
，
．
25．(1)
(2)，或
(3)的最大值是，此时的P点坐标是
详解：（1）解：设抛物线的解析式为，
∵抛物线的对称轴为直线，
∴．
把A，B两点坐标代入解析式，得，
解得：，
∴抛物线的解析式为；
（2）解：∵ ，
∴，
∴，
∵为等腰三角形，点Q在y轴上（不与点O重合），
当时，
，
或；
当时，
，
，
；
综上所述，，或；
（3）解：∵在中，，
∴．
∵轴，，
∴．
在中，，，
∴，
∴．
在中，，，
∴，
∴．
设直线l的解析式为，
把A，B两点的坐标代入解析式，得，
解得：，
∴直线l的解析式为；
设点P的坐标为，则，
∴．
∵，
∴当时，有最大值是，此时最大，
∴，
当时，，
∴，
∴的最大值是，此时的P点坐标是．
26．(1)1
(2)
(3)
(4)，越小
(5)0
详解：（1）解：图1，
，，
，
，
是等边三角形，
，
∵C为的中点，为半径，
∴，
；
（2）解：如图2，
，，，
，
，
；
（3）解：如图3，
，，
是等边三角形，
，
在中，
，
，
故答案为：，；
（4）解：，
，则其中心轨迹最高点与转动一次前后中心连线（水平线）的距离越小；
故答案为：；越小．
（5）解：圆的半径相等，
，
故答案为：0．成绩/米
人数
2
3
5
4
1
分组
时间x（时）
人数
A
5
B
16
C
a
D
b
E
4