北师大版七年级数学下册举一反三系列7.4期中真题重组卷(考查范围：第1~3章)(北师大版)同步学案(学生版+解析)

这是一份北师大版七年级数学下册举一反三系列7.4期中真题重组卷(考查范围：第1~3章)(北师大版)同步学案(学生版+解析)，共27页。
【北师大版】
一．选择题（共10小题，满分30分，每小题3分）
1．(3分）（2022秋·四川宜宾·八年级统考期中）已知2x+3x−1=2x2+mx+n，则m−n的值是（ ）
A．−10B．10C．−2D．2
2．(3分）（2022春·湖南娄底·七年级统考期中）如果a2n−1an+5=a16，那么n的值为（ ）
A．4B．5C．6D．7
3．(3分）（2022秋·河南南阳·八年级统考期中）已知，a=255，b=344，c=433，则a、b、c的大小关系是（ ）
A．b>c>aB．a>b>cC．c>a>bD．c>b>a
4．(3分）（2022春·广东广州·七年级校考期中）如图所示，一只电子猫从A点出发，沿北偏东60°方向走了4m到达B点，再从B点向南偏西15°方向走了3m到达C点，那么∠ABC的度数为( )．
A．45°B．75°C．105°D．135°
5．(3分）（2022春·重庆·七年级重庆一中校考期中）如图，直线AB∥MN，点C为直线MN上一点，连接AC、BC，∠CAB＝40°，∠ACB＝90°，∠BAC的角平分线交MN于点D，点E是射线AD上的一个动点，连接CE、BE，∠CED的角平分线交MN于点F．当∠BEF＝70°时，令∠ECM=α，用含α的式子表示∠EBC为（ ）．
A．52αB．10°−αC．10°−12αD．12α−10°
6．(3分）（2022春·陕西宝鸡·七年级统考期中）某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据
下列说法错误的是（ ）A．这个问题中，空气温度和声速都是变量
B．空气温度每降低10℃，声速减少6m/s
C．当空气温度为20℃时，声音5s可以传播1710m
D．由数据可以推测，在一定范围内，空气温度越高，声速越快
7．(3分）（2022春·江西南昌·七年级江西师范大学附属外国语学校校考期中）如图，已知直线AB，CD被直线AC所截，AB∥CD．E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：①α−β，②α+β，③180°−α−β，④360°−α−β，∠AEC的度数可能是（ ）
A．①②③B．①②④C．①③④D．①②③④
8．(3分）（2022秋·湖南衡阳·八年级衡阳市实验中学校考期中）计算2+122+124+128+1⋯264+1，结果的个位数字是（ ）
A．6B．5C．8D．7
9．(3分）（2022春·全国·八年级期中）2013年“中国好声音”全国巡演重庆站在奥体中心举行，童童从家出发前往观看，先匀速步行至轻轨车站，等了一会儿，童童搭乘轻轨至奥体中心观看演出，演出结束后，童童搭乘邻居刘叔叔的车顺利回到家．其中x表示童童从家出发后所用的时间，y表示童童离家的距离．下面能反映y与x函数关系的大致图象是【 】
A．B．C．D．
10．(3分）（2022春·广东广州·七年级校联考期中）如图，AB∥CD，点E，P在直线AB上（P在E的右侧），点G在直线CD上，EF⊥FG，垂足为F，M为线段EF上的一动点，连接GP，GM，∠FGP与∠APG的角平分线交与点Q，且点Q在直线AB，CD之间的区域，下列结论：①∠AEF+∠CGF＝90°；②∠AEF+2∠PQG＝270°；③若∠MGF＝2∠CGF，则3∠AEF+∠MGC＝270°；④若∠MGF＝n∠CGF，则∠AEF+1n+1∠MGC＝90°．正确的个数是（ ）
A．4B．3C．2D．1
二．填空题（共6小题，满分18分，每小题3分）
11．(3分）（2022秋·吉林长春·八年级统考期末）计算：−252022×−522023=______．
12．(3分）（2022春·内蒙古包头·七年级统考期中）计算：若am=8，an=2，则a2m−3n的值是_____．
13．(3分）（2022春·福建宁德·七年级统考期末）已知变量y与x的部分对应值如表格所示，则y与x的关系式是________.
14．(3分）（2022秋·上海浦东新·七年级校考期中）已知2022−a2020−a=16，那么a−20212=______．
15．(3分）（2022秋·山东潍坊·八年级统考期末）如图，两平面镜OM，ON的夹角∠MON，若任何射到平面镜ON上的入射光线AB，经过平面镜ON，OM两次反射后，使得AB∥CD，则∠MON=_______°．
16．(3分）（2022春·云南昆明·七年级统考期末）《七彩云南》少数民族传统艺术表演，是七彩云南欢乐世界的王牌演艺节目，它荟萃云南人文之美，深受观众喜爱．在展演中，舞台上的灯光由灯带上位于点A和点C的两盏激光灯控制．如图，光线AB与灯带AC的夹角∠A=40°，当光线CB'与灯带AC的夹角∠ACB'=______时，CB'∥AB．
三．解答题（共7小题，满分52分）
17．(6分）（2022秋·辽宁抚顺·八年级统考期末）计算：
(1)2x23−x2⋅x4
(2)(x+2)(x−3)+x
(3)12m3−6m2+3m÷3m
(4)(x+2y)(x−2y)−(x+y)2
18．(6分）（2022春·河南郑州·七年级郑州外国语中学校考期末）如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3=180°，试说明：∠GDC=∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知），
∴∠ADB=∠EFB=90°（________），
∴AD∥EF（________）．
∴_______+∠2=180°（________）
∵∠2+∠3=180° （已知）．
∴∠1=∠3（________）．
∴AB∥______（________）
∴∠GDC=∠B（________）．
19．(8分）（2022春·辽宁辽阳·七年级统考期末）在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，如表是测得的弹簧的长度y与所挂物体的质量x的几组对应值：
(1)在这个表格中反映的是________和_________两个变量之间的关系：_________是自变量，_________是因变量；
(2)弹簧长度y(cm)与所挂物体质量x(kg)的关系式是_________；
(3)若弹簧的长度为27cm时，此时所挂重物的质量是多少kg？（在弹簧的允许范围内）
20．(8分）（2022秋·四川广安·八年级统考期末）已知 x≠1．观察下列等式：
1−x1+x=1−x2；
1−x1+x+x2=1−x3；
1−x1+x+x2+x3=1−x4；
……
(1)猜想：1−x1+x+x2+x3+⋯+xn−1=___________；
(2)证明你在（1）中的猜想；
(3)根据你的猜想计算：x−1x2023+x2022+x2021+⋯+x2+x+1．
21．(8分）（2022秋·河北保定·八年级统考期末）图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
(1)图2中的阴影部分的正方形的边长等于___________；面积等于___________．
(2)观察图2，请你写出下列三个代数式(a+b)2，(a−b)2，ab之间的等量关系为___________．
(3)运用你所得到的公式，计算：若m、n为实数，且mn=5，m−n=4，试求m+n的值．
22．(8分）（2022秋·辽宁铁岭·七年级统考期末）已知点О为直线AB上一点，将直角三角板MON的直角顶点放在点O上，并在∠MON内部作射线OC．
(1)如图l，三角板的一边OM与射线OA重合．
①∠AOC的余角是___________，补角是___________；
②若∠BOC=120°，则∠NOC的度数为___________；
(2)如图2，将三角板放置到如图位置，使OC恰好平分∠MOB，且∠BON=4∠NOC，求∠AOM的度数；
(3)若仍将三角板按照如图2的方式放置，仅满足OC平分∠MOB，试猜想∠AOM与∠NOC之间的数量关系为___________．
23．(8分）（2022秋·四川宜宾·七年级统考期末）几何模型在解题中有着重要作用，例如美味的“猪蹄模型”．
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
x
…
1
2
3
4
…
y
…
12
14
16
18
…
所挂物体质量xkg
0
1
2
3
4
弹簧长度ycm
16
18
20
22
24
2022-2023学年七年级数学下册期中真题重组卷
（考查范围：第1~3章）
【北师大版】
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．(3分）（2022秋·四川宜宾·八年级统考期中）已知2x+3x−1=2x2+mx+n，则m−n的值是（ ）
A．−10B．10C．−2D．2
【答案】B
【分析】根据多项式乘以多项式展开得出m，n的值，然后代入求解即可．
【详解】解：∵2x+3x−1=2x2+4x−6=2x2+mx+n
∴m=4，n=−6，
∴m−n=4−−6=10，
【点睛】本题主要考查多项式的乘法及求代数式的值，熟练掌握多项式乘法法则是解题关键．
2．(3分）（2022春·湖南娄底·七年级统考期中）如果a2n−1an+5=a16，那么n的值为（ ）
A．4B．5C．6D．7
【答案】D
【分析】利用同底数幂的乘方的法则对式子进行整理，即可得到关于n的方程，即可求解．
【详解】∵a2n-1an+5=a16，
∴a2n-1+n+5=a16，
即a3n+4=a16，
∴3n+4=16，
解得：n=4．
【点睛】本题主要考查同底数幂的乘法，解答的关键是熟记同底数幂的乘法的法则．
3．(3分）（2022秋·河南南阳·八年级统考期中）已知，a=255，b=344，c=433，则a、b、c的大小关系是（ ）
A．b>c>aB．a>b>cC．c>a>bD．c>b>a
【答案】D
【分析】首先根据幂的乘方运算的逆用可得，a=3211，b=8111，c=6411，再根据指数相等时，底数越大，幂就越大，据此即可解答．
【详解】解：a=255=（25）11=3211，b=344=（34）11=8111，c=433=（43）11=6411，
∵81>64>32，
∴8111>6411>3211，
∴b>c>a，
【点睛】本题考查了幂的乘方运算的逆用，有理数大小的比较，熟练掌握和运用幂的乘方运算的逆用是解决本题的关键．
4．(3分）（2022春·广东广州·七年级校考期中）如图所示，一只电子猫从A点出发，沿北偏东60°方向走了4m到达B点，再从B点向南偏西15°方向走了3m到达C点，那么∠ABC的度数为( )．
A．45°B．75°C．105°D．135°
【答案】D
【分析】根据AD//BF，判断出∠ABF=∠A=60°，再根据∠CBF=15°，求出∠ABC=60°−15°=45°．
【详解】解：如图：∵AD//BF，
∴∠ABF=∠A=60°，
∵∠CBF=15°，
∴∠ABC=60°−15°=45°，
故选A．
【点睛】本题主要考查了方向角、平行线的性质、角的加减等知识点，熟悉方向角的定义及角的加减是解答本题的关键．
5．(3分）（2022春·重庆·七年级重庆一中校考期中）如图，直线AB∥MN，点C为直线MN上一点，连接AC、BC，∠CAB＝40°，∠ACB＝90°，∠BAC的角平分线交MN于点D，点E是射线AD上的一个动点，连接CE、BE，∠CED的角平分线交MN于点F．当∠BEF＝70°时，令∠ECM=α，用含α的式子表示∠EBC为（ ）．
A．52αB．10°−αC．10°−12αD．12α−10°
【答案】D
【分析】先求出∠ABC，再延长CE，交AB于点G，结合平行线的性质表示出∠BCE，然后根据三角形内角和定理表示∠CED，再根据角平分线得定义表示出∠CEB，最后根据三角形内角和定理得出答案．
【详解】在△ABC中，∠CAB=40°，∠ACB=90°，
∴∠ABC=50°．
延长CE，交AB于点G，
∵MN∥BA，
∴∠EGB=α，∠ACM=∠BAC=40°，
∴∠ACE=α-40°，
∴∠BCE=90°-（α-40°）=130°-α．
∵∠CEA=180°-∠CAE-∠ACE，
∴∠CED=180°-∠CEA=∠CAE+∠ACE=20°+（α-40°）=α-20°．
∵EF平分∠CED，
∴∠CEF=12∠CED=12α−10°，
∴∠CEB=12α−10°+70°=12α+60°，
∴∠EBC=180°−(12α+60°)−(130°−α)=12α−10°．
故选：D．
【点睛】本题主要考查了角平分线的定义，三角形内角和定理，平行线的性质，将待求角转化到适合的三角形是解题的关键．
6．(3分）（2022春·陕西宝鸡·七年级统考期中）某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据
下列说法错误的是（ ）A．这个问题中，空气温度和声速都是变量
B．空气温度每降低10℃，声速减少6m/s
C．当空气温度为20℃时，声音5s可以传播1710m
D．由数据可以推测，在一定范围内，空气温度越高，声速越快
【答案】B
【分析】根据表格中两个变量的数据变化情况，逐项判断即可．
【详解】解：这个问题中，空气温度和声速都是变量，因此选项A不符合题意；
在一定的范围内，空气温度每降低10℃，声速减少6m/s，表格之外的数据就不一定有这样规律，因此选项B符合题意；
当空气温度为20℃时，声速为342m/s，声音5s可以传播342×5＝1710m，因此选项C不符合题意；
从表格可得，在一定范围内，空气温度越高，声速越快，因此选项D不符合题意；
【点睛】本题考查变量之间的关系，理解自变量、因变量之间的变化关系是正确判断的前提．
7．(3分）（2022春·江西南昌·七年级江西师范大学附属外国语学校校考期中）如图，已知直线AB，CD被直线AC所截，AB∥CD．E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：①α−β，②α+β，③180°−α−β，④360°−α−β，∠AEC的度数可能是（ ）
A．①②③B．①②④C．①③④D．①②③④
【答案】D
【分析】根据点E有6种可能位置，分情况进行讨论，依据平行线的性质进行计算求解即可．
【详解】解：如图1，过E作GH∥AB，则由AB//CD，可得GH∥CD
∴∠GEC＝∠DCE=β，∠GEA＝∠BAE=α，
∴∠AEC＝∠GEC−∠GEA=β−α．
如图2，同理可得∠AEC＝∠GEA−∠GEC=α−β．故①有可能，
如图3，同理可得∠AEC＝∠GEA+∠GEC=α+β．故②有可能，
其中：当∠AEC＝α+β=90°时，∠AEC＝180°−α−β=90°，故③有可能，
如图4，同理可得∠AEC＝360°−(∠GEA+∠GEC)=360°−α−β．故④有可能，
如图5，同理可得∠AEC＝∠GEC−∠GEA=β−α．
如图6，同理可得∠AEC＝∠GEA−∠GEC=α−β．
综上所述，①②③④均有可能．
故选：D．
【点睛】本题主要考查了平行线的性质和判定的运用，解题时注意：两直线平行，同位角相等；两直线平行，内错角相等．
8．(3分）（2022秋·湖南衡阳·八年级衡阳市实验中学校考期中）计算2+122+124+128+1⋯264+1，结果的个位数字是（ ）
A．6B．5C．8D．7
【答案】B
【分析】根据平方差公式将原式可化简为2128−1．求出2的乘方的前几项，总结出其个位数字依次为2，4，8，6，并依次循环出现．从而即得出2128的个位数字为6，进而得出2128−1的个位数字为5．
【详解】解：2+122+124+128+1⋯264+1
=22−122+124+128+1⋯264+1
=24−124+128+1⋯264+1
=28−128+1⋯264+1
…
=264−1264+1
=2128−1．
∵21=2，22=4，23=8，24=16，25=32，…，即其个位数字依次为2，4，8，6，并依次循环出现．
∵128÷4=32，
∴2128的个位数字为6，
∴2128−1的个位数字为6−1=5．
故选B．
【点睛】本题考查平方差公式的应用，数字类变化规律．正确利用平方差公式化简，并找出个位数字规律性的出现是解决问题的关键．
9．(3分）（2022春·全国·八年级期中）2013年“中国好声音”全国巡演重庆站在奥体中心举行，童童从家出发前往观看，先匀速步行至轻轨车站，等了一会儿，童童搭乘轻轨至奥体中心观看演出，演出结束后，童童搭乘邻居刘叔叔的车顺利回到家．其中x表示童童从家出发后所用的时间，y表示童童离家的距离．下面能反映y与x函数关系的大致图象是【 】
A．B．C．D．
【答案】D
【详解】童童先匀速步行至轻轨车站，图象平缓向上；
等了一会儿，图象平行于横轴；
搭乘轻轨至奥体中心，图象比步行陡一些向上；
观看演出，图象平行于横轴；
演出结束搭乘邻居刘叔叔的车回到家，图象向下．
综上所述，函数图象分为五段：平缓向上－平－陡些向上－平－向下．故选A．
10．(3分）（2022春·广东广州·七年级校联考期中）如图，AB∥CD，点E，P在直线AB上（P在E的右侧），点G在直线CD上，EF⊥FG，垂足为F，M为线段EF上的一动点，连接GP，GM，∠FGP与∠APG的角平分线交与点Q，且点Q在直线AB，CD之间的区域，下列结论：①∠AEF+∠CGF＝90°；②∠AEF+2∠PQG＝270°；③若∠MGF＝2∠CGF，则3∠AEF+∠MGC＝270°；④若∠MGF＝n∠CGF，则∠AEF+1n+1∠MGC＝90°．正确的个数是（ ）
A．4B．3C．2D．1
【答案】D
【分析】①过点F作FH∥AB，利用平行线的性质以及已知即可证明；
②利用角平分线的性质以及平行线的性质得到∠3=2∠2，∠CGF+2∠1+∠3=180°，结合①的结论即可证明；
③由已知得到∠MGC＝3∠CGF，结合①的结论即可证明；
④由已知得到∠MGC＝(n+1)∠CGF，结合①的结论即可证明．
【详解】解：①过点F作FH∥AB，如图：
∵AB∥CD，∴AB∥FH∥CD，
∴∠AEF=∠EFH，∠CGF=∠GFH，
∵EF⊥FG，即∠EFG=∠EFH+∠GFH=90°，
∴∠AEF+∠CGF=90°，故①正确；
②∵AB∥CD，PQ平分∠APG，GQ平分∠FGP，
∴∠APQ=∠2，∠FGQ=∠1，
∴∠3=∠APQ+∠2=2∠2，
∠CGF+∠FGQ+∠1+∠3=∠CGF+2∠1+∠3=180°，
即2∠1=180°-2∠2-∠CGF，
∴2∠2+2∠1=180°-∠CGF，
∵∠PQG=180°-(∠2+∠1)，
∴2∠PQG=360°-2(∠2+∠1)= 360°-(180°-∠CGF)= 180°+∠CGF，
∴∠AEF+2∠PQG=∠AEF+180°+∠CGF=180°+90°=270°，故②正确；
③∵∠MGF＝2∠CGF，
∴∠MGC＝3∠CGF，
∴3∠AEF+∠MGC＝3∠AEF+3∠CGF＝3(∠AEF+∠CGF)= 3×90°＝270°；
3∠AEF+∠MGC＝270°，故③正确；
④∵∠MGF＝n∠CGF，
∴∠MGC＝(n+1)∠CGF，即∠CGF=1n+1∠MGC，
∵∠AEF+∠CGF=90°，
∴∠AEF+1n+1∠MGC＝90°，故④正确．
综上，①②③④都正确，共4个，
【点睛】本题主要考查了平行线的性质，角平分线的定义等知识点，作辅助线求得∠AEF+∠CGF=90°，是解此题的关键．
二．填空题（共6小题，满分18分，每小题3分）
11．(3分）（2022秋·吉林长春·八年级统考期末）计算：−252022×−522023=______．
【答案】−52
【分析】根据同底数幂的乘法与积的乘方的法则，进行计算即可解答．
【详解】−252022×−522023
=(−25)2022×(−52)2022×−52
=(25×52)2022×−52
=12022×−52
=1×−52
=−52．
故答案为：−52．
【点睛】本题考查了同底数幂的乘法与积的乘方的逆运算，熟练掌握幂的乘方与积的乘方运算法则是解题的关键．
12．(3分）（2022春·内蒙古包头·七年级统考期中）计算：若am=8，an=2，则a2m−3n的值是_____．
【答案】8
【分析】先逆用同底数幂的除法公式将a2m−3n化为am2÷an3，再逆用幂的乘方化为am2÷an3再代入即可求解．
【详解】解：a2m−3n=a2m÷a3n=am2÷an3=82÷23=64÷8=8．
故答案为：8
【点睛】本题考查了同底数幂的除法和幂的乘方两个公式的逆用，熟知两个运算公式并正确逆用是解题关键．
13．(3分）（2022春·福建宁德·七年级统考期末）已知变量y与x的部分对应值如表格所示，则y与x的关系式是________.
【答案】y=2x+10
【分析】本题考查用关系式法表示变量之间的关系，用关系式表示的变量间关系经常是根据题目中的已知条件和两个变量之间的关系,利用公式、变化规律或者数量关系得到等式.
【详解】x每增加1，y增加2，易得当x=0时y=10，所以y=2x+10.
【点睛】在做此类题时，如果发现x增加1时，y增加的数值固定，那么y=kx+b，k就是这个固定的值，b为x=0时y对应的值.
14．(3分）（2022秋·上海浦东新·七年级校考期中）已知2022−a2020−a=16，那么a−20212=______．
【答案】17
【分析】对已知等式变形，然后利用平方差公式计算即可．
【详解】解：∵2022−a2020−a=16，
∴2021−a+12021−a−1=16，
∴2021−a2−1=16，
∴2021−a2=17，
∴a−20212=17，
故答案为：17．
【点睛】本题考查了平方差公式的应用，掌握a+ba−b=a2−b2是解题的关键．
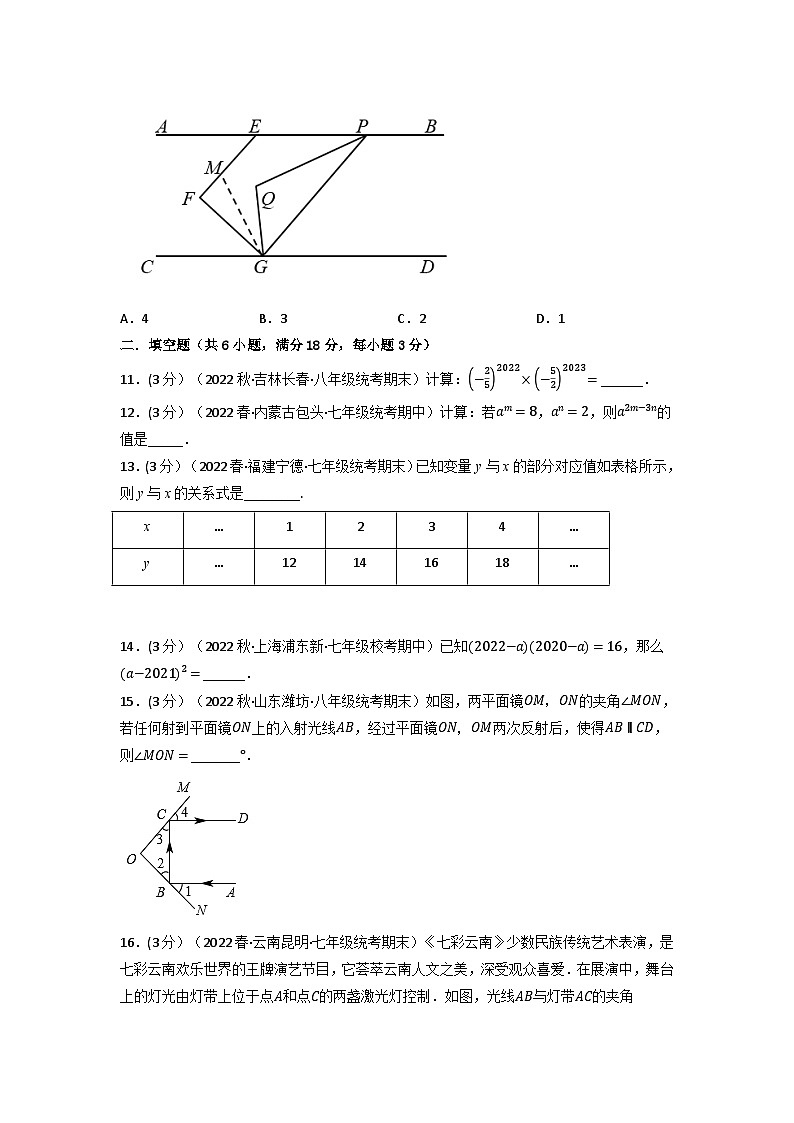
15．(3分）（2022秋·山东潍坊·八年级统考期末）如图，两平面镜OM，ON的夹角∠MON，若任何射到平面镜ON上的入射光线AB，经过平面镜ON，OM两次反射后，使得AB∥CD，则∠MON=_______°．
【答案】90
【分析】由平行线的性质得出∠DCB+∠ABC=180°，根据平角的定义得出∠1+∠2+∠ABC+∠3+∠4+∠DCB=180°+180°=360°，进而得到∠2+∠3=90°，再根据三角形的内角和即可得解．
【详解】解：∵AB∥CD，
∴∠DCB+∠ABC=180°，
∴∠1+∠2+∠ABC+∠3+∠4+∠DCB=180°+180°=360°，
∴∠1+∠2+∠3+∠4=180°，
∵∠1=∠2，∠3=∠4，
∴2∠2+∠3=180°，
∴∠2+∠3=90°，
∵∠MON+∠2+∠3=180°，
∴∠MON=180°−∠2−∠3=180°−90°=90°．
∴∠MON=90°，
故答案为：90．
【点睛】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．
16．(3分）（2022春·云南昆明·七年级统考期末）《七彩云南》少数民族传统艺术表演，是七彩云南欢乐世界的王牌演艺节目，它荟萃云南人文之美，深受观众喜爱．在展演中，舞台上的灯光由灯带上位于点A和点C的两盏激光灯控制．如图，光线AB与灯带AC的夹角∠A=40°，当光线CB'与灯带AC的夹角∠ACB'=______时，CB'∥AB．
【答案】140°或40°
【分析】当AB与CB'在AC同侧时，CB′∥AB，同旁内角互补；当AB与CB"在AC异侧时，CB"∥AB，内错角相等．
【详解】解：如下图：
当AB与CB′在AC同侧时，
当CB′∥AB时，
∵∠CAB+∠ACB′=180°
∴∠ACB′=140°
当AB与CB"在AC异侧时，
当CB"∥AB时，
∠CAB=∠ACB"=40°
答案：140°或40°．
【点睛】本题考查了平行线的性质，解题的关键是掌握两直线平行，内错角相等，同旁内角互补及需要由分论讨论的思想求解．
三．解答题（共7小题，满分52分）
17．(6分）（2022秋·辽宁抚顺·八年级统考期末）计算：
(1)2x23−x2⋅x4
(2)(x+2)(x−3)+x
(3)12m3−6m2+3m÷3m
(4)(x+2y)(x−2y)−(x+y)2
【答案】(1)7x6
(2)x2−6
(3)4m2−2m+1
(4)−5y2−2xy
【分析】（1）根据幂的乘方与同底数幂的乘法进行计算，然后合并同类项即可求解；
（2）根据多项式乘以多项式，然后合并同类项即可求解；
（3）根据多项式除以单项式进行计算即可求解；
（4）根据平方差公式与完全平方公式进行计算即可求解．
【详解】（1）解：2x23−x2⋅x4
=8x6−x6
=7x6；
（2）解：(x+2)(x−3)+x
=x2+2x−3x−6+x
=x2−6
（3）解：12m3−6m2+3m÷3m
=4m2−2m+1
（4）解：(x+2y)(x−2y)−(x+y)2
=x2−4y2−(x2+2xy+y2)
=x2−4y2−x2−2xy−y2
=−5y2−2xy．
【点睛】本题考查了幂的乘方与同底数幂的乘法，多项式乘以多项式，多项式除以单项式，平方差公式与完全平方公式，掌握以上运算法则以及乘法公式是解题的关键．
18．(6分）（2022春·河南郑州·七年级郑州外国语中学校考期末）如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3=180°，试说明：∠GDC=∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知），
∴∠ADB=∠EFB=90°（________），
∴AD∥EF（________）．
∴_______+∠2=180°（________）
∵∠2+∠3=180° （已知）．
∴∠1=∠3（________）．
∴AB∥______（________）
∴∠GDC=∠B（________）．
【答案】90；AD；EF；∠1；180；∠3；同角的补角相等；DG；内错角相等，两直线平行；两直线平行，同位角相等．
【分析】根据平行线的判定和性质，垂直的定义，同角的补角相等知识一一判断即可．
【详解】解：∵AD⊥BC，EF⊥BC （已知），
∴∠ADB=∠EFB=90°（垂直的定义），
∴AD∥EF（同位角相等，两直线平行）．
∴∠2+∠1=180°（两直线平行，同旁内角互补），
∵∠2+∠3=180°（已知）．
∴∠1=∠3（同角的补角相等）．
∴AB∥DG（内错角相等，两直线平行），
∴∠GDC=∠B（两直线平行，同位角相等）．
故答案为：90；AD；EF；∠1；180；∠3；同角的补角相等；DG；内错角相等，两直线平行；两直线平行，同位角相等．
【点睛】本题考查平行线的判定和性质，解题的关键是熟练掌握基本知识．
19．(8分）（2022春·辽宁辽阳·七年级统考期末）在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，如表是测得的弹簧的长度y与所挂物体的质量x的几组对应值：
(1)在这个表格中反映的是________和_________两个变量之间的关系：_________是自变量，_________是因变量；
(2)弹簧长度y(cm)与所挂物体质量x(kg)的关系式是_________；
(3)若弹簧的长度为27cm时，此时所挂重物的质量是多少kg？（在弹簧的允许范围内）
【答案】(1)所挂物体质量，弹簧长度；所挂物体质量；弹簧长度；
(2)y=2x+16
(3)5.5kg
【分析】（1）根据表格标注的内容解答即可；
（2）由表格可知，物体每增加1千克，弹簧长度增加2cm，据此即可写出弹簧长度y(cm)与所挂物体质量x(kg)的关系式；
（3）把y=27代入（2）中关系式计算即可．
【详解】（1）解：上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；
故答案为：所挂物体质量，弹簧长度；所挂物体质量；弹簧长度；
（2）解：∵物体每增加1千克，弹簧长度增加2cm，
∴y=2x+16；
（3）解：把y=27代入y=2x+16，
得2x+16=27，
解得：x=5.5．
因此，此时所挂重物的质量是5.5kg．
【点睛】本题考查了自变量与因变量的意义，以及用函数关系式表示变量间的关系，根据题意正确写出函数关系式是解题的关键．
20．(8分）（2022秋·四川广安·八年级统考期末）已知 x≠1．观察下列等式：
1−x1+x=1−x2；
1−x1+x+x2=1−x3；
1−x1+x+x2+x3=1−x4；
……
(1)猜想：1−x1+x+x2+x3+⋯+xn−1=___________；
(2)证明你在（1）中的猜想；
(3)根据你的猜想计算：x−1x2023+x2022+x2021+⋯+x2+x+1．
【答案】(1)1−xn
(2)见解析
(3)x2024−1
【分析】（1）根据所给的三个等式归纳规律解答即可；
（2）利用多项式乘多项式法则进行求解即可；
（3）利用（1）中的结论进行求解即可．
【详解】（1）∵1−x1+x=1−x2；
1−x1+x+x2=1−x3；
1−x1+x+x2+x3=1−x4；
……
∴1−x1+x+x2+x3+⋯+xn−1=1−xn，
故答案为：1−xn；
（2）证明：1−x1+x+x2+x3+⋯+xn−1
=1+x+x2+x3+⋯+xn−1−x+x2+x3+⋯+xn−1+xn
=1+x−x+x2−x2+x3−x3+⋯+xn−1−xn−1−xn
=1−xn；
（3）解：x−1x2023+x2022+x2021+⋯+x2+x+1
=−1−x1+x+x2+⋯+x2023
=−(1−x2024)
=x2024−1．
【点睛】本题主要考查多项式乘多项式，数字的变化规律，解答的关键是对应的运算法则的掌握．
21．(8分）（2022秋·河北保定·八年级统考期末）图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
(1)图2中的阴影部分的正方形的边长等于___________；面积等于___________．
(2)观察图2，请你写出下列三个代数式(a+b)2，(a−b)2，ab之间的等量关系为___________．
(3)运用你所得到的公式，计算：若m、n为实数，且mn=5，m−n=4，试求m+n的值．
【答案】(1)a−b，a−b2 或a+b2−4ab
(2)a+b2−a−b2 =4ab
(3)±6
【分析】（1）根据图中给出的数据即可求得图乙中阴影部分正方形边长，根据正方形的面积公式求得面积；
（2）用两种不同方式求得阴影部分面积可得关于a+b2、a−b2、ab的等式；
（3）根据（2）中结论即可解题．
【详解】（1）图中阴影部分边长为a−b，
则阴影部分的面积为a−b2 或a+b2−4ab
故答案为：a−b；a−b2 或a+b2−4ab；
（2）用两种不同的方法表示阴影的面积：
方法一：阴影部分为边长=a−b的正方形，故面积=a−ba−b=a−b2；
方法二：阴影部分面积=a+b为边长的正方形面积−四个以a为长、b为宽的4个长方形面积=a+b2−4ab；
∴(a+b)2−4ab=(a−b)2；
即a+b2−a−b2 =4ab，
故答案为：a+b2−a−b2=4ab；
（3）由（2）得，m+n2−m−n2=4mn，
∴m+n2−42=20，
∴m+n = ± 6．
【点睛】本题考查了完全平方公式的计算，考查了正方形面积计算，本题中求得(a+b)2−4ab=(a−b)2是解题的关键．
22．(8分）（2022秋·辽宁铁岭·七年级统考期末）已知点О为直线AB上一点，将直角三角板MON的直角顶点放在点O上，并在∠MON内部作射线OC．
(1)如图l，三角板的一边OM与射线OA重合．
①∠AOC的余角是___________，补角是___________；
②若∠BOC=120°，则∠NOC的度数为___________；
(2)如图2，将三角板放置到如图位置，使OC恰好平分∠MOB，且∠BON=4∠NOC，求∠AOM的度数；
(3)若仍将三角板按照如图2的方式放置，仅满足OC平分∠MOB，试猜想∠AOM与∠NOC之间的数量关系为___________．
【答案】(1)①∠NOC，∠COB；②30°
(2)∠AOM=30°
(3)∠AOM=2∠NOC
【分析】（1）①根据余角和补角的定义进行解答即可；
②根据∠BOC=120°和∠BON=90°即可得出答案；
（2）设∠NOC=x，则∠BON=4x，根据OC恰好平分∠MOB，得出∠MOC=∠BOC=5x，根据∠MON=∠NOC+∠MOC=x+5x=90°列出方程，解方程，得出x的值，求出∠BOM=2∠BOC=2×5x=10x=150°，即可得出答案；
（3）设∠AOM=α，∠NOC=β，则∠MOC=90°−β，根据OC平分∠MOB，得出∠BOC=∠MOC=90°−β，根据∠AOM+∠BOM=180°，得出α+290°−β=180°，即可得出答案．
【详解】（1）解：①∵∠AOC+∠NOC=90°，∠AOC+∠BOC=180°，
∴∠AOC的余角是∠NOC，补角是∠COB；
故答案为：∠NOC，∠COB；
②∵∠MON=90°，
∴∠BON=180°−90°=90°，
∵∠BOC=120°，
∴∠NOC=120°−90°=30°，
故答案为：30°；
（2）解：设∠NOC=x，则∠BON=4x，
∴∠BOC=5x，
∵OC恰好平分∠MOB，
∴∠MOC=∠BOC=5x，
∴∠MON=∠NOC+∠MOC=x+5x=90°，
解得：x=15°，
∴∠BOM=2∠BOC=2×5x=10x=150°，
∴∠AOM=180°−∠BOM=30°；
（3）解：设∠AOM=α，∠NOC=β，则∠MOC=90°−β，
∵OC平分∠MOB，
∴∠BOC=∠MOC=90°−β，
∴∠MOB=290°−2β，
∵∠AOM+∠BOM=180°，
∴α+290°−β=180°，
整理得：α=2β，
∴∠AOM=2∠NOC．
故答案为：∠AOM=2∠NOC．
【点睛】本题主要考查了余角和补角的定义，角平分线的定义，解题的关键是数形结合，熟练掌握角平分线的定义．
23．(8分）（2022秋·四川宜宾·七年级统考期末）几何模型在解题中有着重要作用，例如美味的“猪蹄模型”．
(1)导入：如图①，已知AB∥CD∥EF，如果∠A=26°，∠C=34°，那么 ∠AEC= °；
(2)发现：如图②，已知AB∥CD，请判断∠AEC与∠A，∠C之间的数量关系，并说明理由；
(3)运用：(i)如图③，已知AB∥CD，∠AEC=88°，点M、N分别在AB、CD上，MN∥AE，如果∠C= 28°，那么∠MND= °；
(ii)如图④，已知AB∥CD，点M、N分别在AB、CD上， ME、NE分别平分∠AMF和∠CNF． 如果∠E=116°，那么∠F= °；
(iii)如图⑤，已知AB∥CD，点M、N分别在AB、CD上， MF、NG分别平分∠BME和∠CNE，且EG∥MF． 如果∠MEN=α，那么∠EGN= ．(用含α的代数式表示)
【答案】(1)60°
(2)∠AEC=∠A+∠C，理由见解析
(3)(i)120； (ii)128； (iii) 90°+12α
【分析】（1）根据平行线的性质得出∠A=∠AEF,∠C=∠FEC，进而根据∠AEC=∠AEF+∠CEF，即可求解；
（2）过点E作EF∥AB，根据（1）的方法即可求解；
（3）（i）由（2）可得∠AEC=∠A+∠C=88°，∠C= 28°，得出∠A=60°，根据∠MND=180°−∠BMN，即可求解；
（ii）由“猪蹄模型”，可得∠E=∠AME+∠CNE=116°，∠F=∠BMF+∠DNF，根据角平分线的性质得出∠AME=12∠AMF,∠CNE=12∠CNF，继而根据∠F=∠BMF+∠DNF=128°，即可求解；
（iii）如图所示，延长GE交AB于点H，设∠ENG =β，∠HME−θ，根据平行线的性质得出∠MHE=∠BMF=180−θ2=90°−θ2，α=θ+2β，根据∠EGN=∠GNC+∠AHE =∠GNC+∠AMF，即可得出结论．
【详解】（1）解：如图1，
∵AB∥CD∥EF
∴∠A=∠AEF,∠C=∠FEC
∵∠A=26°，∠C=34°，
∴∠AEC=∠AEF+∠CEF=∠A+∠B=26°+34°=60°
∴∠AEC= 60°
故答案为：60．
（2）∠AEC=∠A+∠C,
如图所示，过点E作EF∥AB，
∵ EF∥AB，
∴ ∠A= ∠AEF，
∵ EF∥AB，AB∥CD，
∴ EF∥CD，
∴ ∠FEC=∠C ，
∴∠AEC=∠AEF+∠FEC=∠A+∠C；
（3）解：（i）由（2）可得∠AEC=∠A+∠C=88°，∠C= 28°，
∴∠A=60°，
∵MN∥AE，
∴∠BMN=∠A=60°，
∵AB∥CD，
∴∠MND=180°−∠BMN=180°−60°=120°，
故答案为：120．
（ii）解：如图所示，∵AB∥CD
由“猪蹄模型”，可得∠E=∠AME+∠CNE=116°，∠F=∠BMF+∠DNF；
∵ME、NE分别平分∠AMF和∠CNF
∴∠AME=12∠AMF,∠CNE=12∠CNF
∴∠AMF+∠CNF=116°×2=232°
∴∠MBF+∠DNF=360°−232°=128°，
∴∠F=∠BMF+∠DNF=128°,
故答案为：128．
（iii）解：如图所示，延长GE交AB于点H，
设∠ENG =β，∠HME−θ
∵MF、NG分别平分∠BME和∠CNE，
∴∠BMF=12∠BME=12180°−θ=90°−θ2,∠CNE=2∠ENG=2β，
∵HG∥MF
∴∠MHE=∠BMF=180−θ2=90°−θ2，
∵AB∥CD
∴∠MEN=∠AME+∠CNE，
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
x
…
1
2
3
4
…
y
…
12
14
16
18
…
所挂物体质量xkg
0
1
2
3
4
弹簧长度ycm
16
18
20
22
24