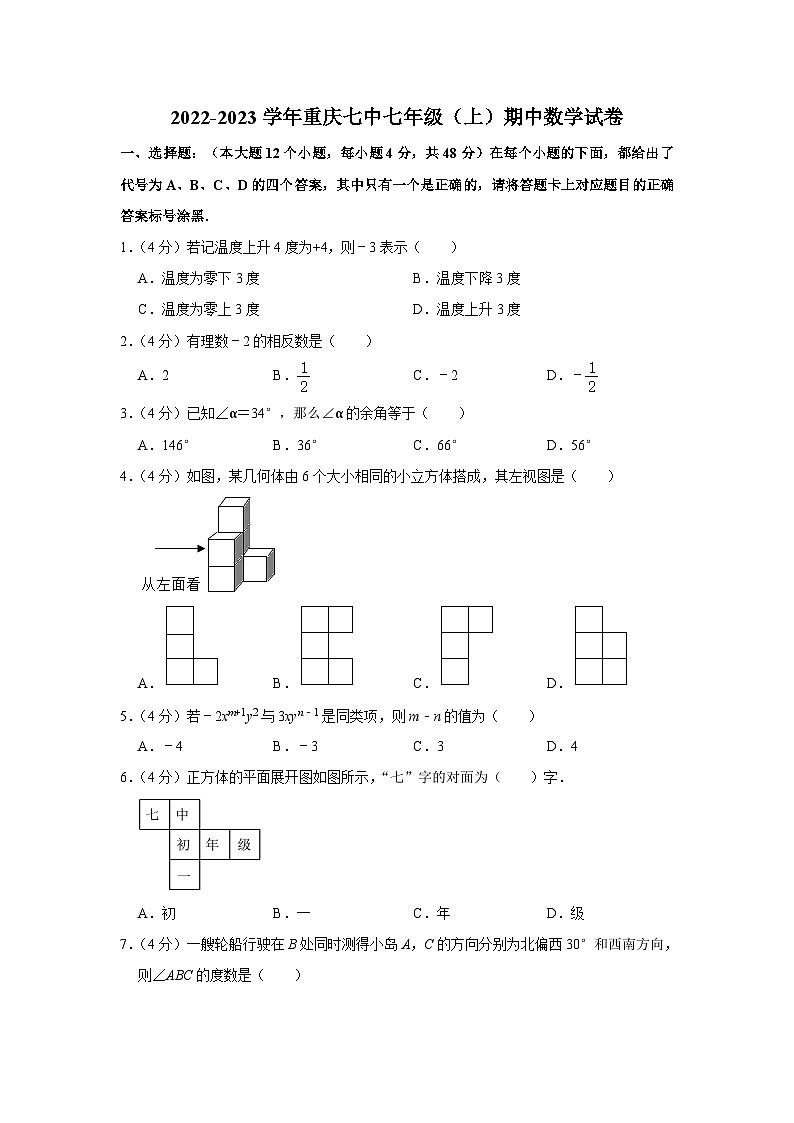
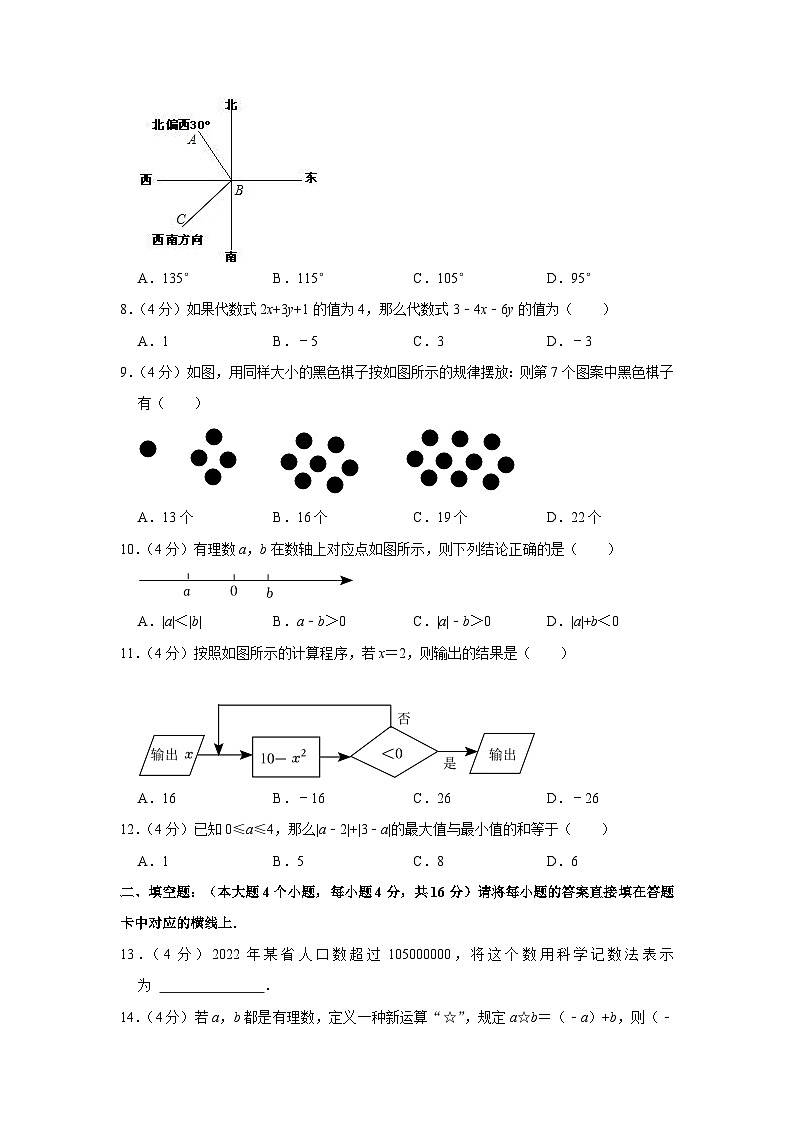
华师版2022-2023学年重庆七中七年级（上）期中数学试卷(含答案)

这是一份华师版2022-2023学年重庆七中七年级（上）期中数学试卷(含答案)，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（4分）若记温度上升4度为+4，则﹣3表示（ ）
A．温度为零下3度B．温度下降3度
C．温度为零上3度D．温度上升3度
2．（4分）有理数﹣2的相反数是（ ）
A．2B．C．﹣2D．﹣
3．（4分）已知∠α＝34°，那么∠α的余角等于（ ）
A．146°B．36°C．66°D．56°
4．（4分）如图，某几何体由6个大小相同的小立方体搭成，其左视图是（ ）
A．B．C．D．
5．（4分）若﹣2xm+1y2与3xyn﹣1是同类项，则m﹣n的值为（ ）
A．﹣4B．﹣3C．3D．4
6．（4分）正方体的平面展开图如图所示，“七”字的对面为（ ）字．
A．初B．一C．年D．级
7．（4分）一艘轮船行驶在B处同时测得小岛A，C的方向分别为北偏西30°和西南方向，则∠ABC的度数是（ ）
A．135°B．115°C．105°D．95°
8．（4分）如果代数式2x+3y+1的值为4，那么代数式3﹣4x﹣6y的值为（ ）
A．1B．﹣5C．3D．﹣3
9．（4分）如图，用同样大小的黑色棋子按如图所示的规律摆放：则第7个图案中黑色棋子有（ ）
A．13个B．16个C．19个D．22个
10．（4分）有理数a，b在数轴上对应点如图所示，则下列结论正确的是（ ）
A．|a|＜|b|B．a﹣b＞0C．|a|﹣b＞0D．|a|+b＜0
11．（4分）按照如图所示的计算程序，若x＝2，则输出的结果是（ ）
A．16B．﹣16C．26D．﹣26
12．（4分）已知0≤a≤4，那么|a﹣2|+|3﹣a|的最大值与最小值的和等于（ ）
A．1B．5C．8D．6
二、填空题：（本大题4个小题，每小题4分，共16分）请将每小题的答案直接填在答题卡中对应的横线上．
13．（4分）2022年某省人口数超过105000000，将这个数用科学记数法表示为 ．
14．（4分）若a，b都是有理数，定义一种新运算“☆”，规定a☆b＝（﹣a）+b，则（﹣2）☆4的值为 ．
15．（4分）如图，已知点C为AB上一点，AC＝12cm，CB＝AC，D、E分别为AC、AB的中点；则DE的长为 cm．
16．（4分）设一列数a1、a2、a3、…a2021中任意三个相邻数之和都是18，已知a6＝15，a14＝2x，a31＝x+3，那么a2021＝ ．
三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡中对应的位置上．
17．（8分）计算：
（1）﹣2+（﹣3）﹣（﹣5）；
（2）32×（﹣4）÷6．
18．（8分）计算：
（1）5x﹣3x2+4x2+6x；
（2）4（a2+b2）﹣（3a2﹣5b2）．
四、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答书写在答题卡中对应的位置上．
19．（10分）计算：．
（10分）先化简，再求值：，其中x是最大的负整数，y是绝对值最小的正整数．
21．（10分）2017年9月11日，以“绿色生活•从你我做起”为主题的重庆市第四届生态文明知识竞赛活动正式启动．某校组织全校学生参与后，王老师抽取了班上第一大组8名学生的成绩，若以80分为标准，超过的分数用正数表示，不足的分数用负数表示，成绩记录如下：﹣3，+7，﹣12，+18，+6，﹣5，﹣21，+14
（1）最高分比最低分多多少分？第一大组平均每人得多少分？
（2）若规定：成绩高于80分的学生操行分每人加3分，成绩在60～80分的学生操行分每人加2分，成绩在60分以下的学生操行分每人扣1分，那么第一大组的学生共加操行分多少分？
22．（10分）如图是某居民小区的一块长为a米，宽为2b米的长方形空地为了美化环境，准备在这个长方形空地的四个顶点处修建一个半径为b米的扇形花台，然后在花台内种花，其余种草．如果建造花台及种花的费用为每平方米100元，种草的费用为每平方米50元．
（1）求美化这块空地共需多少元？（用含有a，b，π的式子表示）
（2）当a＝6，b＝2，π取3时，美化这块空地共需多少元？
23．（10分）如图，O为直线AB上一点，∠DOE＝90°，OF平分∠BOD．
（1）若∠AOE＝20°，则∠BOF＝ ；
（2）若∠BOF是∠AOE的5倍，求∠AOE度数．
24．（10分）对每个数位数字均不为零且互不相等的一个三位正整数x，若将x的十位数字与百位数字交换位置，得到一个新的三位数y，我们称y为x的“置换数”，如：123的“置换数”为“213”；若由x的百位、十位、个位上的数字任选两个组成一个新的两位数，所有新的两位数之和记为z，我们称z为x的“衍生数”．如456：因为45+46+54+56+64+65＝330，所以456的“衍生数”为330．
（1）直接写出987的“置换数”，并求987的“衍生数”；
（2）对每个数位数字均不为零且互不相等的一个三位正整数x，设十位数字为1，若x的“衍生数”与x的“置换数”之差为102，求x．
25．（10分）如图，A，B（A在B的左侧）是数轴上的两点，点A对应的数为﹣4，且AB＝10，动点P从点A出发，以每秒3个单位长度的速度沿数轴向左运动，同时动点Q从点B出发，以每秒5个单位长度的速度沿数轴向左运动，在点P，Q的运动过程中，M，N始终为AP，BQ的中点，设运动时间为t（t＞0）秒．
（1）当P，Q重合时，求t的值；
（2）当MN＝AB时，求t的值；
（3）当AP＝2AB时，点P，Q停止运动，此时点M，N也随之停止运动，将线段MN沿数轴以每秒2个单位长度的速度滑动，从此刻开始，经过t秒后满足AM＝BN时，求t的值．
参考答案与试题解析
一、1~5：BADDB 6~10：CCDCC 11~12：DD
二、13．1.05×108 14．6 15．4 16．0
三、17．解：（1）﹣2+（﹣3）﹣（﹣5）
＝﹣5+5
＝0；
（2）32×（﹣4）÷6
＝9×4×
＝6．
18．解：（1）原式＝（﹣3+4）x2+（5+6）x
＝x2+11x；
（2）原式＝4a2+4b2﹣3a2+5b2
＝（4﹣3）a2+（4+5）b2
＝a2+9b2．
四、19．解：原式＝（﹣+﹣）×36﹣（﹣4）2×（﹣1+1）
＝﹣×36+×36﹣×36﹣16×
＝﹣27+20﹣21﹣14
＝﹣42．
20．解：∵x是最大的负整数，y是绝对值最小的正整数，
∴x＝﹣1，y＝1，
∴
＝2x2y﹣4xy2﹣（﹣x2y2+4x2y﹣2xy2+x2y2）
＝2x2y﹣4xy2+x2y2﹣4x2y+2xy2﹣x2y2
＝﹣2x2y﹣2xy2
＝﹣2×（﹣1）2×1﹣2×（﹣1）×12
＝﹣2+2
＝0．
∴化简后结果为：﹣2x2y﹣2xy2，值为：0．
21．解：（1）最高分比最低分多（+18）﹣（﹣21）＝39分；
80+（﹣3+7﹣12+18+6﹣5﹣21+14）＝80.5，
即第一大组平均每人得80.5分；
（2）∵成绩高于80分的学生有4人，成绩在60～80分的学生有3人，成绩在60分以下的学生有1人，
∴4×3+3×2﹣1＝17，
即第一大组的学生共加操行分17分．
22．解：（1）∵一个花台为圆，
∴四个花台的面积为一个圆的面积，即：πb2，
∴其余部分的面积为：2b•a﹣πb2，
∴美化这块空地共需费用：100×πb2+50（2ba﹣πb2）＝100ab+50πb2（元）．
∴美化这块空地共需（100ab+50πb2）元．
（2）将a＝6，b＝2，π＝3代入（1）中所得的代数式得：
100ab+50πb2
＝100×6×2+50×3×22
＝1200+600
＝1800（元）．
∴美化这块空地共需1800元．
23．解：（1）∵∠DOE＝90°，∠AOE＝20°，
∴∠AOD＝∠DOE﹣∠AOE＝90°﹣20°＝70°．
∴∠BOD＝180°﹣∠AOD＝180°﹣70°＝110°．
∵OF平分∠BOD．
∴．
故答案为：55°．
（2）设∠AOE＝x，
则∠BOF＝5x．
∴∠AOD＝90°﹣x．
∠BOD＝180°﹣（90°﹣x）＝90°+x．
∵OF平分∠BOD，
∴．
∴，
即
∴，
∴∠AOE＝10°．
24．解：（1）987的“置换数”为897，
因为98+97+89+87+79+78＝528，
所以987的“衍生数”为528；
（2）根据题意可知：
设三位正整数x为：100b+10+a，
所以x的“衍生数”为：
10b+1+10b+a+10+b+10+a+10a+b+10a+1＝22b+22a+22，
x的“置换数”为：100+10b+a，
所以22b+22a+22﹣（100+10b+a）＝102
所以或，
所以x＝814或118．
因为每个数位数字均不为零，且互不相等，
所以x＝814．
25．解：（1）∵点A对应的数为﹣4，且AB＝10，
∴B表示的数是6，
∵动点P从点A出发，以每秒3个单位长度的速度沿数轴向左运动，同时动点Q从点B出发，以每秒5个单位长度的速度沿数轴向左运动，运动时间为t（t＞0）秒，
∴P表示的数是﹣4﹣3t，Q表示的数是6﹣5t，
解﹣4﹣3t＝6﹣5t得t＝5，
∴当P，Q重合时，t的值是5；
（2）∵点A对应的数为﹣4，P表示的数是﹣4﹣3t，M是AP的中点，
∴M表示的数是＝﹣4﹣t，
同理N表示的数是6﹣t，
∵MN＝AB，
∴|（﹣4﹣t）﹣（6﹣t）|＝10，
解得t＝0（舍去）或t＝20，
∴当MN＝AB时，t的值是20；
（3）∵AP＝2AB，
∴3t＝2×10，
解得t＝，
此时M表示的数为﹣4﹣t＝﹣4﹣×＝﹣14，N表示的数是6﹣t＝6﹣×＝﹣，
①若MN向左滑动t'秒，则M表示的数是﹣14﹣2t'，N表示的数是﹣﹣2t'，
∴AM＝﹣4﹣（﹣14﹣2t'）＝10+2t'，BN＝6﹣（﹣﹣2t'）＝+2t'，
∴10+2t'＝（+2t'），
解得t'＝﹣（舍去），
②若MN向右滑动t'秒，则M表示的数是﹣14+2t'，N表示的数是﹣+2t'，
∴AM＝|﹣4﹣（﹣14+2t'）|＝|10﹣2t'|，BN＝|6﹣（﹣+2t'）|＝|﹣2t'|，
∴|10﹣2t'|＝|﹣2t'|，
解得t'＝或t'＝，
∴从此刻开始，经过t秒后满足AM＝BN时，t的值是或．