四川省内江市第一中学2024-2025学年高一上学期开学考试数学试题（Word版附解析）

这是一份四川省内江市第一中学2024-2025学年高一上学期开学考试数学试题（Word版附解析），文件包含四川省内江市第一中学2024-2025学年高一上学期开学考试数学试题Word版含解析docx、四川省内江市第一中学2024-2025学年高一上学期开学考试数学试题Word版无答案docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

注意事项：
1.答题前，考生务必将自己的姓名、座位号、准考证号用0.5毫米的黑色，墨迹签字笔填写在答题卡上.
2.选择题使用2B铅笔涂在答题卡对应题目标号的位置上；非选择题用0.5毫米，黑色墨迹签字笔书写在答题卡对应题目标号的答题区域内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效.
3.考试结束后，由监考教师将答题卡收回，试题卷和草稿纸由学生保管，以便后续分析.
一、选择题（每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）
1. 下列各式正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】根据指数幂运算求解.
【详解】对A：原式，所以A选项错误；
对B：原式，所以B选项错误；
对C：原式，所以C选项错误；
对D：显然，所以原式，所以D选项正确.
故选：D
2. 若二次根式有意义，则的取值范围是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据开偶数次方根号里的数大于等于零即可得解.
【详解】若二次根式有意义，
则，解得.
故选：C.
3. 把分解因式的结果是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】根据完全平方公式并提取公因式即可得出结果.
【详解】易知,
故选：A
4. 某班级有20个女同学，22个男同学，班上每个同学的名字都写在一张小纸条上放入一个盒子搅匀如果老师随机地从盒子中取出1张纸条，则下列命题中正确的是（ ）
A. 抽到男同学名字的可能性是
B. 抽到女同学名字的可能性是
C. 抽到男同学名字的可能性小于抽到女同学名字的可能性
D. 抽到男同学名字的可能性大于抽到女同学名字的可能性
【答案】D
【解析】
【分析】根据随机事件的概率逐项分析判断.
【详解】对于选项A：抽到男同学名字的可能性是，故A错误；
对于选项B：抽到女同学名字的可能性是，故B错误；
对于选项C、D：因为，所以抽到男同学名字的可能性大于抽到女同学名字的可能性，
故C错误，D正确；
故选：D.
5. 在平面直角坐标系中，将抛物线先向左平移3个单位长度，再向下平移4个单位长度，所得到的抛物线的表达式为（ ）
A. B.
C D.
【答案】D
【解析】
【分析】由图象的平移变化规则即可得出答案.
【详解】将抛物线先向左平移3个单位长度，可得：，
再向下平移4个单位长度，可得.
故选：D.
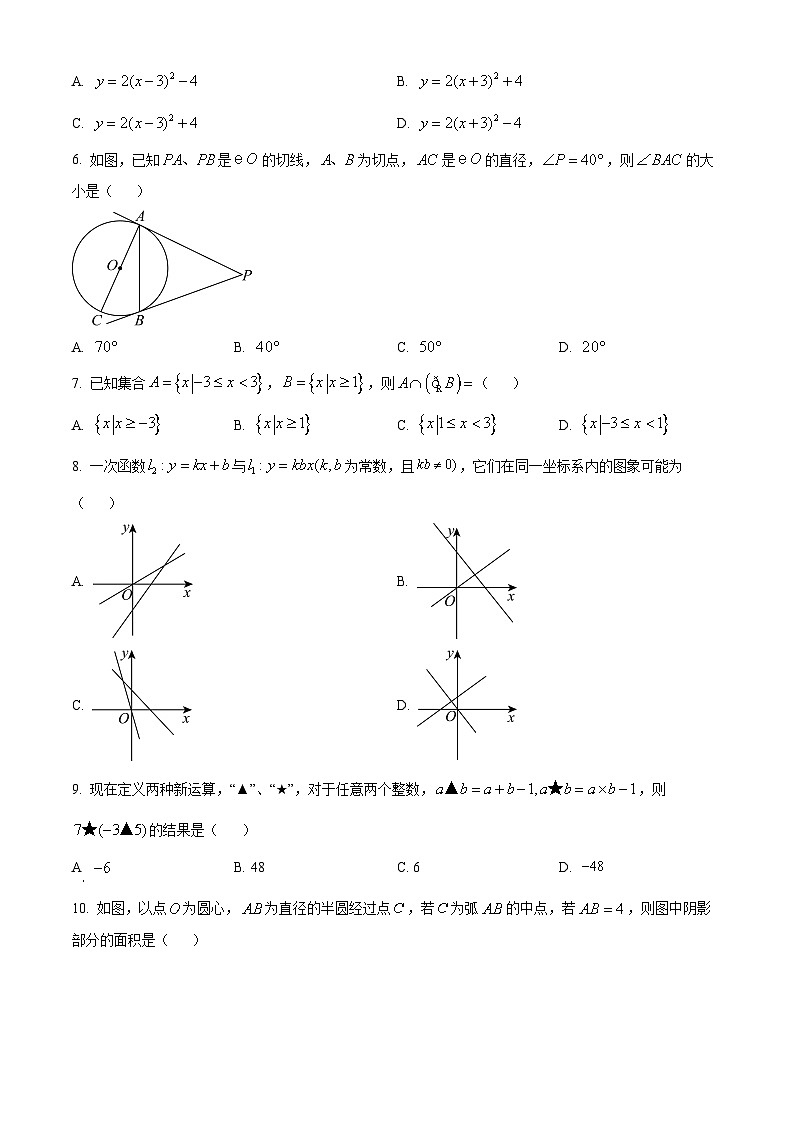
6. 如图，已知是的切线，为切点，是的直径，，则的大小是（ ）

A. B. C. D.
【答案】D
【解析】
【分析】连接，先求出，再根据即可得解.
【详解】连接，
因为是的切线，所以，
又，则，
因为，所以.
故选：D.

7. 已知集合，，则（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据集合交集，补集运算解决即可.
【详解】由题知，集合，，
所以，
所以，
故选：D
8. 一次函数与为常数，且，它们在同一坐标系内的图象可能为（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】根据图象分析b、k取值符号进行判断即可．
【详解】对于选项A中，直线的直线的∴A错；
对于选项B中，直线的直线的，∴B错；
对于选项C中，直线的直线的∴C对；
对于选项D中，直线的直线的∴D错．
故选：C．
9. 现在定义两种新运算，“▲”、“★”，对于任意两个整数，，则的结果是（ ）
A. B. 48C. 6D.
【答案】C
【解析】
【分析】根据题意直接运算求解即可.
【详解】由题意可得：.
故选：C.
10. 如图，以点为圆心，为直径的半圆经过点，若为弧的中点，若，则图中阴影部分的面积是（ ）

A. B. C. 2D.
【答案】A
【解析】
【分析】由对称性可知，阴影部分面积为以为圆心，为直径的圆的面积的，由圆的面积公式即可求解.
【详解】如题图，由对称性可知，阴影部分面积为以为圆心，为直径的圆的面积的，
由题意圆的半径，
所以阴影部分的面积为.
故选：A.
11. 已知不等式的解集为，则不等式的解集为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据一元二次不等式的解集性质，结合解一元二次不等式的方法进行求解即可.
【详解】因为不等式的解集为，
所以有，
由，或，
故选：A
12. 若实数，且a，b满足，，则代数式的值为（ ）
A. 2B. －20C. 2或－20D. 2或20
【答案】B
【解析】
【分析】
利用韦达定理可求的值.
【详解】因为，，故为方程的两个根，
故
又
，
故选：B.
【点睛】本题考查一元二次方程的解、韦达定理，注意利用同构的思想来构建方程，另外注意将代数式整合成与两根和、两根积有关的代数式，本题属于基础题.
二、填空题（每小题5分，共20分.）
13. 5G是第五代移动通信技术，5G网络下载速度可以达到每秒1300000以上，这意味着下载一部高清电影只需1秒，将1300000用科学记数法表示应为______．
【答案】
【解析】
【分析】借助科学记数法定义即可得.
【详解】.
故答案为：.
14. 若，则______.
【答案】
【解析】
【分析】根据题意可得，运算求解即可.
【详解】因为，则，解得，
所以.
故答案：.
15. 如图，的直径是的弦，，垂足为，且，则______.

【答案】
【解析】
【分析】根据题意结合垂径定理运算求解.
【详解】由题意可得：的半径，则，
所以.
故答案为：.
16. 已知函数，计算_________．
【答案】
【解析】
【分析】先求出，再观察所求，倒序相加即可得解.
【详解】由，
得，
所以
.
故答案为：.
三、解答题（共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）
17. （1）；
（2）先化简，再求值：，其中.
【答案】（1）2；（2）.
【解析】
【分析】（1）应用根式、绝对值运算化简求值即可；
（2）应用通分、因式分解化简目标式，最后代入求值即可.
【详解】（1）解：；
（2）原式，又，
所以原式.
18. 创建文明城市，构建美好家园.为提高垃圾分类意识，幸福社区决定采购购买个型垃圾桶和个型垃圾桶共需要元，购买个型垃圾桶和个型垃圾桶共需要元.
（1）求每个型垃圾桶和每个型垃圾桶各为多少元；
（2）若需购买，两种型号的垃圾桶共个，总费用不超过元，至少需购买型垃圾桶多少个？
【答案】（1）每个型垃圾桶为元，每个型垃圾桶为元
（2）至少需购买型垃圾桶个
【解析】
【分析】（1）根据题意构造二元一次方程组即可求得结果；
（2）设购买的型垃圾桶为个，利用总费用可构造不等式求得结果.
【小问1详解】
设型垃圾桶的价格为元/个，型垃圾桶的价格为元/个，
由题意可得：，解得：，，
每个型垃圾桶为元，每个型垃圾桶为元.
【小问2详解】
设购买的型垃圾桶为个，则购买的型垃圾桶为个，
由题意知：，解得：，，
即至少需购买型垃圾桶个.
19. 自我校深化课程改革以来，初中数学校本课程开设了：A.利用影长求物体高度；.制作视力表；.设计遮阳棚；.池塘里有多少条鱼.四类数学实践活动选修课，供学生们选择，其中九年级11班和12班的两个班的同学将选择结果绘制成如右两幅不完整的统计图.根据图中信息解决下列问题：
学生选修数学实践活动课条形统计图 学生选修数学实践活动课扇形统计图

（1）本次共______名学生选修了数学实践活动课，扇形统计图中所对应的扇形的圆心角为______度；
（2）补全条形统计图；
（3）选修类数学实践活动的学生中有2名女生和2名男生表现出色，现从4人中随机抽取2人来帮助学校设计遮阳棚，请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
【答案】（1）60，144
（2）答案见解析 （3）
【解析】
【分析】（1）分析条形统计图和扇形统计图，从而求出本次调查的学生人数，并求出所对应的扇形的圆心角；
（2）根据调查的总人数和A类别所在比例求出A类别人数，再求出D类别人数，补全条形统计图；
（3）画出树状图，得到共有12种等可能的结果数，其中所抽取的两人恰好是1名女生和1名男生的结果数，从而求出相应的概率.
【小问1详解】
从条形统计图中得到类别有12人，从扇形统计图中得到类别占比为，
故本次调查的学生人数为（名），
则扇形统计图中所对应的扇形的圆心角为
【小问2详解】
A类别人数为（人），
则类别人数为（人），
∴补全条形统计图为
【小问3详解】
画树状图为：
共有12种等可能的结果数，
其中所抽取的两人恰好是1名女生和1名男生的结果数为8，
所以所抽取的两人恰好是1名女生和1名男生的概率为.
20. 问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图，已知是的角平分线，则可证．小慧的证明思路是：如图，过点作，构造相似三角形来证明．尝试证明：

（1）请参照小慧提供的思路，利用图证明：；
（2）应用拓展：如图，在中，，将沿所在直线折叠，点恰好落在边上的点处．
①若，，求的长；
②若，，求的长（用含的式子表示）
【答案】（1）证明见解析
（2）①；②
【解析】
【分析】（1）利用∽和可推导得到结论；
（2）①由（1）中结论可推导得到，结合勾股定理和可得到结果；
②利用三角函数表示出，结合①的方法即可求得结果.
【小问1详解】
，，又，
∽，；
平分，，又，
，，.
【小问2详解】
①由翻折条件可知：平分，；
由（1）得：，又，，，
，，即，
；
②，，，，，
由翻折条件可知：平分，；
由（1）得：，即，
，.
21. 已知一次函数与轴交于点，且过点，回答下列问题．
（1）求该一次函数解析式；
（2）一次函数的解析式也称作该直线的斜截式方程，如解析式我们只需要将向右移项就可以得到，将前的系数替代为未知数，将前的系数1替代为未知数，将常数项替代为未知数，即可得到方程，该二元一次方程也称为直线的一般方程（其中一般为非负整数，且）．一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：
点到直线的距离公式是：
如：求：点到直线的距离．
解：先将该解析式整理为一般方程：
(I)移项
(II)将化为非负整数即得一般式方程：
由点到直线的距离公式，得
①根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．
已知（1）中的解析式代表的直线与直线平行，试求这两条直线间距离；
②已知一动点（为未知实数），记为点到直线的距离（点不在该直线上），求的最小值．
【答案】（1）
（2）①，②
【解析】
【分析】（1）将点代入解方程组即可；
（2）①在直线上取一点，由点到直线的距离公式计算即可；
②由点到线的距离公式得，再通过二次函数求最小值即可.
【小问1详解】
将点代入得
，解得，
所以一次函数的解析式为.
【小问2详解】
①由（1）得一次函数解析式为，
转化为，且与，
在直线上取一点，
则点到直线的距离为.
②根据点到直线的距离公式得，
当时，.
22. 如图，抛物线与轴交于点，与轴交于点.

（1）求抛物线的解析式；
（2）连接，点为线段上的一个动点，过点作轴的平行线交抛物线于点，设点的横坐标为，线段长度为.求与的函数关系式（不要求写出自变量的取值范围）；
（3）在（2）的条件下，连接，是否存在值，使是等腰三角形？若存在，求出的值；若不存在，请说明理由.
【答案】（1）
（2）
（3）存在，或或
【解析】
【分析】（1）直接将两点坐标代入抛物线的表达式解方程组即可求得；
（2）根据两点坐标求得直线的解析式，根据点横标分别求得两点纵标，上下两点纵标之差即为线段的长度；
（3）因为不清楚等腰三角形中哪两条边相等，所以要分为三种情况分别讨论，即或或.
【小问1详解】
∵，
∴，解得，
∴该抛物线的解析式是
【小问2详解】
设直线的解析式为

∵，
∴，即
∴直线的解析式为
∵轴，∴、两点的横坐标都为.
在中，当时，
∴
中，当时，
∴，
∴
【小问3详解】
存在.证明如下：
∵，
∴，，即
过点作轴于点，

∴，∴，
∴，
若是等腰三角形，则分以下情况讨论：
①时，则整理得
解得：或
∵不与重合，∴舍去∴；
（2）时，过点作于点，

∴
∵轴，∴，
∴，
∴，∴，
∴.又∵，∴
则
整理得，解得：或
∵不与重合，∴舍去∴；
③时，过点作于点，

∵，
∴为中点，且点坐标为，点纵坐标为，
由第二问知点坐标为，
∵
∴，
整理得，解得或，
∵不与重合，∴舍去，
∴.
综上：存在的值，或或使得是等腰三角形.