高考数学第一轮复习导学案(新高考)第57讲立体几何中翻折问题(微专题)(原卷版+解析)

这是一份高考数学第一轮复习导学案(新高考)第57讲立体几何中翻折问题(微专题)(原卷版+解析)，共17页。学案主要包含了题型选讲，折叠问题，折叠的综合性问题等内容，欢迎下载使用。

题型一 、展开问题
例1、（2022·广东佛山·高三期末）长方体中，，E为棱上的动点，平面交棱于F，则四边形的周长的最小值为（ ）
A．B．C．D．
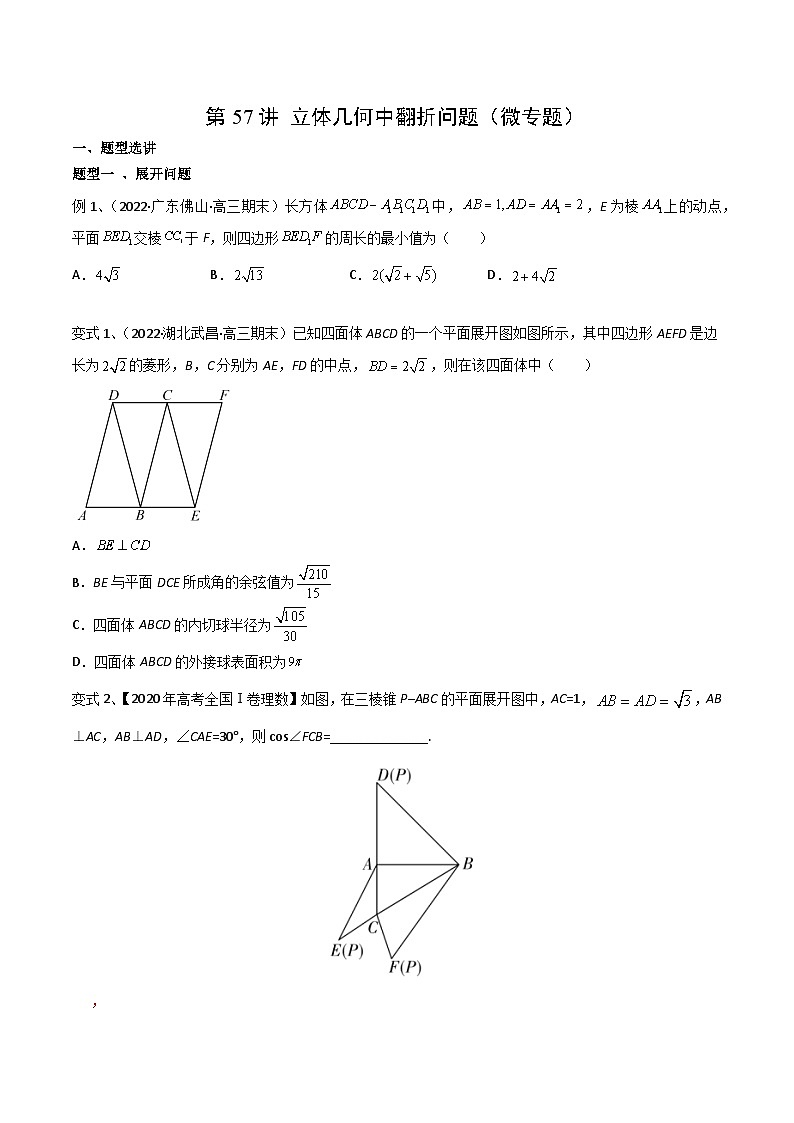
变式1、（2022·湖北武昌·高三期末）已知四面体ABCD的一个平面展开图如图所示，其中四边形AEFD是边长为的菱形，B，C分别为AE，FD的中点，，则在该四面体中（ ）
A．
B．BE与平面DCE所成角的余弦值为
C．四面体ABCD的内切球半径为
D．四面体ABCD的外接球表面积为
变式2、【2020年高考全国Ⅰ卷理数】如图，在三棱锥P–ABC的平面展开图中，AC=1，，AB⊥AC，AB⊥AD，∠CAE=30°，则cs∠FCB=______________.
，
题型二、折叠问题
例2、（2022·河北唐山·高三期末）如图，四边形ABCD是边长为2的正方形，E为AB的中点，将沿DE所在的直线翻折，使A与重合，得到四棱锥，则在翻折的过程中（ ）
A．B．存在某个位置，使得
C．存在某个位置，使得D．存在某个位置，使四棱锥的体积为1
变式1、（2022·江苏宿迁·高三期末）如图，一张长､宽分别为的矩形纸，，分别是其四条边的中点.现将其沿图中虚线折起，使得四点重合为一点，从而得到一个多面体，则（ ）
A．在该多面体中，
B．该多面体是三棱锥
C．在该多面体中，平面平面
D．该多面体的体积为
变式2、（2022·江苏海安·高三期末）如图，ABCD是一块直角梯形加热片，AB∥CD，∠DAB＝60°，AB＝AD＝4 dm．现将△BCD沿BD折起，成为二面角A－BD－C是90°的加热零件，则AC间的距离是________dm；为了安全，把该零件放进一个球形防护罩，则球形防护罩的表面积的最小值是________dm2．（所有器件厚度忽略不计）
变式3、（2022·河北保定·高三期末）如图，是边长为4的等边三角形的中位线，将沿折起，使得点与重合，平面平面，则四棱雉外接球的表面积是___________.
题型三、折叠的综合性问题
例3、（2022·江苏扬州·高三期末）在边长为6的正三角形ABC中M，N分别为边AB，AC上的点，且满足，把△AMN沿着MN翻折至A′MN位置，则下列说法中正确的有（ ）
A．在翻折过程中，在边A′N上存在点P，满足CP∥平面A′BM
B．若，则在翻折过程中的某个位置，满足平面A′BC⊥平面BCNM
C．若且二面角A′－MN－B的大小为120°，则四棱锥A′－BCNM的外接球的表面积为61π
D．在翻折过程中，四棱锥A′－BCNM体积的最大值为
变式1、（2021·山东滨州市·高三二模）已知正方形的边长为2，将沿AC翻折到的位置，得到四面体，在翻折过程中，点始终位于所在平面的同一侧，且的最小值为，则下列结论正确的是（ ）
A．四面体的外接球的表面积为
B．四面体体积的最大值为
C．点D的运动轨迹的长度为
D．边AD旋转所形成的曲面的面积为
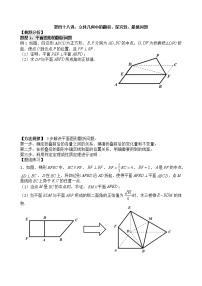
变式2、【2022·广东省深圳市宝安区第一次调研10月】如图甲是由正方形，等边和等边组成的一个平面图形，其中，将其沿，，折起得三棱锥，如图乙.
（1）求证：平面平面；
（2）过棱作平面交棱于点，且三棱锥和的体积比为，求直线与平面所成角的正弦值.
第57讲 立体几何中翻折问题（微专题）
一、题型选讲
题型一 、展开问题
例1、（2022·广东佛山·高三期末）长方体中，，E为棱上的动点，平面交棱于F，则四边形的周长的最小值为（ ）
A．B．C．D．
【答案】B
【分析】
将几何体展开，利用两点之间直线段最短即可求得截面最短周长．
【详解】
解：将长方体展开，如图所示：
当点为与的交点，为与的交点时，截面四边形的周长最小，
最小值为．
故选：B．
变式1、（2022·湖北武昌·高三期末）已知四面体ABCD的一个平面展开图如图所示，其中四边形AEFD是边长为的菱形，B，C分别为AE，FD的中点，，则在该四面体中（ ）
A．
B．BE与平面DCE所成角的余弦值为
C．四面体ABCD的内切球半径为
D．四面体ABCD的外接球表面积为
【答案】ACD
【分析】
几何体内各相关线段的计算即可.
【详解】
由题意得，展开图拼成的几何体如下图所示，
， ，
取AB中点M，CD中点N，MN中点O，连MN、OA，
过O作 于H，
则OH是内切球的半径，OA是外接球的半径.
所以，

对于A：
，，，故 平面ABN，而平面ABN ，所以 ，故A正确；
对于B：
由于 平面ACD，故平面ABN平面ACD，故 是BE与平面DCE所成角，
故 ，故B错误；
对于C：
，故C正确；
对于D：

所以外接球的表面积为 ，故D正确.
故选：ACD
变式2、【2020年高考全国Ⅰ卷理数】如图，在三棱锥P–ABC的平面展开图中，AC=1，，AB⊥AC，AB⊥AD，∠CAE=30°，则cs∠FCB=______________.
【答案】
【解析】，，，
由勾股定理得，
同理得，，
在中，，，，
由余弦定理得，
，
在中，，，，
由余弦定理得.
故答案为：.
题型二、折叠问题
例2、（2022·河北唐山·高三期末）如图，四边形ABCD是边长为2的正方形，E为AB的中点，将沿DE所在的直线翻折，使A与重合，得到四棱锥，则在翻折的过程中（ ）
A．B．存在某个位置，使得
C．存在某个位置，使得D．存在某个位置，使四棱锥的体积为1
【答案】AB
【分析】
过作，垂足为，证得平面，可判定A正确；取的中点，连接，当在平面上的投影在上时，可判定B正确；连接，由直线与是异面直线，可判定C错误；求得，结合体积公式求可判定D错误.
【详解】
对于A中，如图所示，过作，垂足为，延长交于点，
因为，且，所以平面，
又因为平面，所以，所以A正确；
对于B中，取的中点，连接，当在平面上的投影在上时，此时平面，从而得到，所以B正确；
对于C中，连接，因为平面，平面，
所以直线与是异面直线，所以不存在某个位置，使得，所以C错误；
对于D中，由，解得，
由作，可得，
即此时四棱锥的高，此时，
所以不存在某个位置，使四棱锥的体积为1，所以D错误.
故选：AB.
变式1、（2022·江苏宿迁·高三期末）如图，一张长､宽分别为的矩形纸，，分别是其四条边的中点.现将其沿图中虚线折起，使得四点重合为一点，从而得到一个多面体，则（ ）
A．在该多面体中，
B．该多面体是三棱锥
C．在该多面体中，平面平面
D．该多面体的体积为
【答案】BCD
【分析】
利用图形翻折，结合勾股定理，确定该多面体是以为顶点的三棱锥，利用线面垂直，判定面面垂直，以及棱锥的体积公式即可得出结论．
【详解】
由于长、宽分别为，1，
分别是其四条边的中点，
现将其沿图中虚线折起，
使得四点重合为一点，且为的中点，
从而得到一个多面体，
所以该多面体是以为顶点的三棱锥，故B正确；
，，，故A不正确；
由于，所以，
，可得平面，
则三棱锥的体积为，故D正确；
因为，，所以平面，
又平面，可得平面平面，故C正确.
故选：BCD
变式2、（2022·江苏海安·高三期末）如图，ABCD是一块直角梯形加热片，AB∥CD，∠DAB＝60°，AB＝AD＝4 dm．现将△BCD沿BD折起，成为二面角A－BD－C是90°的加热零件，则AC间的距离是________dm；为了安全，把该零件放进一个球形防护罩，则球形防护罩的表面积的最小值是________dm2．（所有器件厚度忽略不计）
【答案】4
【分析】
设E为BD的中点，由题可得AE⊥平面BCD，进而可求，再结合条件可得△DAB的中心为棱锥的外接球的球心，即求.
【详解】
∵ABCD是一块直角梯形加热片，AB∥CD，∠DAB＝60°，AB＝AD＝4 dm．
∴△DAB为等边三角形，，
设E为BD的中点，连接AE，CE，则AE⊥BD，又二面角A－BD－C是90°，
∴AE⊥平面BCD，CE平面BCD，
∴AE⊥CE，又CE=2 dm，，
∴，
设△DAB的中心为O，则OE⊥平面BCD，又E为BD的中点，△BCD为直角三角形，
∴OB=OC=OD=OA，即O为三棱锥的外接球的球心，
又，
故球形防护罩的表面积的最小值为.
故答案为：4，.
变式3、（2022·河北保定·高三期末）如图，是边长为4的等边三角形的中位线，将沿折起，使得点与重合，平面平面，则四棱雉外接球的表面积是___________.
【答案】
【分析】
求出四边形外接圆的圆半径，再设四棱锥外接球的球心为，由求出半径，代入球的表面积公式即可.
【详解】
如图，分别取，的中点，，连接，.
因为是边长为4的等边三角形，
所以，
所以，
则四边形外接圆的圆心为，半径.
设四棱锥外接球的球心为，连接，过点作，垂足为.
易证四边形是矩形，则，.
设四棱锥外接球的半径为，
则，
即，解得，
故四棱锥外接球的表面积是.
故答案为：
题型三、折叠的综合性问题
例3、（2022·江苏扬州·高三期末）在边长为6的正三角形ABC中M，N分别为边AB，AC上的点，且满足，把△AMN沿着MN翻折至A′MN位置，则下列说法中正确的有（ ）
A．在翻折过程中，在边A′N上存在点P，满足CP∥平面A′BM
B．若，则在翻折过程中的某个位置，满足平面A′BC⊥平面BCNM
C．若且二面角A′－MN－B的大小为120°，则四棱锥A′－BCNM的外接球的表面积为61π
D．在翻折过程中，四棱锥A′－BCNM体积的最大值为
【答案】BCD
【分析】
通过直线相交来判断A选项的正确性；通过面面垂直的判定定理判断B选项的正确性；通过求四棱锥外接球的表面积来判断C选项的正确性；利用导数来求得四棱锥体积的最大值.
【详解】
对于选项A，过作，交于，则无论点P在A′N上什么位置，都存在CP与BQ相交，折叠后为梯形BCQP，
则CP不与平面A′BM平行，故选项A错误；
对于选项B，设分别是的中点，
若，则AE＞DE，所以存在某一位置使得A′D⊥DE，
又因为MN⊥A′E，MN⊥DE，且A′E∩DE＝E，所以MN⊥平面A′DE，所以MN⊥A′D，
，所以A′D⊥平面BCNM，所以A′BC⊥平面BCNM，故选项B正确；
对于选项C，设分别是的中点，
若且二面角A′－MN－B的大小为120°，则△AMN为正三角形，
∠BMN＝120°，∠C＝60°，则BCNM四点共圆，圆心可设为点G，其半径设为r，
DB＝DC＝DM＝DN＝3，所以点G即为点D，所以r＝3，
二面角A′－MN－B的平面角即为∠A′ED＝120°，过点A′作A′H⊥DE，垂足为点H，
EH＝，DH＝，A′H＝，，
设外接球球心为，由，解得R2＝，
所以外接球的表面积为S＝4πR2＝61π，故选项C正确；
对于选项D，设分别是的中点，设是四棱锥的高.
S△AMN＝6λ6λ＝9λ2，
S△ABC＝66＝9，
所以S四边形BCNM＝9（1－λ2），则VA′－BCNM＝9（1－λ2）h≤3（1－λ2）A′E
＝3（1－λ2）3λ＝27（－λ3＋λ），λ∈（0，1），
可设f（λ）＝27（－λ3＋λ），λ∈（0，1），
则＝27（－3λ2＋1），令＝0，
解得λ＝，则函数f（λ）在（0，）上单调递增，在（，1）上单调递减，
所以f（λ）max＝f（）＝6，
则四棱锥A′－BCN体积的最大值为，故选项D正确.
故选：BCD
变式1、（2021·山东滨州市·高三二模）已知正方形的边长为2，将沿AC翻折到的位置，得到四面体，在翻折过程中，点始终位于所在平面的同一侧，且的最小值为，则下列结论正确的是（ ）
A．四面体的外接球的表面积为
B．四面体体积的最大值为
C．点D的运动轨迹的长度为
D．边AD旋转所形成的曲面的面积为
【答案】ACD
【解析】
对ABCD各选项逐一分析即可求解.
【详解】
解：对A：，
AC中点即为四面体的外接球的球心，AC为球的直径，
，
，故选项A正确；
对B：当平面平面时，四面体体积的最大，此时高为，
，故选项B错误；
对C：设方形对角线AC与BD交于O，
由题意，翻折后当的最小值为时，为边长为的等边三角形，
此时，所以点D的运动轨迹是以O为圆心为半径的圆心角为的圆弧，
所以点D的运动轨迹的长度为，故选项C正确；
对D：结合C的分析知，边AD旋转所形成的曲面的面积为以A为顶点，
底面圆为以O为圆心为半径的圆锥的侧面积的，
即所求曲面的面积为，故选项D正确.
故选: ACD.
变式2、【2022·广东省深圳市宝安区第一次调研10月】如图甲是由正方形，等边和等边组成的一个平面图形，其中，将其沿，，折起得三棱锥，如图乙.
（1）求证：平面平面；
（2）过棱作平面交棱于点，且三棱锥和的体积比为，求直线与平面所成角的正弦值.
【答案】（1）证明见解析；（2）.
【解析】
【分析】（1）取的中点为，连接，，证明，，即证平面，即证得面面垂直；
（2）建立如图空间直角坐标系，写出对应点的坐标和向量的坐标，再计算平面法向量，利用所求角的正弦为即得结果.
【详解】（1）证明：如图，取的中点为，连接，.
∵，∴.
∵，，
∴，同理.
又，∴，
∴.∵，，平面，
∴平面.
又平面，
∴平面平面；
（2）解：如图建立空间直角坐标系，根据边长关系可知，，，，，∴，.
∵三棱锥和的体积比为，
∴，∴，∴.
设平面的法向量为，则，令，得.
设直线与平面所成角为，则.
∴直线与平面所成角的正弦值为.