高考数学第一轮复习讲练测(新教材新高考)专题3.5指数与指数函数(练)原卷版+解析

这是一份高考数学第一轮复习讲练测(新教材新高考)专题3.5指数与指数函数(练)原卷版+解析，共24页。试卷主要包含了【多选题】等内容，欢迎下载使用。

1．（2021·山东）设全集，集合，，则（ ）
A．B．C．D．
2.（2019·贵州省织金县第二中学高一期中）函数且过定点（ ）
A．B．C．D．
3．（2021·江西高三二模（文））下列函数中，在上单调递增的是（ ）
A．B．C．D．
4．（2020·浙江高三月考）当时，“函数的值恒小于1”的一个充分不必要条件是（ ）
A．B．C．D．
5．（2019·浙江高三专题练习）已知函数（其中的图象如图所示，则函数的图象是（ ）
A．B．
C．D．
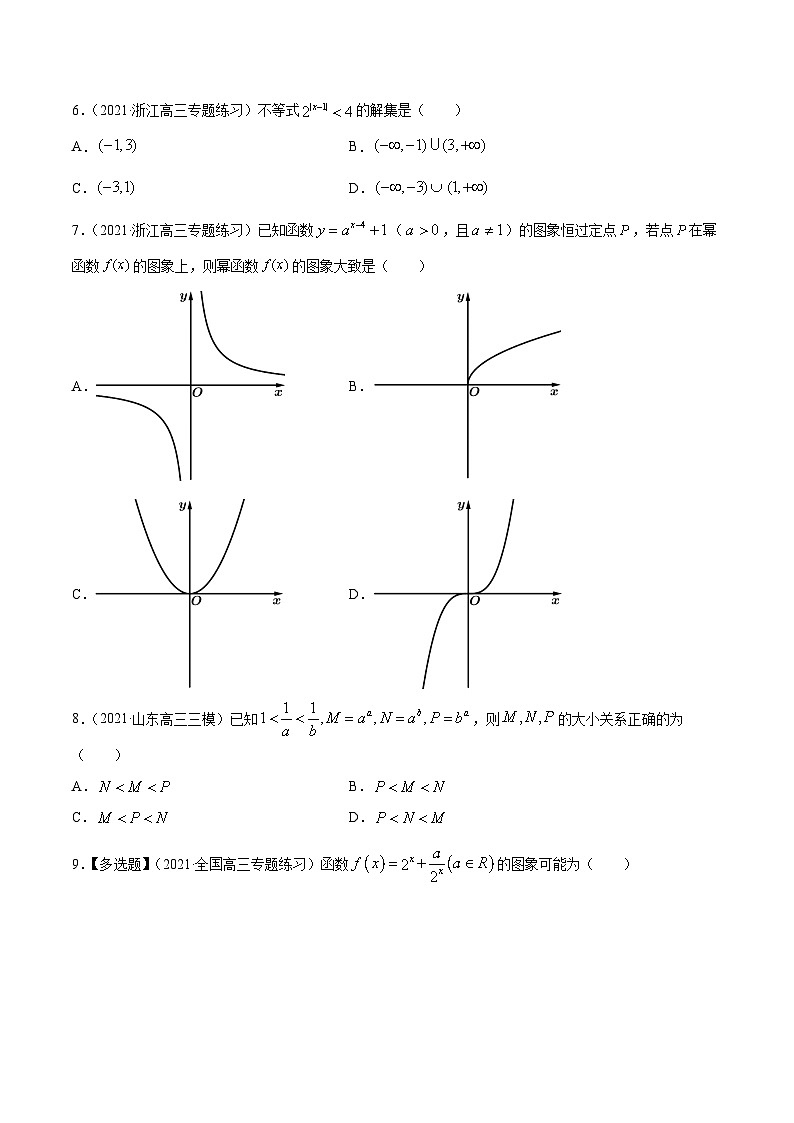
6．（2021·浙江高三专题练习）不等式的解集是（ ）
A．B．
C．D．
7．（2021·浙江高三专题练习）已知函数（，且）的图象恒过定点，若点在幂函数的图象上，则幂函数的图象大致是（ ）
A．B．
C．D．
8．（2021·山东高三三模）已知，则的大小关系正确的为（ ）
A．B．
C．D．
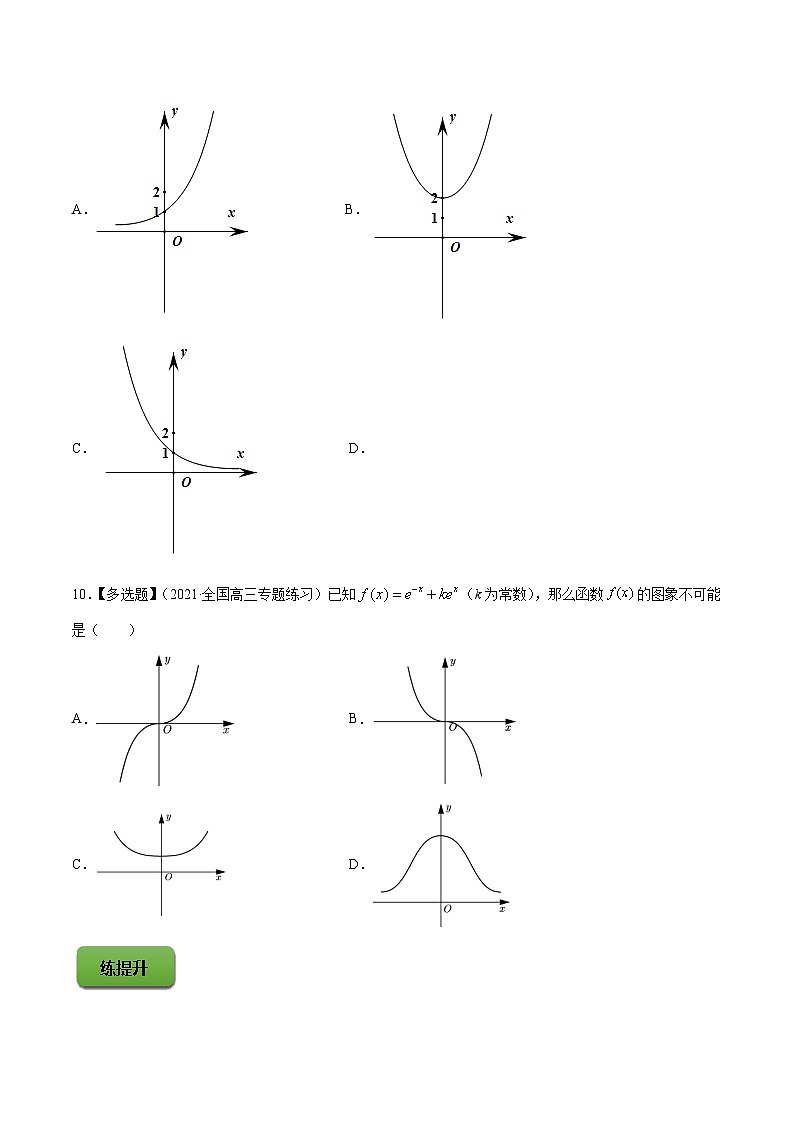
9．【多选题】（2021·全国高三专题练习）函数的图象可能为（ ）
A． B．
C．D．
10．【多选题】（2021·全国高三专题练习）已知（k为常数），那么函数的图象不可能是（ ）
A．B．
C．D．
练提升TIDHNEG
1．（2021·浙江金华市·高三其他模拟）已知函数，若对于任意一个正数，不等式在上都有解，则的取值范围是（ ）
A．B．
C．D．
2．（2021·安徽芜湖市·高三二模（理））函数是定义在上的偶函数，且当时，.若对任意的，均有，则实数的最大值是（ ）
A．B．C．0D．
3．（2021·辽宁沈阳市·高三三模）已知，则的大小关系为（ ）
A．B．C．D．
4．（2021·江苏苏州市·高三其他模拟）生物体死亡后，它机体内原有的碳14含量P会按确定的比率衰减(称为衰减率)，P与死亡年数t之间的函数关系式为(其中a为常数)，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”.若2021年某遗址文物出土时碳14的残余量约占原始含量的79%，则可推断该文物属于（ ）参考数据：.
参考时间轴：
A．战国B．汉C．唐D．宋
5．（2021·河南高三月考（理））设实数，满足，，则，的大小关系为（ ）
A．B．C．D．无法比较
6．【多选题】（2021·全国高三专题练习）若函数，则下述正确的有（ ）
A． 在R上单调递增B．的值域为
C． 的图象关于点对称D． 的图象关于直线对称
7．【多选题】（2020·山东省青岛第十六中学高三月考）已知函数，则下列正确的是（ ）
A．B．
C．D．的值域为
8．【多选题】（2020·河北冀州中学（衡水市冀州区第一中学）高三月考）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设，用表示不超过的最大整数，则称为高斯函数，例如：，.已知函数，则关于函数的叙述中正确的是（ ）
A．是偶函数B．是奇函数
C．在上是增函数D．的值域是
9．【多选题】（2020·重庆市第十一中学校高三月考）已知函数（为常数），函数的最小值为，则实数的取值可以是（ ）
A．-1B．2C．1D．0
10．【多选题】（2021·南京市中华中学高三期末）“悬链线”进入公众视野，源于达芬奇的画作《抱银貂的女人》.这幅画作中，女士脖颈上悬挂的黑色珍珠链与主人相互映衬，显现出不一样的美与光泽.而达芬奇却心生好奇：“固定项链的两端，使其在重力作用下自然下垂，那么项链所形成的曲线是什么？”随着后人研究的深入，悬链线的庐山真面目被揭开.法国著名昆虫学家、文学家法布尔，在《昆虫记》里有这样的记载：“每当地心引力和扰性同时发生作用时，悬链线就在现实中出现了.当一条悬链弯曲成两点不在同一垂直线（注：垂直于地面的直线）上的曲线时，人们便把这曲线称为悬链线.这就是一条软绳子两端抓住而垂下来的形状，这就是一张被风鼓起来的船帆外形的那条线条．”建立适当的平面直角坐标系，可以写出悬链线的函数解析式：，其中为悬链线系数．当时，称为双曲余弦函数，记为．类似的双曲正弦函数．直线与和的图像分别交于点、．下列结论正确的是（ ）
A．B．
C．随的增大而减小D．与的图像有完全相同的渐近线
练真题TIDHNEG
1.(新课标真题)已知集合A={x|x<1}，B={x|}，则（ ）
A．B．
C．D．
2．（2020·北京高考真题）已知函数，则不等式的解集是（ ）．
A．B．
C．D．
3.(北京高考真题)已知函数，则（ ）
（A）是偶函数，且在R上是增函数
（B）是奇函数，且在R上是增函数
（C）是偶函数，且在R上是减函数
（D）是奇函数，且在R上是增函数
4.(2019年高考北京理)设函数（a为常数）．若f（x）为奇函数，则a=________；若f（x）是R上的增函数，则a的取值范围是___________．
5.（山东高考真题）已知f(x)是定义在R上的偶函数，且f(x＋4)＝f(x－2)．若当x∈[－3,0]时，f(x)＝6－x，则f(919)＝________.
6.（2019·全国高考真题（理））已知是奇函数，且当时，.若，则__________.
专题3.5 指数与指数函数
练基础
1．（2021·山东）设全集，集合，，则（ ）
A．B．C．D．
【答案】B
【解析】
利用指数函数的性质求解集合B，再求集合的补集，交集即可.
【详解】
由题知，
又，则，
故选：B.
2.（2019·贵州省织金县第二中学高一期中）函数且过定点（ ）
A．B．C．D．
【答案】D
【解析】
令，所以函数且过定点．
3．（2021·江西高三二模（文））下列函数中，在上单调递增的是（ ）
A．B．C．D．
【答案】C
【解析】
利用二次函数的性质判定A；利用分段函数的图象可以判定B；根据幂函数和对数函数的性质判定C,D．
【详解】
A中，的图象关于轴对称，开口向下的抛物线，在上单调递减，故Ａ不对；
B中，的图像关于直线对称，在上单调递减，在上单调递增，故排除B；
C中，由幂函数的性质可知在上单调递增，故C正确；
D中，根据指数函数的性质可得在上单调递减，故排除D；
故选：C．
4．（2020·浙江高三月考）当时，“函数的值恒小于1”的一个充分不必要条件是（ ）
A．B．C．D．
【答案】D
【解析】
由指数函数的图象与性质可得原命题等价于，再由充分不必要条件的概念即可得解.
【详解】
若当时，函数的值恒小于1，则即，
所以当时，函数的值恒小于1的一个充分不必要条件是.
故选：D.
5．（2019·浙江高三专题练习）已知函数（其中的图象如图所示，则函数的图象是（ ）
A．B．
C．D．
【答案】C
【解析】
由二次函数的图象确定的取值范围，然后可确定的图象．
【详解】
由函数的图象可知，，，则为增函数，，过定点，
故选：.
6．（2021·浙江高三专题练习）不等式的解集是（ ）
A．B．
C．D．
【答案】A
【解析】
根据题意得，再解绝对值不等式即可得答案.
【详解】
解：由指数函数在上单调递增，，
所以，进而得，即.
故选：A.
7．（2021·浙江高三专题练习）已知函数（，且）的图象恒过定点，若点在幂函数的图象上，则幂函数的图象大致是（ ）
A．B．
C．D．
【答案】B
【解析】
由指数函数性质求得定点坐标，由定点求得幂函数解析式，确定图象．
【详解】
由得，，即定点为，
设，则，，所以，图象为B．
故选：B．
8．（2021·山东高三三模）已知，则的大小关系正确的为（ ）
A．B．
C．D．
【答案】B
【解析】
根据指数函数与幂函数的单调性即可求解.
【详解】
解：，
，
指数函数在上单调递减，
，即，
又幂函数在上单调递增，
，即，
，
故选：B.
9．【多选题】（2021·全国高三专题练习）函数的图象可能为（ ）
A． B．
C．D．
【答案】ABD
【解析】
根据函数解析式的形式，以及图象的特征，合理给赋值，判断选项.
【详解】
当时，，图象A满足；
当时，，，且，此时函数是偶函数，关于轴对称，图象B满足；
当时，，，且，此时函数是奇函数，关于原点对称，图象D满足；
图象C过点，此时，故C不成立.
故选：ABD
10．【多选题】（2021·全国高三专题练习）已知（k为常数），那么函数的图象不可能是（ ）
A．B．
C．D．
【答案】AD
【解析】
根据选项，四个图象可知备选函数都具有奇偶性．当时，为偶函数，当时，为奇函数，再根据单调性进行分析得出答案．
【详解】
由选项的四个图象可知，备选函数都具有奇偶性．
当时，为偶函数，
当时，且单调递增，而在上单调递增，
故函数在上单调递增，故选项C正确，D错误；
当时，为奇函数，
当时，且单调递增，而在上单调递减，
故函数在上单调递减，故选项B正确，A错误.
故选:AD．
练提升TIDHNEG
1．（2021·浙江金华市·高三其他模拟）已知函数，若对于任意一个正数，不等式在上都有解，则的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】
由不等式可知，或，结合图象，分析可得的取值范围.
【详解】
当时，，得，，不能满足都有解；
当时，，得或，
如图，当或时，只需满足或，满足条件.
所以，时，满足条件.
故选：A
2．（2021·安徽芜湖市·高三二模（理））函数是定义在上的偶函数，且当时，.若对任意的，均有，则实数的最大值是（ ）
A．B．C．0D．
【答案】A
【解析】
首先根据函数是偶函数，求出函数的解析式，结合不等式的关系进行转化，利用单调性转化为不等式恒成立问题即可求解.
【详解】
∵是定义在上的偶函数，且当时，，
∴，当时为增函数，
∴，
则等价于，
即，即对任意恒成立，
设，
则有，解得，
又∵，∴.
故选：A.
3．（2021·辽宁沈阳市·高三三模）已知，则的大小关系为（ ）
A．B．C．D．
【答案】B
【解析】
根据指数函数的单调性，将问题转化为比较当时的大小，利用特值法即可求得结果.
【详解】
因为，函数是单调增函数，
所以比较a，b，c的大小，只需比较当时的大小即可.
用特殊值法，取，容易知，
再对其均平方得，
显然，
所以，所以
故选：B.
4．（2021·江苏苏州市·高三其他模拟）生物体死亡后，它机体内原有的碳14含量P会按确定的比率衰减(称为衰减率)，P与死亡年数t之间的函数关系式为(其中a为常数)，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”.若2021年某遗址文物出土时碳14的残余量约占原始含量的79%，则可推断该文物属于（ ）参考数据：.
参考时间轴：
A．战国B．汉C．唐D．宋
【答案】B
【解析】
根据“半衰期”得，进而解方程得，进而可推算其所处朝代.
【详解】
由题可知，当时，，故，解得，
所以，所以当时，解方程，
两边取以为底的对数得，解得，
所以，
所以可推断该文物属于汉朝.
故选：B
5．（2021·河南高三月考（理））设实数，满足，，则，的大小关系为（ ）
A．B．C．D．无法比较
【答案】A
【解析】
从选项A或C出发，分析其对立面，推理导出矛盾结果或成立的结果即可得解.
【详解】
假设，则，，
由得，
因函数在上单调递减，又，则，所以；
由得，
因函数在上单调递减，又，则，所以；
即有与假设矛盾，所以，
故选：A
6．【多选题】（2021·全国高三专题练习）若函数，则下述正确的有（ ）
A． 在R上单调递增B．的值域为
C． 的图象关于点对称D． 的图象关于直线对称
【答案】AC
【解析】
A.由和的单调性判断；B.取判断；C.D.判断是否等于零即可.
【详解】
因为是定义在R上的增函数，是定义在R上的减函数，
所以在R上单调递增，故A正确；
因为，故B错误；
因为，
所以的图象关于点对称，故C正确，D错误．
故选：AC．
7．【多选题】（2020·山东省青岛第十六中学高三月考）已知函数，则下列正确的是（ ）
A．B．
C．D．的值域为
【答案】BD
【解析】
对选项A，根据计算，即可判断A错误，对选项B，根据计算，即可判断B正确；对选项C，根据计算，即可判断C错误，对选项D，分别求和的值域即可得到答案.
【详解】
对选项A，，，
故A错误；
对选项B，，，
故B正确.
对选项C，因为，所以，
，故C错误；
对选项D，当时，，函数的值域为，
当时，，，
函数的值域为，
又因为时，，是周期为的函数，
所以当时，函数的值域为，
综上，函数的值域为，故D正确.
故选：BD
8．【多选题】（2020·河北冀州中学（衡水市冀州区第一中学）高三月考）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设，用表示不超过的最大整数，则称为高斯函数，例如：，.已知函数，则关于函数的叙述中正确的是（ ）
A．是偶函数B．是奇函数
C．在上是增函数D．的值域是
【答案】BC
【解析】
由判断A；由奇函数的定义证明B；把的解析式变形，由的单调性结合复合函数的单调性判断C正确；求出的范围，进一步求得的值域判断D．
【详解】
，，
，则不是偶函数，故A错误；
的定义域为，
，
为奇函数，故B正确；
，
又在上单调递增，在上是增函数，故C正确；
，，则，可得，
即．
，故D错误．
故选：BC．
9．【多选题】（2020·重庆市第十一中学校高三月考）已知函数（为常数），函数的最小值为，则实数的取值可以是（ ）
A．-1B．2C．1D．0
【答案】CD
【解析】
由已知求得当时，的最小值为，问题转化为当时，恒成立，对分类讨论求得的范围，结合选项得答案．
【详解】
当时，单调递减，且当时，函数取得最小值为；
要使原分段函数有最小值为，
则当时，恒成立，
当时，满足；
当时，需，即．
综上，实数的取值范围为．
结合选项可得，实数的取值可以是1，0．
故选：CD．
10．【多选题】（2021·南京市中华中学高三期末）“悬链线”进入公众视野，源于达芬奇的画作《抱银貂的女人》.这幅画作中，女士脖颈上悬挂的黑色珍珠链与主人相互映衬，显现出不一样的美与光泽.而达芬奇却心生好奇：“固定项链的两端，使其在重力作用下自然下垂，那么项链所形成的曲线是什么？”随着后人研究的深入，悬链线的庐山真面目被揭开.法国著名昆虫学家、文学家法布尔，在《昆虫记》里有这样的记载：“每当地心引力和扰性同时发生作用时，悬链线就在现实中出现了.当一条悬链弯曲成两点不在同一垂直线（注：垂直于地面的直线）上的曲线时，人们便把这曲线称为悬链线.这就是一条软绳子两端抓住而垂下来的形状，这就是一张被风鼓起来的船帆外形的那条线条．”建立适当的平面直角坐标系，可以写出悬链线的函数解析式：，其中为悬链线系数．当时，称为双曲余弦函数，记为．类似的双曲正弦函数．直线与和的图像分别交于点、．下列结论正确的是（ ）
A．B．
C．随的增大而减小D．与的图像有完全相同的渐近线
【答案】AC
【解析】
由函数的定义，代入化简可得A正确，B不正确；由可得C正确；由函数的图象变化可得D不正确.
【详解】
，所以A正确；
，所以B不正确；
，且随着变大，越来越小，所以C正确；
，当时，是的等价无穷大，无渐近线，
，当时，是的等价无穷大，无渐近线，所以D不正确.
故选：AC
练真题TIDHNEG
1.(新课标真题)已知集合A={x|x<1}，B={x|}，则（ ）
A．B．
C．D．
【答案】A
【解析】
由可得，则，即，所以
，，故选A.
2．（2020·北京高考真题）已知函数，则不等式的解集是（ ）．
A．B．
C．D．
【答案】D
【解析】
因为，所以等价于，
在同一直角坐标系中作出和的图象如图：
两函数图象的交点坐标为，
不等式的解为或.
所以不等式的解集为：.
故选：D.
3.(北京高考真题)已知函数，则（ ）
（A）是偶函数，且在R上是增函数
（B）是奇函数，且在R上是增函数
（C）是偶函数，且在R上是减函数
（D）是奇函数，且在R上是增函数
【答案】B
【解析】
4.(2019年高考北京理)设函数（a为常数）．若f（x）为奇函数，则a=________；若f（x）是R上的增函数，则a的取值范围是___________．
【答案】
【解析】首先由奇函数的定义得到关于的恒等式，据此可得的值，然后利用可得a的取值范围.
若函数为奇函数，则即，
即对任意的恒成立，
则，得.
若函数是R上的增函数，则在R上恒成立，
即在R上恒成立，
又，则，
即实数的取值范围是.
5.（山东高考真题）已知f(x)是定义在R上的偶函数，且f(x＋4)＝f(x－2)．若当x∈[－3,0]时，f(x)＝6－x，则f(919)＝________.
【答案】6
【解析】
由f(x+4)=f(x-2)可知,fx是周期函数,且T=6,所以f(919)=f(6×653+1)=f(1) =f(−1)=6.
6.（2019·全国高考真题（理））已知是奇函数，且当时，.若，则__________.
【答案】-3
【解析】
因为是奇函数，且当时，．
又因为，，
所以，两边取以为底的对数得，所以，即．