
所属成套资源:高考数学一轮复习(新教材新高考)专项练习(学生版+解析)
高考数学一轮复习(新教材新高考)第01讲函数及其性质(单调性、奇偶性、周期性、对称性)专项练习(学生版+解析)
展开
这是一份高考数学一轮复习(新教材新高考)第01讲函数及其性质(单调性、奇偶性、周期性、对称性)专项练习(学生版+解析),共87页。试卷主要包含了 4年真题考点分布, 命题规律及备考策略,了解周期性的概念和意义等内容,欢迎下载使用。
(核心考点精讲精练)
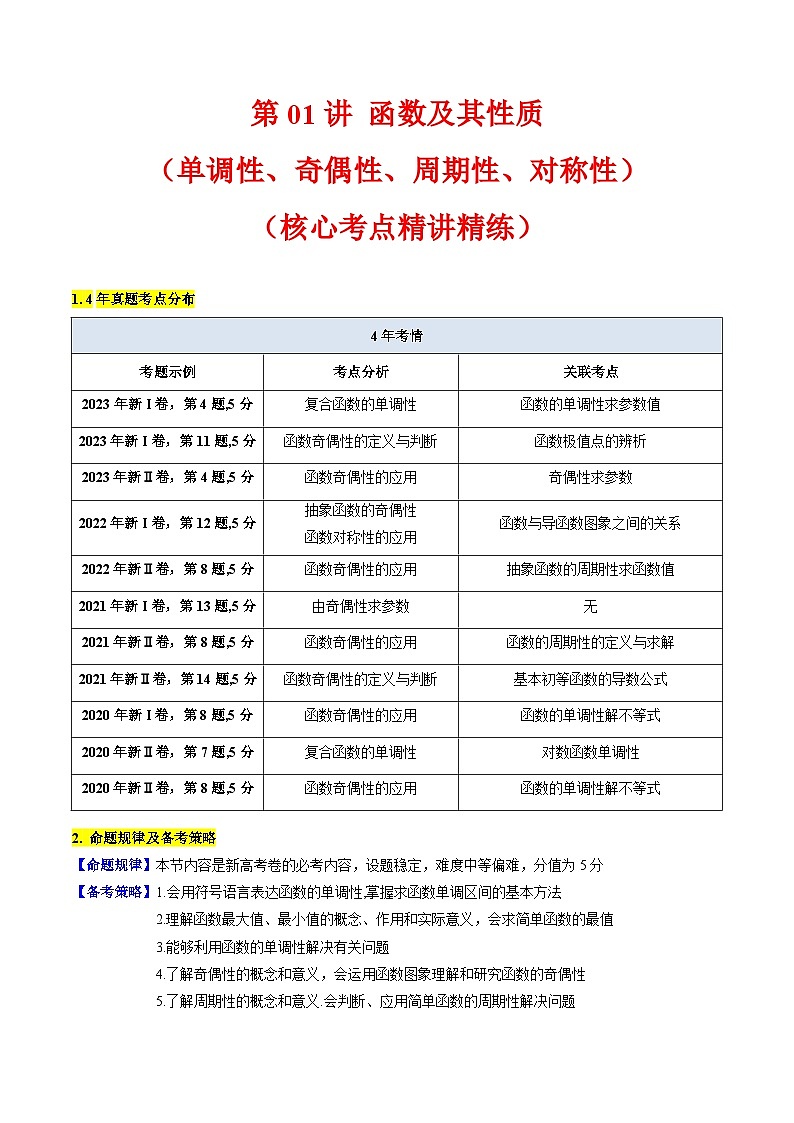
1. 4年真题考点分布
2. 命题规律及备考策略
【命题规律】本节内容是新高考卷的必考内容,设题稳定,难度中等偏难,分值为5分
【备考策略】1.会用符号语言表达函数的单调性,掌握求函数单调区间的基本方法
2.理解函数最大值、最小值的概念、作用和实际意义,会求简单函数的最值
3.能够利用函数的单调性解决有关问题
4.了解奇偶性的概念和意义,会运用函数图象理解和研究函数的奇偶性
5.了解周期性的概念和意义.会判断、应用简单函数的周期性解决问题
6.能综合运用函数的奇偶性、单调性、周期性、对称性等解决相关问题.
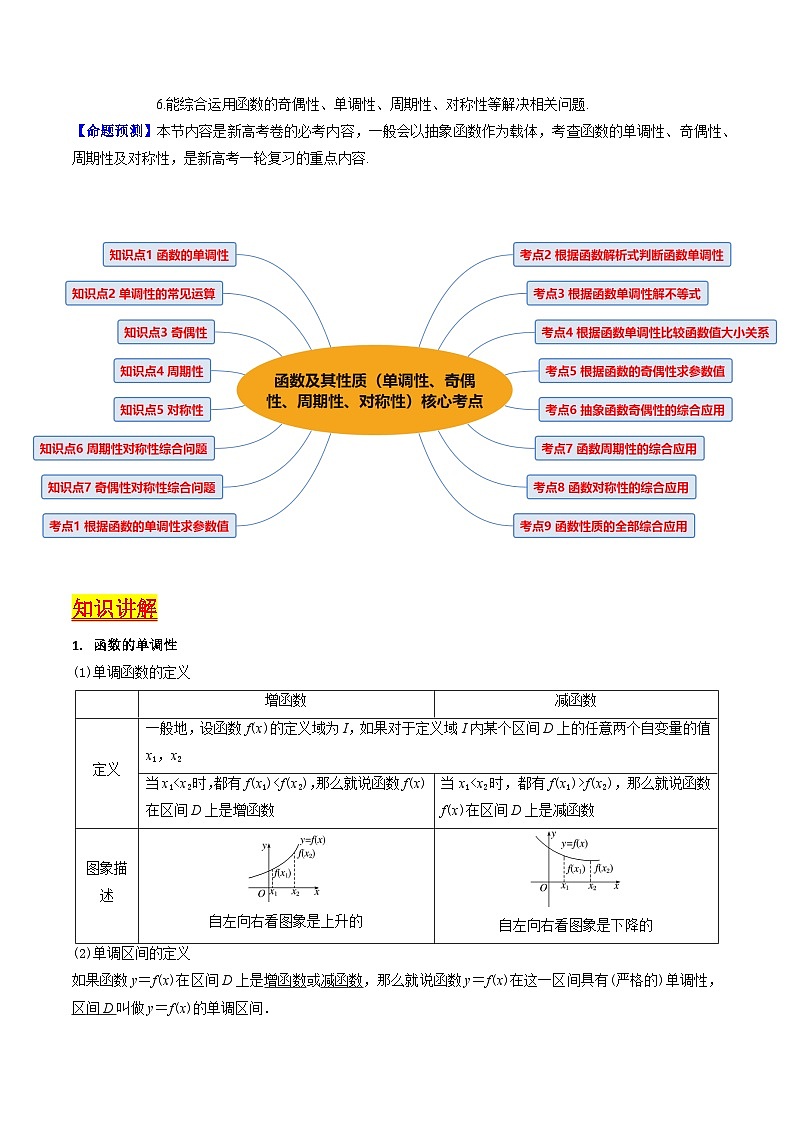
【命题预测】本节内容是新高考卷的必考内容,一般会以抽象函数作为载体,考查函数的单调性、奇偶性、周期性及对称性,是新高考一轮复习的重点内容.
知识讲解
函数的单调性
(1)单调函数的定义
(2)单调区间的定义
如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
(3)函数的最值
单调性的常见运算
单调性的运算
①增函数(↗)增函数(↗)增函数↗
②减函数(↘)减函数(↘)减函数↘
③为↗,则为↘,为↘
④增函数(↗)减函数(↘)增函数↗
⑤减函数(↘)增函数(↗)减函数↘
⑥增函数(↗)减函数(↘)未知(导数)
复合函数的单调性
奇偶性
①具有奇偶性的函数定义域关于原点对称(大前提)
②奇偶性的定义:
奇函数:,图象关于原点对称
偶函数:,图象关于轴对称
③奇偶性的运算
周期性(差为常数有周期)
①若,则的周期为:
②若,则的周期为:
③若,则的周期为:(周期扩倍问题)
④若,则的周期为:(周期扩倍问题)
对称性(和为常数有对称轴)
轴对称
①若,则的对称轴为
②若,则的对称轴为
点对称
①若,则的对称中心为
②若,则的对称中心为
周期性对称性综合问题
①若,,其中,则的周期为:
②若,,其中,则的周期为:
③若,,其中,则的周期为:
奇偶性对称性综合问题
①已知为偶函数,为奇函数,则的周期为:
②已知为奇函数,为偶函数,则的周期为:
考点一、根据函数的单调性求参数值
1.(2023年新高考全国Ⅰ卷数学真题)设函数在区间上单调递减,则的取值范围是( )
A.B.
C.D.
【答案】D
【分析】利用指数型复合函数单调性,判断列式计算作答.
【详解】函数在R上单调递增,而函数在区间上单调递减,
则有函数在区间上单调递减,因此,解得,
所以的取值范围是.
故选:D
2.(2023·全国·高三专题练习)若函数在区间上单调递减,则a的取值范围是______.
【答案】
【分析】按值对函数 进行分类讨论,再结合函数 的性质求解作答.
【详解】由于函数在区间上单调递减,
①当时,函数,在区间上单调递减,符合题意;
②当时,开口向下,对称轴为,则,可得函数在区间上单调递减,符合题意;
③当时,开口向上,对称轴为,在区间上单调递减需满足,因此.
综上所述,a的取值范围是.
故答案为:
1.(2023·全国·高三专题练习)函数在上单调递增,则实数的取值范围是________.
【答案】.
【分析】先求得的单调递增区间为,根据题意得到,即可求解.
【详解】由函数,可得函数的单调递增区间为,
因为在上单调递增,可得,解得,
所以实数的取值范围为.
故答案为:.
2.(2023·全国·高三专题练习)若函数在上单调递增,则实数的取值范围为________.
【答案】
【分析】化简,根据题意得到,即可求解.
【详解】由函数,
因为在上单调递增,则满足,解得,
所以实数的取值范围为.
故答案为:.
3.(2023·全国·高三专题练习)函数在上单调递增,则实数的取值范围是________.
【答案】
【分析】先利用反比例函数的单调性得到在与上单调递减,再利用参数分离法得到,从而得到关于的不等式组,解之即可.
【详解】因为在与上单调递减,
而在上单调递增,
所以,解得或,
所以的取值范围是.
故答案为:
考点二、根据函数解析式判断函数单调性
1.(2023·北京·统考高考真题)下列函数中,在区间上单调递增的是( )
A.B.
C.D.
【答案】C
【分析】利用基本初等函数的单调性,结合复合函数的单调性判断ABC,举反例排除D即可.
【详解】对于A,因为在上单调递增,在上单调递减,
所以在上单调递减,故A错误;
对于B,因为在上单调递增,在上单调递减,
所以在上单调递减,故B错误;
对于C,因为在上单调递减,在上单调递减,
所以在上单调递增,故C正确;
对于D,因为,,
显然在上不单调,D错误.
故选:C.
2.(2021·全国·高考真题)下列函数中是增函数的为( )
A.B.C.D.
【答案】D
【分析】根据基本初等函数的性质逐项判断后可得正确的选项.
【详解】对于A,为上的减函数,不合题意,舍.
对于B,为上的减函数,不合题意,舍.
对于C,在为减函数,不合题意,舍.
对于D,为上的增函数,符合题意,
故选:D.
1.(2023·浙江·统考二模)下列函数在区间上单调递增的是( )
A.B.
C.D.
【答案】D
【分析】对于BCD,根据各个选项观察均是向右平移两个单位长度的形式,根据原函数的单调区间可以判断平移后的单调区间,进而判断上的单调性得到结论,而根据二次函数的单调性可判断A的正误.
【详解】对于选项:开口向上,对称轴,所以在上单调递减,故不符合题意.
对于选项:是向右平移了两个单位长度,所以在在上单调递减,故不符合题意.
对于选项:是向右平移了两个单位长度,
所以在上单调递减,在上单调递增,
因为,所以不符合题意.
对于选项:是向右平移了两个单位长度,
所以在上单调递增,则在上单调递增,符合题意.
故选.
2.(2023·北京海淀·校考三模)下列函数中,在区间上是减函数的是( )
A.B.C.D.
【答案】D
【分析】根据基本初等函数的单调性及对数型复合函数的单调性判断即可.
【详解】对于A:在定义域上单调递增,故A错误;
对于B:在定义域上单调递增,故B错误;
对于C:定义域为,因为在上单调递减且值域为,
又在定义域上单调递减,所以在上单调递增,故C错误;
对于D:,函数在上单调递减,故D正确;
故选:D
3.(2023·吉林·统考二模)下列四个函数中,在其定义域内单调递增的是( )
A.B.C.D.
【答案】A
【分析】根据幂函数单调性即可判断出A正确,C错误,再根据正切函数和指数函数图象即可得出BD错误.
【详解】由幂函数性质可知,定义域为,且在定义域内单调递增;即A正确;
在其定义域,上分别单调递减,即C错误;
由正切函数图像可知,为周期函数,在定义域内不是单调递增,B错误;
由指数函数性质可知,在上为单调递减,所以D错误.
故选:A
考点三、根据函数单调性解不等式
1.(2023·全国·高三专题练习)已知函数,若f(a-2)>3,则a的取值范围是________.
【答案】(0,1)
【分析】利用函数的单调性解不等式.
【详解】解:因为在R上递减,在(-2,+∞)上递增,
所以在定义域(-2,+∞)上是减函数,且f(-1)=3,
由f(a-2)>3,得f(a-2)>f(-1),
∴,
解得0
相关试卷
这是一份高考数学第一轮复习(新教材新高考)第01讲函数及其性质(单调性、奇偶性、周期性、对称性)(核心考点精讲精练)(学生版+解析),共87页。试卷主要包含了 4年真题考点分布, 命题规律及备考策略,了解周期性的概念和意义等内容,欢迎下载使用。
这是一份高考数学一轮复习讲练测(新教材新高考)第02讲函数的性质:单调性、奇偶性、周期性、对称性(练习)(原卷版+解析),共26页。
这是一份第01讲 函数及其性质(单调性、奇偶性、周期性、对称性)(12类核心考点精讲精练)-备战2025年高考数学一轮复习考点帮(新高考通用),文件包含第01讲函数及其性质单调性奇偶性周期性对称性教师版docx、第01讲函数及其性质单调性奇偶性周期性对称性学生版docx等2份试卷配套教学资源,其中试卷共83页, 欢迎下载使用。









