




所属成套资源:2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版)全套课件
- 第01讲 集合(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第03讲 等式性质与不等式性质(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第04讲 基本不等式(考点串讲PPT)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第05讲 一元二次方程、不等式(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第06讲 函数的概念及其表示(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
第02讲 常用逻辑用语(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点
展开
这是一份第02讲 常用逻辑用语(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点,共48页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,充分不必要,必要不充分,既不充分也不必要,∀x∈Mpx,∃x∈Mpx等内容,欢迎下载使用。
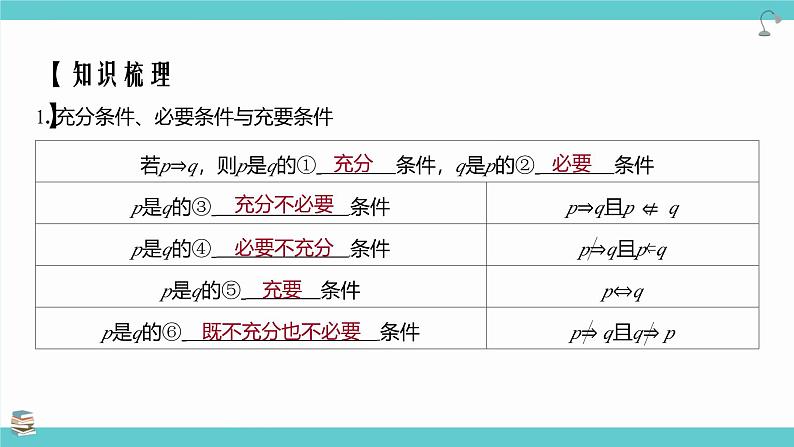
1. 充分条件、必要条件与充要条件
2. 全称量词与存在量词(1)全称量词与存在量词
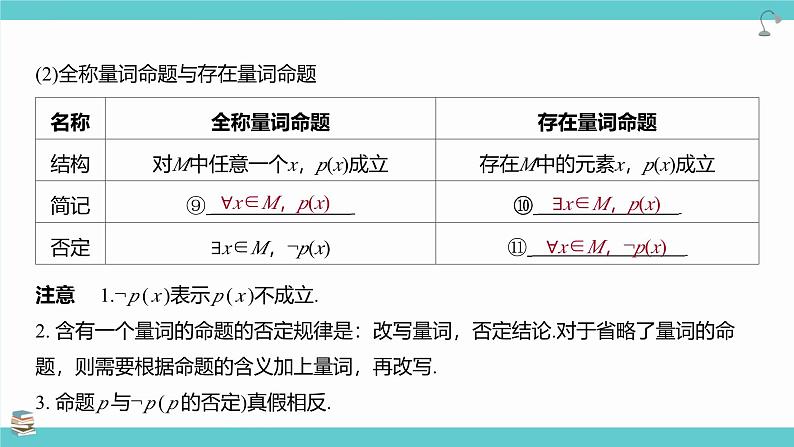
(2)全称量词命题与存在量词命题
注意 1.¬ p ( x )表示 p ( x )不成立.2. 含有一个量词的命题的否定规律是:改写量词,否定结论.对于省略了量词的命
题,则需要根据命题的含义加上量词,再改写.3. 命题 p 与¬ p ( p 的否定)真假相反.
∀x∈M,¬p(x)
充分、必要条件与对应集合之间的关系设 A ={ x | p ( x )}, B ={ x | q ( x )}.(1)若 p 是 q 的充分条件,则 A ⊆ B ;若 p 是 q 的必要条件,则 A ⊇ B . (2)若 p 是 q 的充分不必要条件,则 A ⫋ B ;若 p 是 q 的必要不充分条件,则 A ⫌ B . (3)若 p 是 q 的充要条件,则 A = B .
易错点1 条件判定不全面而致误
易错点2 不能正确区分命题的条件与结论而致误
易错点3 不能正确理解全称量词与存在量词的概念而致错
易错点4 忽视否定的范围而致错
∃a,b∈R,方程ax2+b=0无解或至少有两解
命题点1 充分条件与必要条件
角度1 充分条件与必要条件的判断例1 (1)[2023天津高考]“ a 2= b 2”是“ a 2+ b 2=2 ab ”的( B )
[解析] 因为“ a 2= b 2”⇔“ a =- b 或 a = b ”, “ a 2+ b 2=2 ab ”⇔“ a = b ”,所以本题可以转化为判断“ a =- b 或 a = b ”与“ a = b ”的关系,又“ a =- b 或 a = b ”是“ a = b ”的必要不充分条件,所以“ a 2= b 2”是“ a 2+ b 2=2 ab ”的必要不充分条件.故选B.
(2)[2023全国卷甲]设甲: sin 2α+ sin 2β=1,乙: sin α+ cs β=0,则( B )
[解析] 甲等价于 sin 2α=1- sin 2β= cs 2β,等价于 sin α=± cs β,所以由甲不能
推导出 sin α+ cs β=0,所以甲不是乙的充分条件;由 sin α+ cs β=0,得 sin α=
- cs β,两边同时平方可得 sin 2α= cs 2β=1- sin 2β,即 sin 2α+ sin 2β=1,所以
由乙可以推导出甲,则甲是乙的必要条件.综上,选B.
A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件
A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
解得 m ≥9,所以实数 m 的取值范围为[9,+∞).
命题点2 全称量词与存在量词
角度1 全称量词命题和存在量词命题的否定及真假判断例3 (1)[2023辽宁名校联考]已知命题 p :∃ x <-1,2 x - x -1<0,则¬ p 为( B )
[解析] 因为命题 p :∃ x <-1,2 x - x -1<0,则¬ p :∀ x <-1,2 x - x -1≥0.故
选B.
(2)[2023湖北模拟]下列命题为真命题的是( C )
(2)[2024江苏南通学业质量监测]设命题 p :∃ x ∈R, ax 2- x +1≤0.写出一个实数 a
= ,使得 p 为真命题.
突破双变量“存在性”或“任意性”问题
角度2 双变量“存在性”或“任意性”的不等式问题
2.[2024湖北部分重点中学联考]设 m ∈R, a =( m ,1), b =(4, m ), c =
(1,-2),则 b ⊥ c 是 a ∥ b 的( A )
[解析] 若 b ⊥ c ,则4-2 m =0,得 m =2,即 b ⊥ c ⇔ m =2;若 a ∥ b ,则 m 2=
4,得 m =±2,即 a ∥ b ⇔ m =±2.因为 m =2是 m =±2的充分不必要条件,所以 b
⊥ c 是 a ∥ b 的充分不必要条件,故选A.
3. [2024福建南平模拟]若命题 p :∃ x >0, x 2-3 x +2>0,则命题 p 的否定为
( C )
[解析] 命题 p :∃ x >0, x 2-3 x +2>0是存在量词命题,其否定是全称量词命
题,所以命题 p 的否定为∀ x >0, x 2-3 x +2≤0.故选C.
4. [2024河南名校联考]若直线 l : Ax + By + C =0的倾斜角为α,则“α不是钝角”
是“ A · B <0”的( B )
5. [2024长春市质量监测(一)]“ a > b >1”是“lg a 2<lg b 2”的( A )
6. [2024江苏镇江模拟]命题“∀ x ∈[0,3], x 2-2 x - a ≤0”为真命题的一个充分不
必要条件是( A )
[解析] 由∀ x ∈[0,3], x 2-2 x - a ≤0,得 a ≥ x 2-2 x 在 x ∈[0,3]恒成立. y = x 2
-2 x 的图象开口向上,对称轴为直线 x =1,则其在[0,3]上的最大值为32-2×3=
3,则 a ≥3,结合选项可知, a ≥3的充分不必要条件为 a ≥4,故选A.
7. [2024山东聊城模拟]若存在 x ∈(0,2],使不等式 ax 2-2 x +3 a <0成立,则实数 a
的取值范围是( A )
9. [2024江西分宜中学、临川一中等校联考]已知{ an }是等比数列,则“ a 2< a 1<
0”是“{ an }为递减数列”的( A )
10. [2024湖南模拟]已知“ a ≤ x ≤ a 2+1”是“-2≤ x ≤5”的充分不必要条件,则
实数 a 的取值范围是( C )
11. [多选/2024江苏省高邮一中模拟]若“∀ x ∈ M ,| x |> x ”为真命题,
“∃ x ∈ M , x >3”为假命题,则集合 M 可以是( AB )
[解析] “∀ x ∈ M ,| x |> x ”为真命题,则 x <0,“∃ x ∈ M , x >3”为假命
题,则“∀ x ∈ M , x ≤3”为真命题.因此集合 M 的元素均为负数,故选AB.
12.[多选/2024重庆市合川区模拟]已知命题 p :∃ x ∈R, x 2+1<2 x ;命题 q :若 mx 2
- mx -1≠0恒成立,则-4< m <0.则( BC )
[解析] 对于命题 p :因为 x 2-2 x +1=( x -1)2≥0,所以 x 2+1≥2 x ,即不存在 x ,使 x 2+1<2 x ,故命题 p 是假命题,则命题 p 的否定是真命题.对于命题 q :若 mx 2- mx -1≠0恒成立,则当 m =0时,-1≠0,原不等式恒成立;当 m ≠0时,Δ= m 2+4 m <0,得-4< m <0.综合得-4< m ≤0,故命题 q 是假命题,则命题 q 的否定是真命题.综上所述,选项A错误、B正确、C正确、D错误.故选BC.
13. [多选/2024广东广州模拟]下列命题中为真命题的是( CD )
相关课件
这是一份第17讲 导数与函数的单调性(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版),共30页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,大于0,小于0等内容,欢迎下载使用。
这是一份第15讲 函数模型的应用(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版),共38页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,数学建模的过程,给出下列四个结论等内容,欢迎下载使用。
这是一份第13讲 函数的图象(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版),共31页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,yfx-k,2对称变换,3伸缩变换,作函数的图象的策略,角度1研究函数性质等内容,欢迎下载使用。










