

福建省福州第十九中学2023-2024学年八年级下学期期中复习数学试题(1)
展开
这是一份福建省福州第十九中学2023-2024学年八年级下学期期中复习数学试题(1),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题 (每小题4分,共40分)
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
第2题图
2.如图是用尺规平分一个已知角,能说明∠AOP=∠BOP的依据是( )
A.SSS B.SAS C.SSA D.AAS
3.下列计算正确的是( )
A. B.
C. D.
4.如图,点D、E分别是AC,AB的中点,DE=3,则池塘的宽度BC为( )
第4题图
A.3 B.4 C.5 D.6
5.下列各曲线中,不能表示y是x的函数的是( )
D
C
B
A
x
y
x
y
x
y
x
y
6.在以下列线段a、b、c的长为三角形的三边,不能构成直角三角形的是( )
A、a=11,b=12,c=15 B、a=b=5,c=
C、a:b:c=1: :2 D、a=9,b=41,c=40
7.下列从左往右的变形属于因式分解的是( )
A、 B、
第9题图
C、 D、
8.已知是一个完全平方式,则k的值是( )
A、 8 B、±8 C、16 D、 ±16
9.如图,△ABC中,∠ACB=90°,点D是AB边上动点,DE∥AC,
DF∥BC,若BC=3,AC=4,则EF的最小值为( )
A.5 B.3.5 C.2.5 D.2.4第10题图
如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交
对角线BD于点F,若∠DEF=∠DFE,则这个菱形的面积为( )
A.16 B. C. D.30
第12题图
二、填空题 (每小题4分,共24分)
11.函数中,自变量的取值范围是 .
12.如图,△ABC中,∠ACB=90°,D是AB中点,∠A=30°,若
BC=2,则CD的长为 .
13.已知a,b是两个连续整数,且a<﹣1<b,则ab=
14.已知菱形ABCD的对角线AC=6,BD=8,菱形的边长为 .
如图,平面直角坐标系中,A(0,2)点B是轴上的动点,△ABC是等边三角形,
连接OC,则OC的最小值是 .
第16题图
第15题图
16.如图,□ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC,BD于点E、P,连接OE,∠ADC=60°,AB=,则下列结论:
①∠CAD=30°;
②BD=;
③;
④。
其中结论正确的是 (只填写序号)。
三、解答题 (86分)
(8分)计算:(1) (2)
(8分)如图,已知E、F在□ABCD的对角线BD上,且AE∥CF.求证:BE=DF.
第18题图
19.(8分)先化简:,再从0≤≤4中选取一个适合的整数代入求值。
20.(8分)去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向,B地的西偏北45°方向。C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
第20题图
(参考数值:≈1.732)
第21题图
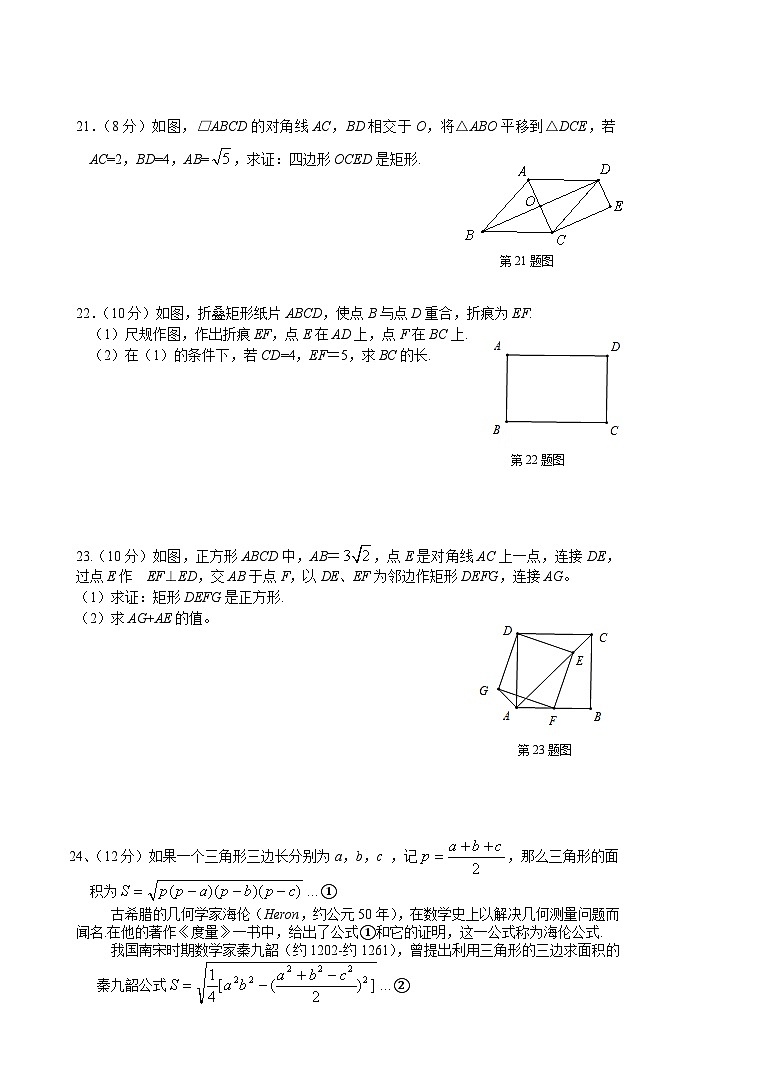
21.(8分)如图,□ABCD的对角线AC,BD相交于O,将△ABO平移到△DCE,若AC=2,BD=4,AB=,求证:四边形OCED是矩形.
22.(10分)如图,折叠矩形纸片ABCD,使点B与点D重合,折痕为EF.
第22题图
(1)尺规作图,作出折痕EF,点E在AD上,点F在BC上.
(2)在(1)的条件下,若CD=4,EF=5,求BC的长.
第23题图
23.(10分)如图,正方形ABCD中,AB=,点E是对角线AC上一点,连接DE,过点E作 EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG。
(1)求证:矩形DEFG是正方形.
(2)求AG+AE的值。
24、(12分)如果一个三角形三边长分别为a,b,c ,记,那么三角形的面
积为…①
古希腊的几何学家海伦(Hern,约公元50年),在数学史上以解决几何测量问题而
闻名.在他的著作《度量》一书中,给出了公式①和它的证明,这一公式称为海伦公式.
我国南宋时期数学家秦九韶(约1202-约1261),曾提出利用三角形的三边求面积的秦九韶公式…②
这两个公式实质上是同一个公式,所以也称①为海伦—秦九韶公式.
设a,b,c为△ABC的三边,当a=4,b=5,c=6时,求的面积.
请你对公式②进行变形,推导出公式①.
25、(14分)如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合),DE∥AB交AC于点F,CE∥AM,连接AE
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形.
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM,求∠CAM的度数.
2023-2024学年第二学期八年级数学期中复习试题(1)
班级 姓名 座号 评价
一、选择题 (每小题4分,共40分)
1.下列二次根式中,最简二次根式是( B )
A. B. C. D.
第2题图
2.如图是用尺规平分一个已知角,能说明∠AOP=∠BOP的依据是( A )
A.SSS B.SAS C.SSA D.AAS
3.下列计算正确的是( A )
A. B.
C. D.
4.如图,点D、E分别是AC,AB的中点,DE=3,则池塘的宽度BC为( D )
第4题图
A.3 B.4 C.5 D.6
5.下列各曲线中,不能表示y是x的函数的是( C )
D
C
B
A
x
y
x
y
x
y
x
y
6.在以下列线段a、b、c的长为三角形的三边,不能构成直角三角形的是( A )
A、a=11,b=12,c=15 B、a=b=5,c=
C、a:b:c=1: :2 D、a=9,b=41,c=40
7.下列从左往右的变形属于因式分解的是( C )
A、 B、
第9题图
C、 D、
8.已知是一个完全平方式,则k的值是( D )
A、 8 B、±8 C、16 D、 ±16
9.如图,△ABC中,∠ACB=90°,点D是AB边上动点,DE∥AC,
DF∥BC,若BC=3,AC=4,则EF的最小值为( D )
A.5 B.3.5 C.2.5 D.2.4第10题图
10.如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交
对角线BD于点F,若∠DEF=∠DFE,则这个菱形的面积为( B )
A.16 B. C. D.30
二、填空题 (每小题4分,共24分)
第12题图
11.函数中,自变量的取值范围是 .
12.如图,△ABC中,∠ACB=90°,D是AB中点,∠A=30°,若
BC=2,则CD的长为 2 .
13.已知a,b是两个连续整数,且a<﹣1<b,则ab= 8
14.已知菱形ABCD的对角线AC=6,BD=8,菱形的边长为 5 .
15.如图,平面直角坐标系中,A(0,2)点B是轴上的动点,△ABC是等边三角形,
连接OC,则OC的最小值是 1 .
第16题图
第15题图
16.如图,□ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC,BD于点E、P,连接OE,∠ADC=60°,AB=,则下列结论:
①∠CAD=30°;
②BD=;
③;
④。
其中结论正确的是 ①③④ (只填写序号)。
三、解答题 (86分)
17.(8分)计算:(1) (2)
解:原式= 解:原式=
第19题图
18.(8分)如图,已知E、F在□ABCD的对角线BD上,且AE∥CF.求证:BE=DF.
证明:∵ABCD是平行四边形 ∴AB=CD,AB∥CD
∴∠ABE=∠CDF
∵AE∥CF. ∴∠AED=∠CFB ∴∠AEB=∠CFD
∴△ABE≌△CDF ∴BE=DF
19.(8分)先化简:,再从0≤≤4中选取一个适合的整数代入求值。
解:原式=
要使分式有意义,,取,原式=.
20.(8分)去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向,B地的西偏北45°方向。C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
第20题图
(参考数值:≈1.732)
解:不会穿过公园.理由如下:过C作CD⊥AB于D.
D
依题意:∠CAD=30°,∠CBD=45°.设CD=km
则AC=km,BD=km
据勾股定理,
∵AB=2 ∴ ∴2.732=2 ∴>0.7
∴计划修筑的这条公路不会穿过公园.
第21题图
21.(8分)如图,□ABCD的对角线AC,BD相交于O,将△ABO平移到△DCE,若AC=2,BD=4,AB=,求证:四边形OCED是矩形.
证明:∵ABCD是平行四边形
∴OB=,OA
∵AB= ∴ ∴∠AOB=90°
由平移知:OC∥DE,OD∥CE ∴四边形OCED是平行四边形
∴□OCED是矩形.
第22题图
22.(10分)如图,折叠矩形纸片ABCD,使点B与点D重合,折痕为EF.
(1)尺规作图,作出折痕EF,点E在AD上,点F在BC上.
(2)在(1)的条件下,若CD=4,EF=5,求BC的长.
解:(1)如图所示,折痕EF即为所求.
(2)连接BE,DF,作FP⊥AD于P。
则四边形PFCD是矩形,四边形EBFD是菱形.
设PD=FC=,
∵∠EPF=90°,EF=5,PF=4
∴EP=3,即有.
∵∠C=90°,即
∴
∴,即BC=BF+FC=.
第23题图
23.(10分)如图,正方形ABCD中,AB=,点E是对角线AC上一点,连接DE,过点E作 EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG。
(1)求证:矩形DEFG是正方形.
(2)求AG+AE的值。
证明:(1)过E作EN⊥AD于N,
EM⊥AB于M.
∵AE是正方形ABCD的对角线
∴AC平分∠DAB
∴EN=EM
∵∠ENA=∠DAM=∠EMA=90° ∴ ∠NEM=90°
∴∠NEF+∠FEM=90°
∵EF⊥ED ∴∠NEF+∠NED=90° ∴ ∠FEM=∠NED
∵∠DNE=∠EMF=90° EN=EM ∴△DEN≌△FEM ∴EN=EF
∵DEFG是矩形 ∴矩形DEFG是正方形.
(2)∵DEFG是正方形 ∴DG=DE ∠GDE=∠ADC=90° ∴∠GDA=∠EDC
∵ABCD是正方形 ∴AD=DC ∴△DGA≌△DEC ∴AG=EC
∴AG+AE=EC+AC=AC ∵AB= ∠ABC=90° AB=BC ∴AC=6
∴AG+AE=6.
24、(12分)如果一个三角形三边长分别为a,b,c ,记,那么三角形的面
积为…①
古希腊的几何学家海伦(Hern,约公元50年),在数学史上以解决几何测量问题而
闻名.在他的著作《度量》一书中,给出了公式①和它的证明,这一公式称为海伦公式.
我国南宋时期数学家秦九韶(约1202-约1261),曾提出利用三角形的三边求面积的秦九韶公式…②
这两个公式实质上是同一个公式,所以也称①为海伦—秦九韶公式.
设a,b,c为△ABC的三边,当a=4,b=5,c=6时,求的面积.
请你对公式②进行变形,推导出公式①.
解:解:(1)当a=4,b=5,c=6时,.
∴,,
∴=.
(2)∵ ∴,,
∴=
=
=
=
=
==
25、(14分)如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合),DE∥AB交AC于点F,CE∥AM,连接AE
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形.
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM,求∠CAM的度数.
如图1:用SAS证明△ABM≌△EDC,可得AB=EM且有AB∥DE,四边形ABDE是平行四边形。
如图2:法一:过M作MN∥DE。 则DMNE为平行四边形DE=MN,易证△ABM≌△NMC得AB=MN=DE,且有AB∥DE,所以ABDE是平行四边形.
如图2:法二:延长BA到Q使AQ=AB,
连接QC,可证Q、E、C三点共线,则ADEQ为平行四边形,得BA=AQ=ED,且有AB∥DE,所以ABDE是平行四边形
如图3:法一:取HC中点I,连接MI,MI为△CBH中位线,。取AM中点K,中线KI=,△KIM为等边三角形,可求得∠MAC=30°.
如图3:法二:延长EA到G,使得AG=BH。连接GB,则可得AGBH为矩形,BH=AG=AM。连接MH、MG。中线MH=BM=MC,可证得△MBG≌△MHA,得GM=MA=AG
△AGM为等边三角形,可求得∠MAC=30°.
相关试卷
这是一份2024年福建省福州第十九中学中考模拟数学试题,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份福建省福州第十九中学2023-2024学年七年级下学期月考数学试题(含答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份25,福建省福州第十九中学2023-2024学年九年级下学期期中数学试题(无答案),共6页。试卷主要包含了04 命题人,实数的相反数是等内容,欢迎下载使用。









