陕西省西安市临潼区华清中学2024-2025学年高二上学期开学摸底测试数学试卷（原卷版+解析版）

这是一份陕西省西安市临潼区华清中学2024-2025学年高二上学期开学摸底测试数学试卷（原卷版+解析版），文件包含陕西省西安市临潼区华清中学2024-2025学年高二上学期开学摸底测试数学试卷原卷版docx、陕西省西安市临潼区华清中学2024-2025学年高二上学期开学摸底测试数学试卷解析版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。
注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效．
3．回答第Ⅱ卷时，将答案写在答题卡上．写在本试卷上无效．
4．考试结束后，将本试卷和答题卡一并交回．
第Ⅰ卷（选择题）
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
1. 已知复数（为虚数单位），则实数值为（ ）
A. B. 1C. 2D. 3
【答案】D
【解析】
【分析】由已知可得，根据复数乘法运算法则，和复数相等的充要条件，即可求解.
【详解】，
故选:D.
【点睛】本题考查复数的代数运算、复数相等的应用，属于基础题.
2. 设集合，，则（ ）
A. B. C. D.
【答案】C
【解析】
【分析】求解集合A,然后进行交集补集运算即可.
【详解】集合,
或,则
故选：C
3. 已知向量，且，则的值是（ ）
A. B. C. D. 6
【答案】D
【解析】
【分析】根据可得，进而利用向量的数量积的坐标表示可得结果．
【详解】因为，即，
化简，整理得，
则，解得.
故选：D
4. 已知，为两个不重合的平面，l，m为两条不同的直线，（ ）
A. 若，，则B. 若，，则
C. 若，，则D. 若，，则
【答案】D
【解析】
【分析】根据线面平行的判定定理和性质定理，结合线面垂直的性质定理逐一判断即可.
【详解】对于A，若，，则或，故A错误；
对于B，若，，则或，故B错误；
对于C，若，，则或，故C错误；
对于D，若，，由面面平行的性质定理可得，故D正确.
故选：D
5. 下列说法中正确的是（ ）
A. 若事件与事件是互斥事件，则
B. 对于事件和，
C. 一个人打靶时连续射击两次，则事件“至少有一次中靶”与事件“至多有一次中靶”是对立事件
D. 把红、橙、黄、绿4张纸牌随机分给甲、乙、丙、丁4人，每人分得1张，则事件“甲分得红牌”与事件“乙分得红牌”是互斥事件
【答案】D
【解析】
【分析】根据互斥事件、对立事件以及事件的关系与运算逐一判断即可.
【详解】选项A，因为事件与事件是互斥事件，但不一定对立，所以不一定成立，故选项A错误；
选项B，因为事件和不一定是互斥事件，所以没有，故选项B错误；
选项C，因为事件“至少有一次中靶”与事件“至多有一次中靶”，可以同时发生，故选项C错误；
选项D，因为件“甲分得红牌”与事件“乙分得红牌”不能同时发生，所以这两事件是互斥事件，故选项D正确.
故选：D.
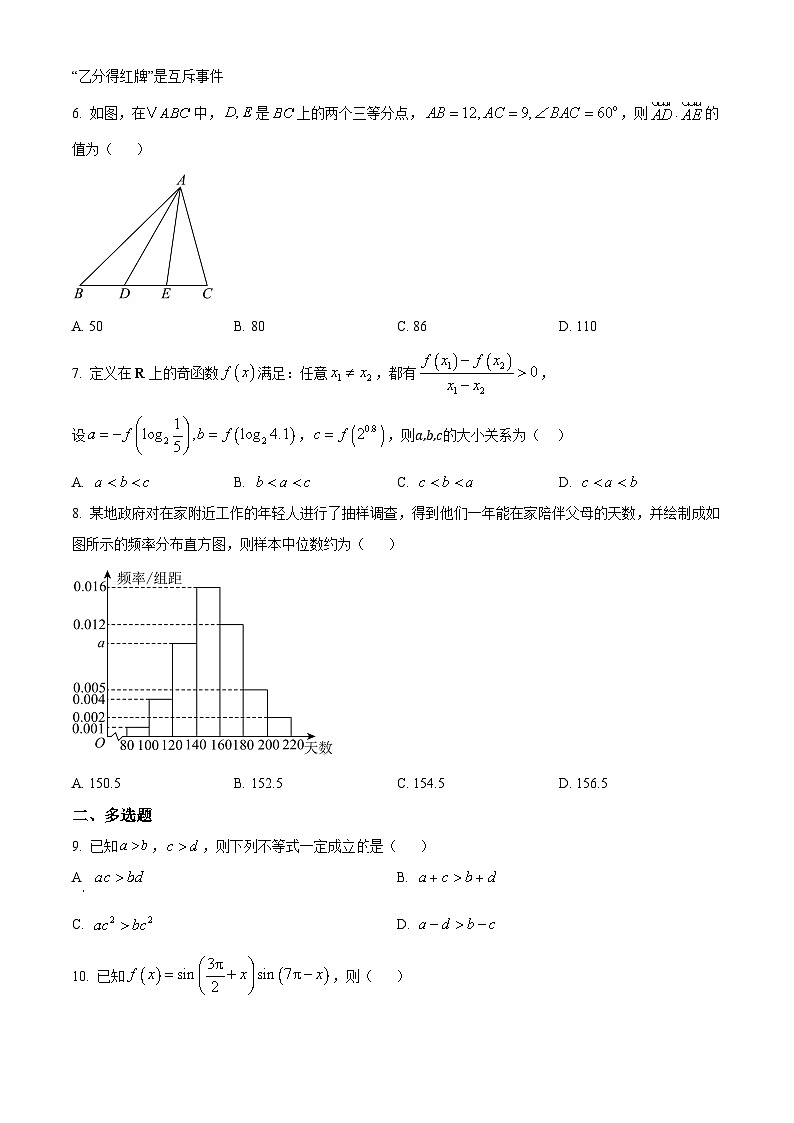
6. 如图，在中，是上的两个三等分点，，则的值为（ ）
A. 50B. 80C. 86D. 110
【答案】B
【解析】
【分析】根据题意利用平向量基本定理将用表示出来，然后利用数量积的运算律求解即可.
【详解】因为在中，是上的两个三等分点，，
所以，
，
所以
.
故选：B
7. 定义在R上的奇函数满足：任意，都有，
设，，则a,b,c的大小关系为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】由题意可得在R上单调递增，，利用对数函数及指数函数的单调性可得，从而即可得答案.
【详解】因为是在R上的奇函数，且任意，都有，
所以在R上单调递增，
又因为，
所以，
又因为，，
所以，
所以
即.
故选：C.
8. 某地政府对在家附近工作的年轻人进行了抽样调查，得到他们一年能在家陪伴父母的天数，并绘制成如图所示的频率分布直方图，则样本中位数约为（ ）
A. 150.5B. 152.5C. 154.5D. 156.5
【答案】B
【解析】
【分析】先根据频率之和为1求出未知数，再找到频率之和为0.5所在的区间即可根据频率分布直方图进行求解中位数.
【详解】依题意，，解得，
显然，，
所以样本中位数为.
故选：B
二、多选题
9. 已知，，则下列不等式一定成立的是（ ）
A. B.
C. D.
【答案】BD
【解析】
【分析】通过举反例判断选项AC错误；利用作差法判断B选项，利用不等式的性质判断D选项即可.
【详解】对于A，当时，，故选项A错误；
对于B，因为,所以，所以，故选项B正确；
对于C，当时，，故选项C错误；
对于D，因为，所以，又，所以，故选项D正确；
故选：BD.
10. 已知，则（ ）
A. 是奇函数
B. 的最小正周期是
C. 图象的一个对称中心是
D. 上单调递增
【答案】AC
【解析】
【分析】由三角恒等变换化简解析式，由定义判断A；由周期公式判断B；由性质判断CD.
详解】，
对于A：，即是奇函数，故A正确；
对于B：的最小正周期是，故B错误；
对于C：令，当时，图象的对称中心是，故C正确；
对于D：，函数在上单调递增，所以上单调递减，故D错误；
故选：AC
11. 如图，正方体的棱长为1，P是线段上的动点，则下列结论正确的是（ ）
A. 三棱锥的体积为定值
B. 平面
C. 的最小值为
D. 当，C，，P四点共面时，四面体的外接球的体积为
【答案】ABD
【解析】
【分析】A选项，求出为定值，且P到平面的距离为1，从而由等体积得到锥体体积为定值；B选项，证明出面面平行，得到线面平行；
C选项，将两平面展开到同一平面，连接，交于点，此时最小，最小值即为的长，由勾股定理得到最小值；
D选项，点P在点B处，，C，，P四点共面，四面体的外接球即正方体的外接球，求出正方体的外接球半径，得到外接球体积.
【详解】对于A，因为不在平面内，平面，
所以平面，又，
所以点到平面的距离为，
又为定值，
故定值，A正确；
对于B，因为，平面，平面，所以平面，
同理可知平面，
又，平面，
所以平面平面，
由于平面，故平面，B正确.
对于C，展开两线段所在的平面，得矩形及等腰直角三角形，
连接，交于点，此时最小，最小值即为的长，
过点作⊥，交的延长线于点，
其中，
故，又勾股定理得，C正确；
对于D，点P在点B处，，C，，P四点共面，
四面体的外接球即正方体的外接球，
故外接球的半径为，所以该球的体积为，D正确.
故选：ABD
【点睛】特殊几何体的内切球或外接球的问题，常常进行补形，转化为更容易求出外接球或内切球球心和半径的几何体，比如墙角模型，对棱相等的三棱锥常常转化为棱柱来进行求解.
三、填空题
12. 已知正数，满足，则的最小值为__________.
【答案】
【解析】
【分析】根据正数，满足，可得，
再由，利用基本不等式即可求解.
【详解】由正数，满足，可得，
所以，
当且仅当，，即时取等号，
所以的最小值为.
故答案为：.
13. 某几何体底面的直观图为如图矩形，其中，该几何体底面的面积为________．
【答案】
【解析】
【分析】根据直观图，得到底面平面图形的形状和图形的高，根据平行四边形的面积公式求出底面积.
【详解】在直观图中，令轴与交于点，则，
直观图还原为平面图形如图，
根据直观图与原图的关系可得：，
故该几何体的底面是平行四边形，其面积为.
故答案为：.
14. 已知中，角A，B，C所对的边分别为a，b，c.若，，则___________.
【答案】##0.75
【解析】
【分析】利用正弦定理、三角变换公式可得及，故可得，消元后可得的值.
【详解】由正弦定理可得，
故，
故，
整理得到，
而，故，所以，
故，解得或，
若，则，故同为钝角，这与矛盾，
故.
故答案为：.
四、解答题
15. 已知函数满足．
（1）求的解析式；
（2）求函数在上的值域．
【答案】（1）
（2）．
【解析】
【分析】（1）利用换元法进行求解即可；
（2）根据二次函数的单调性进行求解即可.
【小问1详解】
令，得，
则，
故的解析式为．
【小问2详解】
由题意得，
函数的对称轴为，
所以在上单调递减，在上单调递增，
所以，
，
故在上的值域为．
16. 正四棱台两底面边长分别为2和4．
（1）若侧棱长为，求棱台的表面积；
（2）若棱台的侧面积等于两底面面积之和，求它的高．
【答案】（1）
（2）
【解析】
【分析】（1）设分别为上，下底面的中心，分别取的中点，利用梯形求出斜高，从而求出表面积；
（2）根据已知条件求出斜高, 再由直角梯形求出四棱台的高.
【小问1详解】
如图，设分别为上，下底面的中心，
分别取的中点，连接，则为正四棱台的斜高，
，
则棱台的表面积.
【小问2详解】
两底面面积之和为，
正四棱台的侧面积为，解得，
正四棱台的高.
17. 的内角A，B，C的对边分别为a，b，c，已知.
（1）求A；
（2）若，求面积的最大值.
【答案】（1）
（2）
【解析】
【分析】（1）由二倍角余弦公式及正弦边角关系得，根据余弦定理求的余弦值，进而确定其大小；
（2）由已知和余弦定理得，再由求面积最大值，注意取值条件.
【小问1详解】
由已知，
即，由正弦边角关系得，
所以，又，所以.
【小问2详解】
由余弦定理，得，又，
所以，当且仅当时等号成立，
所以，故的面积的最大值为.
18. 如图，在四棱锥中，底面ABCD，E是PC的中点，点F在棱BP上，且，四边形ABCD为正方形，.

（1）证明：；
（2）求三棱锥的体积；
（3）求二面角的余弦值.
【答案】（1）证明见解析
（2）
（3）
【解析】
【分析】（1）由线面垂直的判定求证；
（2）由转化求解；
（3）由线面垂直的性质得即二面角的平面角，即可求解．
【小问1详解】
证明：因为底面，底面，所以.
因为四边形为正方形，所以.
因为，所以平面.
因为平面，所以.
在中，，E是PC的中点，则.
因为，所以平面.
因为平面，所以.
因为，，所以平面.
因为平面，所以.
【小问2详解】
连接交于点，如图所示：

则，又底面，平面，得，
而，则平面，则点C到平面的距离为，
因为E是PC的中点，所以
，，，，
所以，，
所以.
【小问3详解】
解：由（1）可得平面，因为平面，平面，所以，.
为二面角的平面角.
，.
因为，所以，解得.
因为，即，所以.
故二面角的余弦值为.
19. 当我们沉浸在游戏世界中时，很容易忽视时间的流逝，甚至忘记自己的学业和生活.一些大学生因为过度沉迷网络游戏，导致学业成绩下滑，身体健康状态也受到影响.长时间盯着电脑屏幕，不仅会导致视力下降，还可能引发颈椎病等健康问题.更为严重的是，过度依赖虚拟世界的社交可能会削弱我们在现实生活中的社交能力，造成人与人之间的疏离感.某大学心理机构为了向大学生宣传沉迷网络游戏的危害，该机构随机选择了200位沉迷网络的大学生进行宣传，将这些大学生每天玩网络游戏的时间分成五段：，，，，（单位：小时），得到如图所示的频率分布直方图.
（1）求频率分布直方图中a的值；
（2）请估计这200位大学生每天玩网络游戏的平均时间（同组数据用区间的中点值代替）；
（3）现在从和两组中用分层抽样的方法抽取5人，再从这5人中随机抽取2人进行交流，求这2人每天玩网络游戏的时间所在区间不同的概率.
【答案】（1）0.1；
（2）7.4小时； （3）.
【解析】
【分析】（1）利用频率分布直方图tk 小矩形面积和为1求出值.
（2）利用频率分布直方图估计平均数的算法，列式计算即得.
（3）利用分层抽样求出指定两个区间的人数，再利用列举法求出古典概率.
【小问1详解】
由频率分布直方图，得，所以.
小问2详解】
每天玩网络游戏平均时间（小时）.
【小问3详解】
每天玩网络游戏的时间在和内的人数比为，
则用分层抽样的方法抽取的5人中，在内的有1人，记为，在内的有4人，记为，
这5人中随机抽取2人的试验的样本空间，共10个样本点，
玩网络游戏的时间所在区间不同的事件，共4个样本点，
所以这2人每天玩网络游戏的时间所在区间不同的概率.