初中数学北师大版（2024）九年级上册4 用因式分解法求解一元二次方程教学课件ppt

这是一份初中数学北师大版（2024）九年级上册4 用因式分解法求解一元二次方程教学课件ppt，共21页。PPT课件主要包含了本节课涉及，小颖的解法，小明的解法，小亮的解法，分析1，提公因式x，等价于，x0或5x–40，x10x2，解一元一次方程等内容，欢迎下载使用。
用因式分解法求解一元二次方程
1.理解用因式分解法解一元二次方程的依据.2.能用因式分解法(提公因式法、公式法)解某些数字系数的一元二次方程.3.能根据具体的一元二次方程的特征，灵活选择方程的解法.4.体验解决问题的方法多样性，提升学习数学的兴趣，并建立学好数学的自信心.
想一想：什么是因式分解？
把一个多项式分解成几个整式乘积的形式叫做因式分解.
你知道因式分解有哪些方法吗？
①提公因式法：ma + mb + mc = m(a+b+c)②公式法：平方差公式 a2–b2=(a+b)(a–b)完全平方公式 a±2ab+b =(a±b)2③十字相乘法:x2 +(a+b)x + ab =(x + a)(x +b)
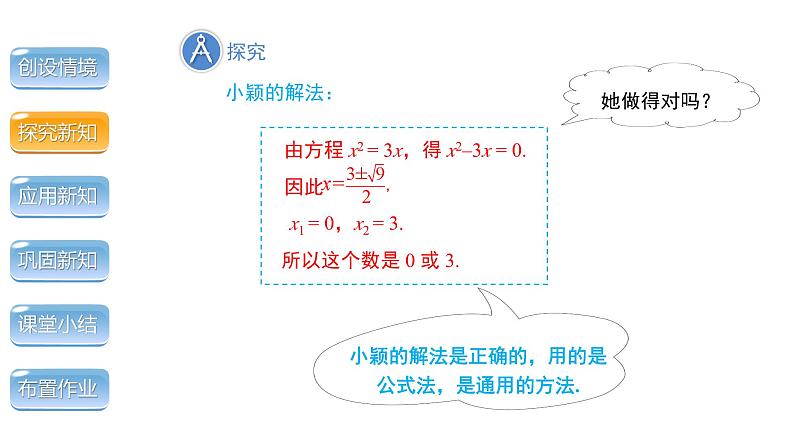
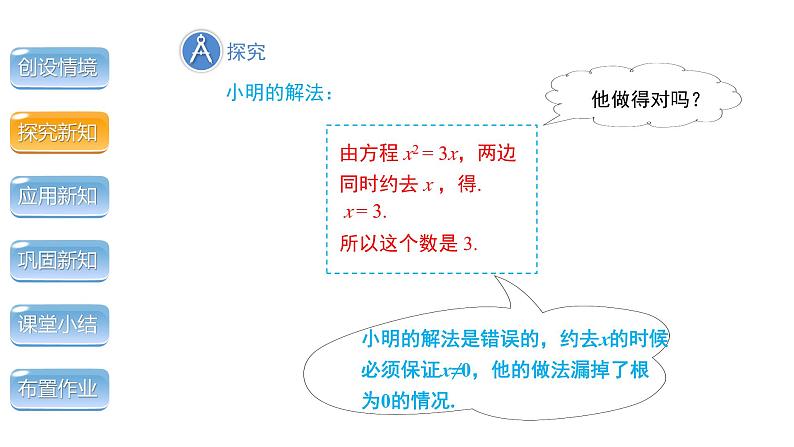
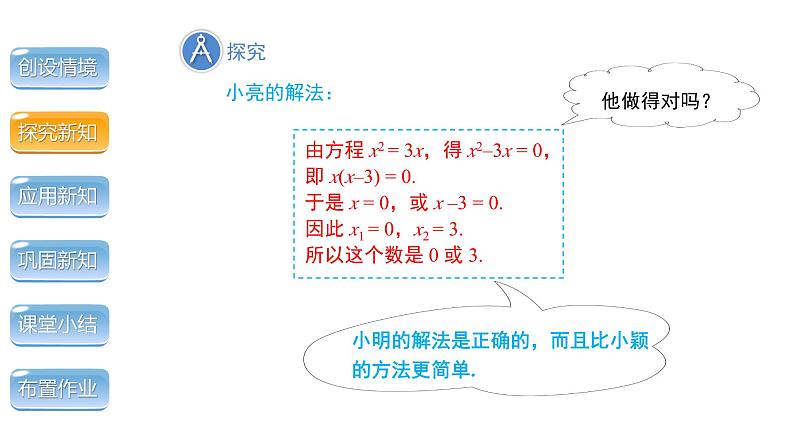
小颖、小明、小亮都设这个数为 x，根据题意，可得方程 : x2 = 3x.
问题 一个数的平方与这个数的 3 倍有可能相等吗？如果能，这个数是几？你是怎样求出来的？
小颖、小明、小亮都解了此方程，他们的解法各不相同，你觉得谁做的对呢？
你知道如何解此方程吗？
小颖的解法是正确的，用的是公式法，是通用的方法.
小明的解法是错误的，约去x的时候必须保证x≠0，他的做法漏掉了根为0的情况.
小明的解法是正确的，而且比小颖的方法更简单.
如果 ab = 0，那么 a = 0 或 b = 0 .
“或”是“二者中至少有一个成立”的意思，包括两种情况：二者同时成立、二者有一个成立. “且”是“二者同时成立”的意思.
说一说，你是怎么理解这句话的？
当一元二次方程的一边是 0，而另一边易于分解成两个一次因式的乘积时，我们就可以用因式分解的方法求解.
这种用因式分解解一元二次方程的方法称为因式分解法.
例 解下列方程： (1) 5x2 = 4x； (2) x(x–2)=x–2.
5x2=4x
5x2–4x=0
x(5x–4)=0
x(x–2)–(x–2)=0
(x–2)(x–1)=0
x–1=0或x–2=0
解：(1)原方程可变形为
5x2 – 4x = 0 ，
x(5x – 4) = 0 ，
x = 0 ，或 5x–4 = 0.
x(x–2) – (x–2) = 0 ，
(x–2)(x–1) = 0.
x–2 = 0 ，或 x–1= 0.
x1 = 2 ，x2 = 1.
用因式分解法解一元二次方程的步骤：
①方程右边化为______；②将方程左边分解成两个__________的乘积；③至少________因式为零，得到两个一元一次方程；④两个__________________就是原方程的解.
你能用因式分解法解方程 x2–4=0，(x+1)2–25 = 0 吗？
(x + 2)(x – 2) = 0.
x + 2 = 0 或 x –2 = 0.
x1 = –2，x2 = 2.
(x+1)2–25 = 0
(x +1+5)(x+1–5) = 0.
(x+6)(x–4) = 0.
x+6 = 0 或 x–4 = 0.
x1 = –6，x2 = 4.
1.用因式分解法解下列方程：(1) (x + 2)(x – 4) = 0； (2) 4x(2x + 1) = 3(2x + 1).
解：(1)(x + 2)(x – 4) = 0
x+2=0 或x–4=0.
x1 = –2，x2 = 4.
(2) 原方程可变形为
4x(2x + 1) – 3(2x + 1) = 0.
(2x + 1)(4x –3) = 0.
2x + 1 = 0 或 4x–3 = 0.
2.一个数平方的 2 倍等于这个数 的 7 倍，求这个数.
2x2 – 7x = 0.
x(2x – 7) = 0.
x = 0 或 2x –7 = 0.
用因式分解法解下列方程： (1)(4x –1)(5x + 7) = 0； (2) x(x + 2) = 3x + 6；
解：(1)(4x –1)(5x + 7) = 0
4x –1= 0 或 5x + 7= 0.
x(x + 2) = 3(x + 2).
x(x + 2) –3(x + 2) = 0.
(x + 2)(x –3) = 0.
x1 = –2，x2 =3.
用因式分解法解下列方程： (3) (2x + 3)2 = 4(2x + 3)； (4) 2(x –3)2 = x2 –9.
(2x+3)2 – 4(2x + 3)= 0.
(2x+3)(2x+3– 4)= 0.
2x + 3 = 0 或 2x–1 = 0.
2(x – 3)2 = (x + 3)(x –3).
2(x – 3)2 – (x + 3)(x – 3) = 0.
(x – 3) [2(x – 3)–(x + 3)] = 0.
(x –3) (x – 9) = 0.
x1 = 3，x2 = 9.
当一元二次方程的一边是 0，而另一边易于分解成两个一次因式的乘积时，我们就可以用因式分解的方法求解，这种解一元二次方程的方法称为因式分解法.
①方程右边化为0；②将方程左边分解成两个一次因式的乘积；③至少有一个因式为零，得到两个一元一次方程；④两个一元一次方程的解就是原方程的解.
教科书第48页习题2.7第2、3题