2024-2025学年广西南宁十四中九年级（上）开学数学试卷（含答案）

这是一份2024-2025学年广西南宁十四中九年级（上）开学数学试卷（含答案），共11页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列各式中是最简二次根式的是( )
A. 5B. 1C. 18D. 19
2.如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是( )
A. 2，3，4B. 3，4，5C. 6，8，10D. 5，12，13
3.从甲、乙、丙、丁中选一人参加诗词大会比赛，经过三轮初赛，他们的平均成续都是90分，方差分别是S甲2=3，S乙2=2.6，S丙2=2，S丁2=3.6，派谁去参赛更合适( )
A. 甲B. 乙C. 丙D. 丁
4.依据所标数据，下列图形中一定为平行四边形的是( )
A. B. C. D.
5.一次函数y=−5x+4的图象不经过( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
6.如图，在矩形ABCD中，对角线AC、BD相交于点O，AE⊥BD交BD于点E，∠AOB=110°，则∠DAE的度数为( )
A. 40° B. 35°
C. 30° D. 25°
7.“指尖上的非遗一一麻柳刺绣”，针线勾勒之间，绣出世间百态.在一幅长80cm，宽50cm的刺绣风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同)，则列出的方程为( )
A. (50+x)(80+x)=5400
B. (50−x)(80−x)=5400
C. (50+2x)(80+2x)=5400
D. (50−2x)(80−2x)=5400
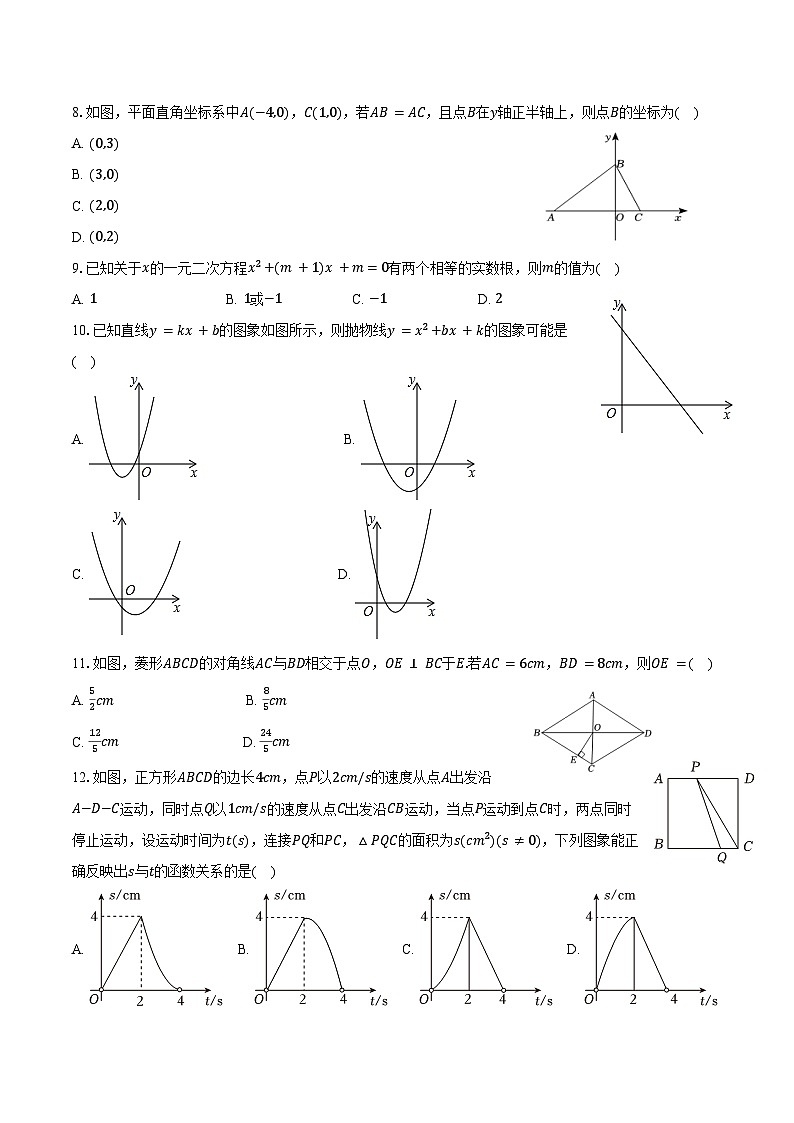
8.如图，平面直角坐标系中A(−4,0)，C(1,0)，若AB=AC，且点B在y轴正半轴上，则点B的坐标为( )
A. (0,3)
B. (3,0)
C. (2,0)
D. (0,2)
9.已知关于x的一元二次方程x2+(m+1)x+m=0有两个相等的实数根，则m的值为( )
A. 1B. 1或−1C. −1D. 2
10.已知直线y=kx+b的图象如图所示，则抛物线y=x2+bx+k的图象可能是( )
A. B.
C. D.
11.如图，菱形ABCD的对角线AC与BD相交于点O，OE⊥BC于E.若AC=6cm，BD=8cm，则OE=( )
A. 52cm B. 85cm
C. 125cm D. 245cm
12.如图，正方形ABCD的边长4cm，点P以2cm/s的速度从点A出发沿A−D−C运动，同时点Q以1cm/s的速度从点C出发沿CB运动，当点P运动到点C时，两点同时停止运动，设运动时间为t(s)，连接PQ和PC，△PQC的面积为s(cm2)(s≠0)，下列图象能正确反映出s与t的函数关系的是( )
A. B. C. D.
二、填空题：本题共6小题，每小题2分，共12分。
13.如果代数式 x+1有意义，那么x的取值范围是______．
14.某公司对A应聘者进行创新、综合知识、语言三项测试，其三项成绩分别为72分、50分、88分，若给这三个分数分别赋予权1，2，1，则A应聘者的加权平均分数为______分.
15.已知m，n是方程x2+4x−3=0的两个实数根，则m2+5m+n+2024的值是______．
16.如图，函数y=kx+b(k≠0)的图象经过点B(m,0)(m>1)，与函数y=2x的图象交于点A，则不等式kx+b≤2x的解集为______．
17.如图，用一面足够长的墙为一边，其余三边用总长34米的围栏建两个面积相同的生态园，两个生态园各留一扇宽为1米的门.由于场地限制，垂直于墙的一边长不超过6米(围栏宽忽略不计).每个生态园的面积为48平方米，则每个生态园垂直于墙的一边长为______．
18.在平面直角坐标系中，抛物线y=x2的图象如图所示，已知A点坐标为(1,1)，过点A作AA1//x轴交抛物线于点A1，过点A1作A1A2//OA交抛物线于点A2，过点A2作A2A3//x轴交抛物线于点A3，过点A3作A3A4//OA交抛物线于点A4……，依次进行下去，则点A2024的坐标为______．
三、计算题：本大题共1小题，共6分。
19.解方程：x2−4x−12=0．
四、解答题：本题共7小题，共66分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题6分)
计算： 8+ 27÷ 3− 3× 6．
21.(本小题10分)
已知二次函数y=x2−2x−3，请解答下列问题：
(1)在平面直角坐标系xOy中，画出这个二次函数的图象(不用列表)；
(2)此函数图象与x轴的交点坐标为______；
(3)直接写出当y>0时，x的取值范围．
22.(本小题10分)
学校组织八、九年级学生参加了“国家安全知识”测试(满分100分).已知八、九年级各有800人.现从两个年级分别随机抽取10名学生的测试成绩x(单位：分)进行统计：
八年级：86、94，79，84、71，90，76，83，90，87
九年级：88，76，90，78，87，93，75，87，87，79
整理如表：
根据以上信息，回答下列问题：
(1)填空：a= ______，b= ______；A同学说：“这次测试我得了86分，位于年级中等偏上水平”，由此可判断他是______年级的学生；
(2)学校规定测试成绩不低于85分为“优秀”，估计该校这两个年级测试成绩达到“优秀”的学生总人数；
(3)你认为哪个年级的学生掌握“国家安全知识”的总体水平较好？请从两个方面说明理由．
23.(本小题10分)
如图，在平行四边形ABCD中，对角线AC与BD相交于点O，过点O任作一条直线分别交AB，CD于点E，F．
(1)求证：△AOE≌△COF；
(2)若AB=8，BC=6，OE=3，求四边形BCFE的周长．
24.(本小题10分)
某商场以每件20元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于36元，经市场调查发现：该商品每天的销售量y(件)与每件售价x(元)之间符合一次函数关系，如图所示．
(1)求y与x之间的函数关系式；
(2)该商场销售这种商品要想每天获得600元的利润，每件商品的售价应定为多少元？
(3)设商场销售这种商品每天获利w(元)，当每件商品的售价定为多少元时，每天销售利润最大？最大利润是多少？
25.(本小题10分)
综合与实践

(1)【知识感知】如图1，我们把对角线互相垂直的四边形叫做垂美四边形，在我们学过的：①平行四边形②矩形③菱形④正方形中，能称为垂美四边形是______(只填序号)；
(2)【概念理解】如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由；
(3)【性质探究】如图1，垂美四边形ABCD的两对角线交于点O，试探究AB，CD，BC，AD之间有怎样的数量关系？写出你的猜想______；
(4)【性质应用】如图3，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE已知AC=4，AB=5，则GE长为______．
26.(本小题10分)
如图，在平面直角坐标系中，已知抛物线y1=−x2−6x．
(1)求抛物线y1的顶点P坐标；
(2)平移抛物线y1得抛物线y2，两抛物线交于点A，过点A作x轴的平行线分别交抛物线y1和平移后的抛物线y2于点B和点C(点B在点C的左侧)，抛物线y2的顶点为Q．
①平移后的抛物线y2的顶点在直线x=1上，点A的横坐标为−1，求抛物线y2的表达式；
②平移后的抛物线y2的顶点在直线x=1上，点A的横坐标为m(−3③设点A的横坐标为n，BC=10，设PQ2=y，求y关于n的函数表达式，并求y的最小值．
参考答案
1.A
2.A
3.C
4.C
5.C
6.B
7.C
8.A
9.A
10.B
11.C
12.B
13.x≥−1
14.65
15.2023
16.x≥1
17.4米
18.(1013,10132)
19.解：(x−6)(x+2)=0，
x−6=0或x+2=0，
所以x1=6，x2=−2．
20.解： 8+ 27÷ 3− 3× 6
=2 2+ 9−3 2
=3− 2．
21.(3,0)、(−1,0)
【解析】解：(1)y=x2−2x−3=(x−1)2−4，
函数的大致图象如下：
(2)(3,0)、(−1,0)；
(3)观察函数图象知，当y>0时，x的取值范围为：x>3或x<−1．
22(1)85，87，八；
(2)510×800+610×800=880(人)，
答：该校这两个年级测试成绩达到“优秀”的学生总人数大约为220人；
(3)我认为九年级的学生掌握国家安全知识的总体水平较好，
理由：因为八、九年级测试成绩的平均数相等，九年级测试成绩的方差小于八年级测试成绩的方差，所以九年级的学生掌握国家安全知识的总体水平较好．
23.(1)证明：∵四边形ABCD是平行四边形，
∴OA=OC，AB//CD，
∴∠FCO=∠EAO，∠CFO=∠AEO，
在△AOE和△COF中，
∠FCO=∠EAO∠CFO=∠AEOOA=OC，
∴△AOE≌△COF(AAS)；
(2)解：∵△AOE≌△COF，
∴OE=OF，AE=CF，
∴四边形BCFE的周长=BE+CF+BC+EF=BE+AE+BC+2OE=AB+BC+2OE=8+6+2×3=20．
24.解：(1)设y与x之间的函数关系式为y=kx+b(k≠0)，
由所给函数图象可知：25k+b=7035k+b=50，
解得：k=−2b=120，
∴y与x之间的函数关系式为y=−2x+120；
(2)根据题意得：(x−20)(−2x+120)=600，
整理，得：x2−80x+1500=0，
解得：x=30或x=50(舍去)，
答：每件商品的销售价应定为30元；
(3)∵y=−2x+120，
∴w=(x−20)y=(x−20)(−2x+120)=−2(x−40)2+800，
∴抛物线的对称轴为x=40，且开口向下，
∴当x<40时，y随x的增大而增大，
∵x≤36，
∴当x=36时，w有最大值，最大值为w最大=−2(36−40)2+800=768，
∴售价定38元/件时，每天最大利润为768元．
25.③④ AD2+BC2=AB2+CD2 73
【解析】解：(1)∵菱形和正方形的对角线均互相垂直，
∴菱形和正方形是垂美四边形，
故答案为：③④
(2)四边形ABCD是垂美四边形，理由如下：
连接AC，BD，如图所示：
∵AB=AD，CB=CD
∴点A在线段BD的垂直平分线上，点C在线段BD的垂直平分线上，
∴直线AC是线段BD的垂直平分线，
∴AC⊥BD
即：四边形ABCD是垂美四边形；
(3)∵AD2=AO2+DO2，BC2=BO2+CO2，AB2=AO2+BO2，CD2=CO2+DO2，
∴AD2+BC2=AO2+BO2+CO2+DO2=AB2+CD2，
故答案为：AD2+BC2=AB2+CD2；
(4)如图3，连接BE、CG，设AB与CE交于点M，
由题意得：AB=AE，AG=AC，∠BAE=∠GAC=90°，
∴∠BAE+∠CAB=∠GAC+∠CAB，
即：∠CAE=∠GAB，
∴△CAE≌△GAB(SAS)，
∴∠ABG=∠AEC，
∵∠AEC+∠AME=90°，∠AME=∠CMB，
∴∠ABG+∠CMB=90°，
∴CE⊥BG，
由(3)可得：GE2+BC2=CG2+BE2，
∵AC=AG=4，AB=AE=5，
∴BC= AB2−AC2=3,CG= AC2+AG2=4 2,BE= AB2+BE2=5 2，
∴GE2+9=32+50，
∴GE= 73．
26.解：(1)∵函数解析式为：y1=−x2−6x=−(x+3)2+9，
∴点P的坐标为：(−3,9)，
(2)①当x=−1时，y1=−x2−6x=5，
即A(−1,5)，
设y2=−(x−1)2+t，
将点A的坐标代入上式得：5=−(−1−1)2+t，
解得：t=9，
即y2=−(x−1)2+9；
②由题意得：xQ−xP=1−(−3)=4，
∴根据抛物线的对称性知：BC=2(xQ−xP)=8；
③由②知，xQ−xP=12BC，
∵BC=10，
∴xQ−xP=12BC=5，
∴xQ=−3+5=2，
设点Q(2,t)，抛物线的表达式为：y2=−(x−2)2+t，
∴当x=n时，y1=−x2−6x=−n2−6n，
∴点A(n,−n2−6n)，
将点A的坐标代入上式得：−n2−6n=−(n−2)2+t，
解得：t=4−10n，
即点Q(2,4−10n)，
∵点P的坐标为：(−3,9)，
∴y=PQ2=(2+3)2+(4−10n−9)2=100n2+100n+50=100(n+12)2+25，
∴配方可得：y=100(n+12)2+25，
∵100>0，
∴y有最小值，
∴当n=−12时，y的最小值为25． 年级
平均数
中位数
众数
方差
八年级
84
a
90
44.4
九年级
84
87
b
36.6