2022-2023学年安徽省淮北四中八年级（上）期末数学试卷(含答案，沪科版)

这是一份2022-2023学年安徽省淮北四中八年级（上）期末数学试卷(含答案，沪科版)，共11页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1．（4分）平面直角坐标系中，点P（﹣3，﹣4）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．（4分）函数的自变量x的取值范围是（ ）
A．x≠3B．x＞3C．x＜3D．x＝3
3．（4分）下面四幅图分别是由体育运动长鼓舞、武术、举重、摔跤抽象出来的简笔画，其中是轴对称图形的是（ ）
A．B．C．D．
4．（4分）一个三角形三个内角的度数之比为2：5：7，这个三角形一定是（ ）
A．等腰三角形B．直角三角形C．锐角三角形D．钝角三角形
5．（4分）已知一次函数y＝（k﹣1）x+b（k和b是常数）的图象经过原点，则（ ）
A．k≠﹣1，b≠0B．k≠1，b＝0C．k＝0，b≠0D．k＝0，b＝0
6．（4分）如图，在△ABC中，AB＝AC，延长BC到点E，延长CB到点D，使得BD＝CE，判定△ACD≌△ABE的理由是（ ）
A．SSSB．SASC．ASAD．AAS
7．（4分）已知三角形的三边长分别是4，8，a+1，则a的取值可能是（ ）
A．10B．11C．12D．13
8．（4分）如图，△ABC≌△AED，点E在线段BC上，∠1＝60°，则∠AEC等于（ ）
A．100°B．110°C．120°D．125°
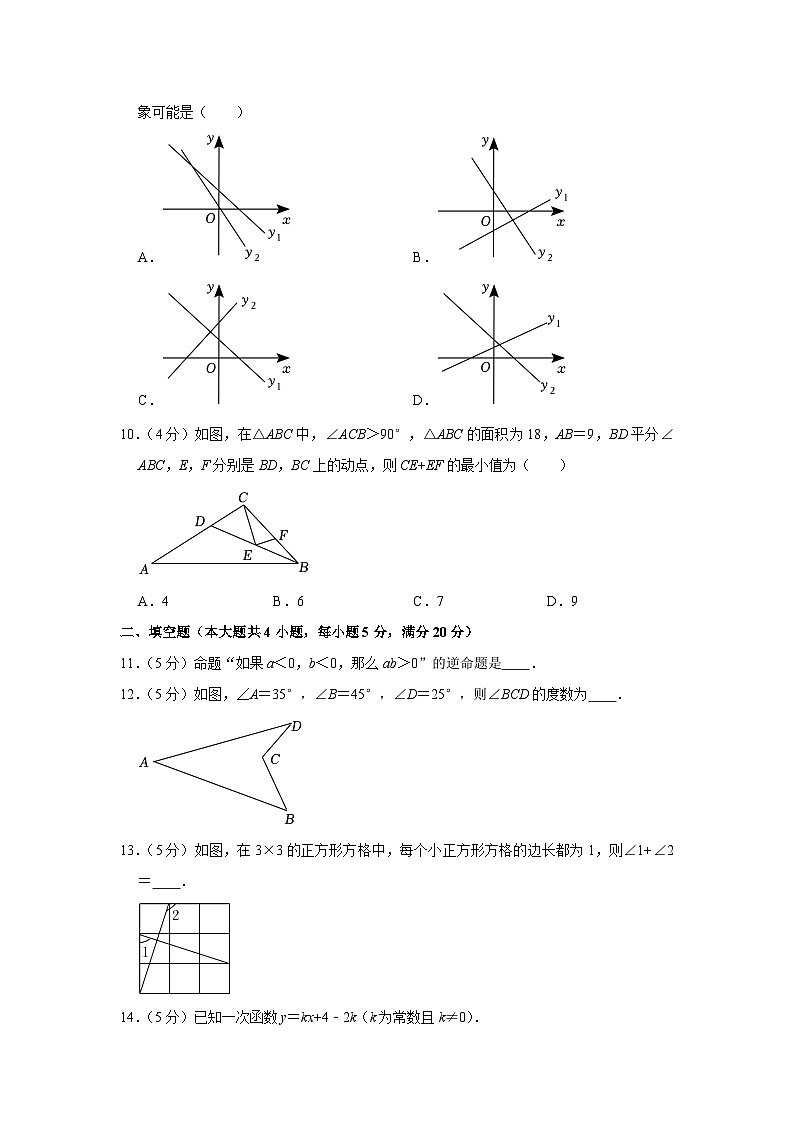
9．（4分）一次函数y1＝mx+n（m，n是常数）与y2＝nx+m在同一平面直角坐标系中的图象可能是（ ）
A．B．
C．D．
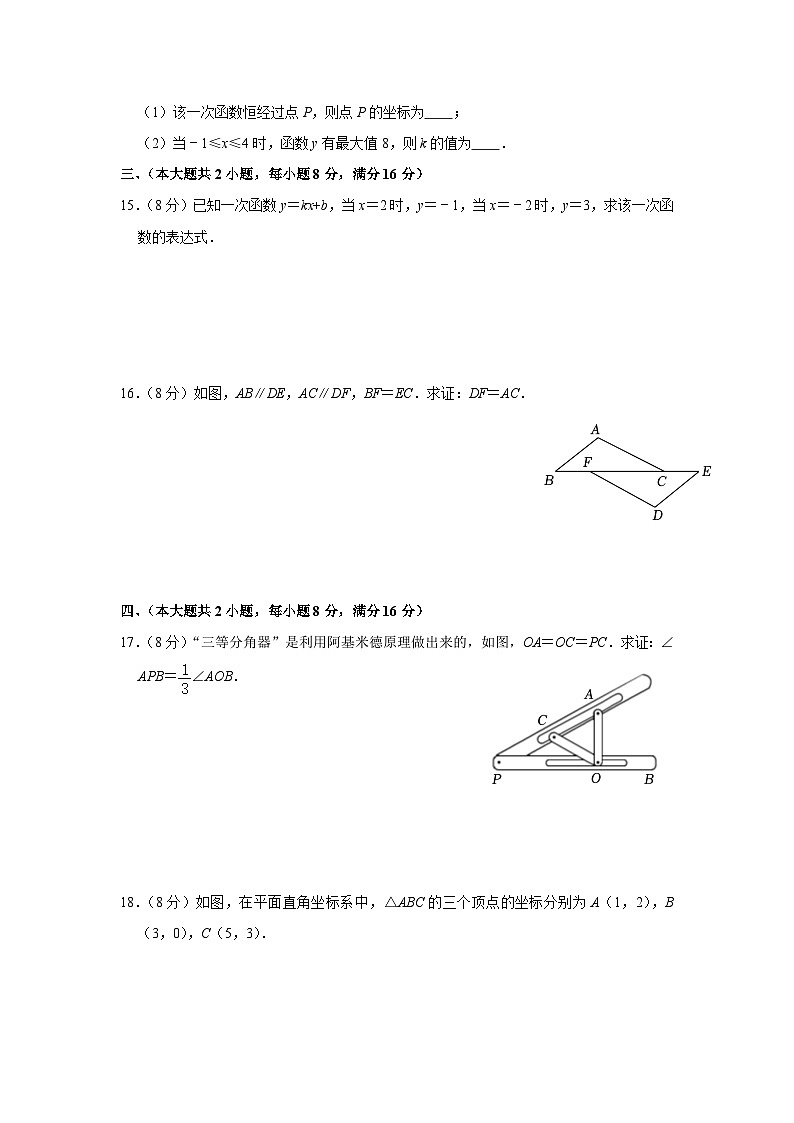
10．（4分）如图，在△ABC中，∠ACB＞90°，△ABC的面积为18，AB＝9，BD平分∠ABC，E，F分别是BD，BC上的动点，则CE+EF的最小值为（ ）
A．4B．6C．7D．9
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）命题“如果a＜0，b＜0，那么ab＞0”的逆命题是 ．
12．（5分）如图，∠A＝35°，∠B＝45°，∠D＝25°，则∠BCD的度数为 ．
13．（5分）如图，在3×3的正方形方格中，每个小正方形方格的边长都为1，则∠1+∠2＝ ．
14．（5分）已知一次函数y＝kx+4﹣2k（k为常数且k≠0）．
（1）该一次函数恒经过点P，则点P的坐标为 ；
（2）当﹣1≤x≤4时，函数y有最大值8，则k的值为 ．
三、（本大题共2小题，每小题8分，满分16分）
15．（8分）已知一次函数y＝kx+b，当x＝2时，y＝﹣1，当x＝﹣2时，y＝3，求该一次函数的表达式．
16．（8分）如图，AB∥DE，AC∥DF，BF＝EC．求证：DF＝AC．
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）“三等分角器”是利用阿基米德原理做出来的，如图，OA＝OC＝PC．求证：∠APB＝∠AOB．
18．（8分）如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（1，2），B（3，0），C（5，3）．
（1）请画出△ABC关于y轴对称的△A1B1C1（点A1，B1，C1的对称点分别为点A，B，C），并写出点A1，B1，C1的坐标．
（2）求△ABC的面积．
五、（本大题共2小题，每小题10分，满分20分）
19．（10分）在平面直角坐标系中，某点按向下、向右、向上、向右的方向依次不断移动，每次移动1个单位长度，其运动路线如图所示，根据图形规律，解决下列问题．
（1）点A5的坐标为 ，点A9的坐标为 ，点A13的坐标为 ，点A4n+1的坐标为 ．
（2）直接写出点A1到点A2025的距离： ．
20．（10分）如图，在平面直角坐标系中，直线l1：y＝ax+4与x轴，y轴分别交于点B，A，且与直线l2：y＝kx相交于点C（2，2）．
（1）求a和k的值．
（2）直线l1，l2与x轴围成的三角形面积为 ．
（3）kx≥ax+4≥0的解集为 ．
六、（本题满分12分）
21．（12分）如图，△ADE和△ABC都是等边三角形，M，N分别是CE，BD的中点，连接AM，AN，MN．
求证：（1）△ABD≌△ACE；
（2）△AMN是等边三角形．
七、（本题满分12分）
22．（12分）某学校购买一批篮球和排球，已知购买2个篮球和1个排球需170元，购买5个篮球和2个排球需400元．
（1）分别求篮球和排球的单价．
（2）该学校准备购买篮球和排球共100个，每种球至少买一个且篮球个数不少于排球个数的3倍．
①设购买篮球m（个），总费用为W（元），写出W关于m的函数表达式并写出自变量的取值范围；
②请设计总费用最低的购买方案，并求出最低费用．
八、（本题满分14分）
23．（14分）在Rt△ABC中，∠ACB＝90°，AC＝BC，CE是∠ACB内的射线，分别过点A，B作AD⊥CE，BE⊥CE，垂足分别为D，E．
（1）证明：△ACD≌△CBE．
（2）若AD＝6，BE＝2，求DE的长．
（3）如图2，O是AB的中点，连接OD，OE．先判断△DOE的形状，再给出证明．
参考答案与试题解析
一、选择题（本大题共10小题，每小题4分，满分40分）
1-5CACBB 6-10BACBA
二、填空题（本大题共4小题，每小题5分，满分20分）
11．假12．105°13．180°14．（1）（2，4）（2）﹣或2
三、（本大题共2小题，每小题8分，满分16分）
15．解：根据题意得，
解得，
所以一次函数的表达式为y＝﹣x+1．
16．证明：∵AB∥DE，AC∥DF，
∴∠E＝∠B，∠DFE＝∠ACB，
∵BF＝EC，
∴BF+CF＝EC+CF，
即BC＝EF，
在△DEF和△ABC中，
，
∴△DEF≌△ABC（ASA），
∴DF＝AC．
四、（本大题共2小题，每小题8分，满分16分）
17．证明：∵OC＝PC，
∴∠P＝∠COP，
∵OA＝OC，
∴∠ACO＝∠CAO，
∵∠ACO是△PCO的一个外角，
∴∠ACO＝∠P+∠COP＝2∠P，
∴∠CAO＝∠ACO＝2∠P，
∵∠AOB是△PAO的一个外角，
∴∠AOB＝∠CAO+∠P＝3∠P，
∴∠APB＝∠AOB．
18．解：（1）如图所示，△A1B1C1即为所求，
其中A1的坐标为（﹣1，2），B1的坐标为（﹣3，0），C1的坐标为（﹣5，3）；
（2）△A1B1C1的面积＝3×4﹣×2×3﹣﹣＝12﹣3﹣2﹣2＝5．
五、（本大题共2小题，每小题10分，满分20分）
19．解：（1）根据点的坐标变化可知：
各点的坐标为：A5（2，﹣1），A9（4，﹣1），A13（6，﹣1），••••••
∴点A4n+1的坐标（n为正整数）为（2n，﹣1）；
故答案为：（2，﹣1），（4，﹣1），（6，﹣1），（2n，﹣1）；
（2）∵点A1到点A3的距离为1，点A1到点A5距离为2，点A1到点A7的距离为3，点A1到点A9的距离为4，••••••
∴点A1到点A2025的距离为（2025﹣1）÷2＝1012；
故答案为：1012．
20．解：（1）把C（2，2）代入y＝ax+4，得
2a+4＝2，
解得a＝﹣1，
把C（2，2）代入y＝kx，得
2k＝2，
解得k＝1；
（2）直线l1的解析式为y＝﹣x+4，直线l2的解析式为y＝x，
当y＝0时，﹣x+4＝0，
解得x＝4，
∴B点坐标为（4，0），
∴直线l1与l2与x轴围成的三角形面积＝×4×2＝4；
（3）结合图象，kx＞ax+4≥0的解集为2＜x≤4．
六、（本题满分12分）
21．证明：（1）∵△ADE和△ABC都是等边三角形，
∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，
∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，
即∠BAD＝∠CAE，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS）；
（2）∵△ABD≌△ACE，M，N分别是CE，BD的中点，
∴BD＝CE，AM＝AN，EM＝EC，DN＝BD，
∴EM＝DN，
在△AME和△AND中，
，
∴△AME≌△AND（SSS），
∴∠EAM＝∠DAN，
∴∠MAN＝∠DAM+∠DAN＝∠DAM+∠EAM＝∠DAE＝60°，
∴△AMN是等边三角形．
七、（本题满分12分）
22．解：（1）设篮球的单价为x元，排球的单价为y元，
由题意可得：，
解得，
答：篮球的单价为60元，排球的单价为50元；
（2）①由题意可得，
W＝60m+50（100﹣m）＝10m+5000，
∵每种球至少买一个且篮球个数不少于排球个数的3倍，
∴m≥1，m≥3（100﹣m），100﹣m≥1，
解得75≤m≤99，
即W关于m的函数表达式是W＝10m+5000（75≤m≤99）；
②∵W＝10m+5000，
∴W随m的增大而增大，
∵75≤m≤99，
∴当m＝75时，W取得最小值，此时W＝5750，100﹣m＝25，
即总费用最低的购买方案是购买篮球75个，排球25个，最低费用为5750元．
八、（本题满分14分）
23．（1）证明：∵∠ACB＝90°，
∴∠BCE+∠ACD＝90°，
∵AD⊥CE，
∴∠ACD+∠CAD＝90°，
∴∠BCE＝∠CAD，
∵AD⊥CE，BE⊥CE，
∴∠BEC＝∠ADC＝90°，
∵AC＝BC，
∴△ACD≌△CBE（AAS）；
（2）解：∵△ACD≌△CBE，
∴CE＝AD，BE＝CD，
∵AD＝6，BE＝2，
∴CD＝2，CE＝6，
∴DE＝CE﹣CD＝4；
（3）解：△DOE是等腰三角三角形，理由如下：
连接OC，设CE与AB的交点为M，
∵O是AB的中点，
∴OC＝AO＝OB，CO⊥AB，
∴∠MOC＝90°，
∵∠BME＝∠CMD，
∴∠EBM＝∠MCD，
∵CD＝BE，BO＝CO，
∴△BEO≌△CDO（SAS），
∴DO＝EO，∠BOE＝∠DOC，
∴∠COD+∠BOD＝∠BOE+∠DOM＝90°，
∴△DOE是等腰三角三角形．