安徽省阜阳市实验中学2024届九年级下学期周考数学试卷(含答案)

这是一份安徽省阜阳市实验中学2024届九年级下学期周考数学试卷(含答案)，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列函数是的二次函数的是（ ）
A．B．C．D．
2．如图，半径为5，那么图中到圆心距离为7的点可能是（ ）
A．点B．点C．点D．点
3．以原点为中心，将点按逆时针方向旋转，得到的点Q的坐标为（ ）
A．B．C．D．
4．阜合实验中学九年级进行拔河比赛，每个班级组成一队参赛，比赛采取单循环赛制（即每两队都要比赛一场），共比赛78场，则该校九年级班级数为（ ）
A．13B．12C．11D．10
5．已知四条线段a，b，c，d是成比例线段，其中，则线段a的长度为（ ）
A．8cmB．2cmC．4cmD．1cm
6．2023年12月13日，是我国第十个南京大屠杀死难者国家公祭日．某地从《南京！南京！》《东京审判》《屠城血证》三部影片中随机选取两部进行展播，则恰好展播《南京！南京！》《东京审判》的概率为（ ）
A．B．C．D．
7．如图，在每个小正方形边长为1的网格中，点A、B、C均落在格点上，用一个圆面去覆盖，则能够完全覆盖这个三角形的最小圆的半径为（ ）
A．B．2C．D．
8．已知A是双曲线y=在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为边作等边三角形ABC，点C在第四象限，已知点C的位置始终在一函数图象上运动，则这个函数解析式为（ ）
A．y=﹣B．y=﹣（x＞0）C．y=﹣6x（x＞0）D．y=6x（x＞0）
9．如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（ ）
A．1：3B．1：4C．2：3D．1：2
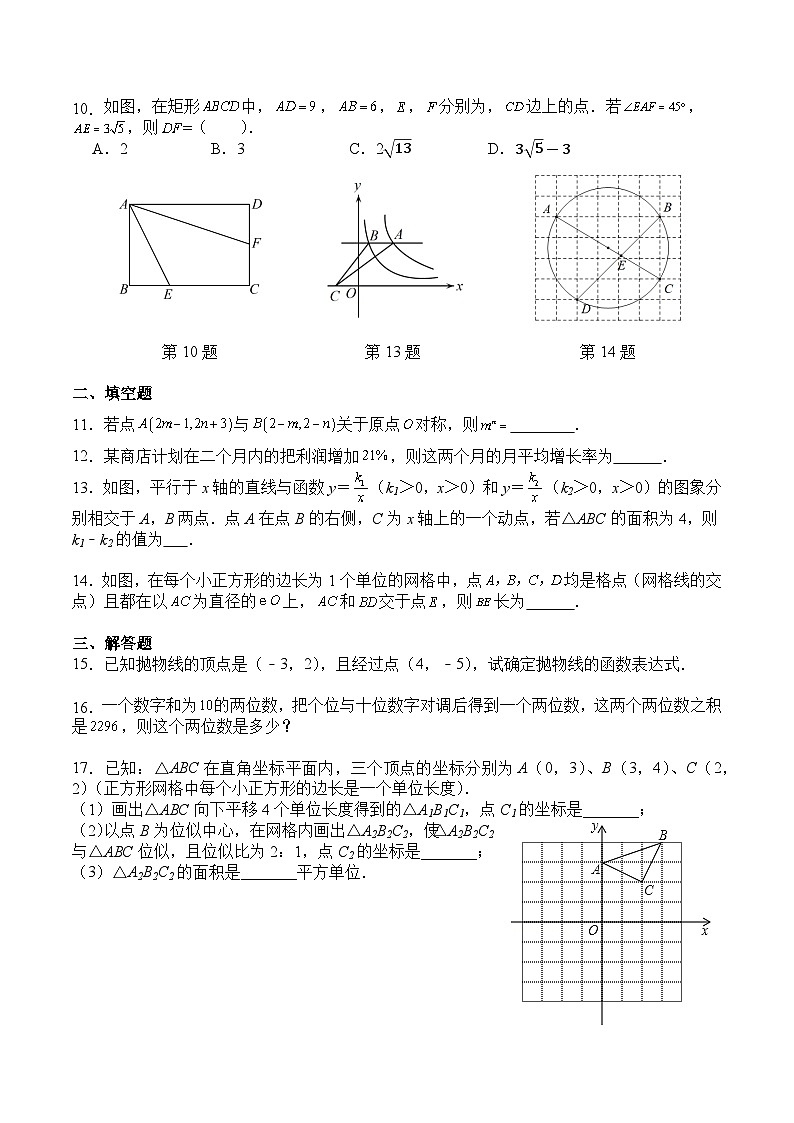
如图，在矩形中，，，，分别为，边上的点．若，，则=（ ）．
A．2B．3C．213D．35-3
二、填空题
11．若点与关于原点对称，则 ．
12．某商店计划在二个月内的把利润增加，则这两个月的月平均增长率为 ．
13．如图，平行于x轴的直线与函数y＝（k1＞0，x＞0）和y＝（k2＞0，x＞0）的图象分别相交于A，B两点．点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k1﹣k2的值为 ．
14．如图，在每个小正方形的边长为1个单位的网格中，点均是格点（网格线的交点）且都在以为直径的上，和交于点，则长为 ．
三、解答题
15．已知抛物线的顶点是（﹣3，2），且经过点（4，﹣5），试确定抛物线的函数表达式．
一个数字和为的两位数，把个位与十位数字对调后得到一个两位数，这两个两位数之积是，则这个两位数是多少？
17．已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是_______；
（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是_______；
（3）△A2B2C2的面积是_______平方单位．
18．已知反比例函数的图象经过第一、三象限．
(1)求的取值范围；
(2)若，此函数的图象过第一象限的两点，，且，求的取值范围．
19．如图，公园内有一个垂直于地面的立柱AB，其旁边有一个坡面，坡角．在阳光下，小明观察到在地面上的影长为，在坡面上的影长为．同一时刻，小明测得直立于地面长60cm的木杆的影长为90cm（其影子完全落在地面上）．求立柱AB的高度．

20．如图，在⊙中，是直径，点是⊙上一动点，连接,沿将翻折，交过点的切线于点，交⊙于点．

(1)求的度数；
(2)若半径为7，，求．
21．某初中学校举行毛笔书法大赛，对各年级同学的获奖情况进行了统计，并绘制了如下两幅不完整的统计图，请结合图中相关数据解答下列问题：
（1）求出一等奖人数，并将条形统计图补全；
（2）获得一等奖的同学中有来自七年级，有来自八年级，其他同学均来自九年级，现准备从获得一等奖的同学中任选两人参加市内毛笔书法大赛，请通过列表或画树状图求所选出的两人中既有七年级又有九年级同学的概率．
22．平面直角坐标系中，点O是坐标原点，抛物线 经过点 ，对称轴为直线．
(1)求、的值；
(2)抛物线与轴交于B、C两点（C在B的右侧），点D是抛物线的顶点,点E是抛物线上一动点，且位于直线的上方，过点E作的垂线交于点F，求长度的最大值.
23．如图1，点在正方形的对角线上，正方形的边长是，的两条直角边分别交边于点．

（1）操作发现：如图2，固定点，使绕点旋转，当时，四边形是正方形．
填空：①当时，四边形的边长是_____；
②当（是正实数）时，四边形的面积是______；
（2）猜想论证：如图3，将四边形的形状改变为矩形，，，点在矩形的对角线，的两条直角边分别交边于点，固定点，使绕点旋转，则______；
（3）拓展探究：如图4，当四边形满足条件：，，时，点在对角线上，分别交边于点，固定点，使绕点旋转，请探究的值，并说明理由．
第2题
第7题
第8题
第9题
第10题
第13题
第14题
参考答案：
1．C
2．D
3．C
4．A
6．B
7．C
8．B
9．D
10．B
11．
12．
13．8
14．
15．抛物线的表达式为y=−（x+3）2+2．
16．或
17．（1）（2，﹣2）；
（2）（1，0）；
（3）10．
解析：（1）如图所示：C1（2，﹣2）；
故答案为（2，﹣2）；
（2）如图所示：C2（1，0）；
故答案为（1，0）；
（3）∵，，，
∴△A2B2C2是等腰直角三角形，
∴△A2B2C2的面积是：（平方单位）．
故答案为10．
18．(1)
(2)
（1）解：由题意知，，
解得，，
∴的取值范围为；
（2）解：由题意知，反比例函数在第一象限，随着的增大而减小，
∵，
∴，解得，，
∵，
∴，
∴的取值范围为．
19．(170+60)cm
解：延长AD交BN于点E，过点D作DF⊥BN于点F，

在Rt△CDF中，∠CFD=90°，∠DCF=30°，
则DF=CD=90（cm），CF=CD•cs∠DCF=180×=90（cm），
由题意得：=，即=，
解得：EF=135，
∴BE=BC+CF+EF=120+90+135=(255+90)cm，
则=，
解得：AB=170+60，
答：立柱AB的高度为(170+60)cm．
20．(1)
(2)
（1）解：如图所示，连接，

∵
∴，
∵折叠，
∴，
∴
∴
∵是的切线，
∴，
∴
（2）解：如图所示，过点作于点，

∵，
∴，
∴，
∵半径为7，，
∴，
则，
在中，，
∴
21．（1）补图见解析；（2） ．
（1）调查的总人数为10÷25%=40（人），
∴获一等奖人数：40-8-6-12-10=4（人），
补全条形图如图所示：
（2）七年级获一等奖人数：4×=1（人），
八年级获一等奖人数：4×=1（人），
∴ 九年级获一等奖人数：4-1-1=2（人），
七年级获一等奖的同学用M表示，八年级获一等奖的同学用N表示，
九年级获一等奖的同学用P1、P2表示，树状图如下：
共有12种等可能结果，其中获得一等奖的既有七年级又有九年级人数的结果有4种，
所以所选出的两人中既有七年级又有九年级同学的概率P=．
22．(1)，
(2)(ⅰ) (ii)或
（1）解：由题意得
，
解得：，
答：，；
（2）解：（ⅰ）如图，过作轴，交轴于，交直线于，

，
，
，
，
由（1）得
，
当时，，
解得：，，
，
设直线的解析式为，则有
，
解得：，
直线的解析式为，
设，
，，
，
，，
，
，
()，
，
；
故长度的最大值．
（ii）①如图，取的中点，过作交于，连接、，过作轴交于，

，，
，
，
即：，
是抛物线的顶点，
当时，
，
，
，
，
，
，
，，，
，
为直角三角形，
，
，
，
，
，
解得：，
，，
，
，
，
，
，
解得：，
，
；
②如图，作线段关于对称的线段交直线于，

，
，
，
设，
，
整理得：，
解得：，，
当时，，
不合题意，舍去，
，
，
；
故的坐标或．
23．（1）①；②；（2）；（3），理由见解析
解析：（1）①
，，，，，，，，即，，
∵四边形是正方形，∴四边形的边长是．
②
当时，，，，∴四边形的面积为．
（2）
如图，

过点作于点，于点，则，，又，，，．由，，得，，，，即，．
（3）．理由如下：

如图，过点作交于点，交于点，则，
，，
即，
，
，，
又，，
，．
由，，得，，
，
即，．