人教版（2024）七年级上册（2024）5.1 方程习题ppt课件

这是一份人教版（2024）七年级上册（2024）5.1 方程习题ppt课件，文件包含人教版七年级上册数学511从算式到方程pptx、人教版七年级上册数学511《从算式到方程》教案docx、人教版七年级上册数学511《从算式到方程》分层练习docx、人教版七年级上册数学511《从算式到方程》预习案docx等4份课件配套教学资源，其中PPT共53页， 欢迎下载使用。
新课标着重对学生核心素养的培养，培养学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界会用方程描述现实问题中的数量关系和变化规律形成合适的运算思路解决问题；形成抽象能力、模型观念，进一步发展运算能力.
方程是重要的数学基本概念，它随着实践需要而产生，具有极其广泛的应用，是刻画现实世界的一种有效的数学模型. 本章上承有理数、整式的加减，下启其它代数方程(组)，不等式函数等知识.一元一次方程是最简单、最基本的方程，从解法来看，任何一个代数方程(组)最终都化归为一元一次方程来解.
本章让学生的运算能力进一步提升，从解决实际问题来看，本章让学生经历完整的用方程模型解决实际问题的全过程，使学生数学建模能力得到进一步发展为列二元一次方程组，一元二次方程，函数解析式，不等式解决实际问题，打好坚实基础.
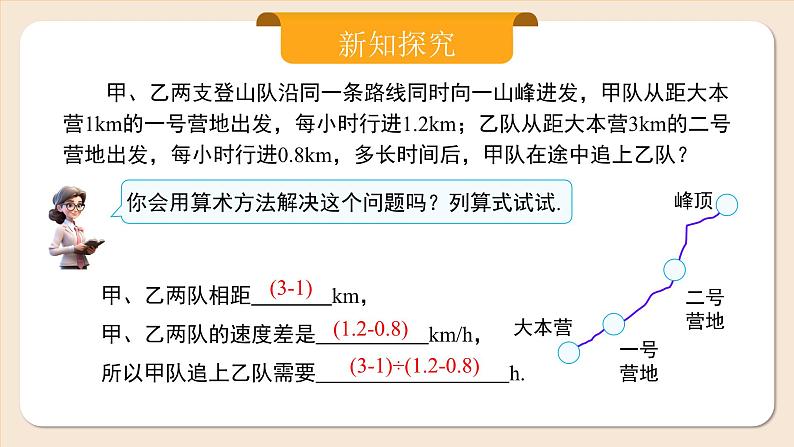
甲、乙两支登山队沿同一条路线同时向一山峰进发，甲队从距大本营1km的一号营地出发，每小时行进1.2km；乙队从距大本营3km的二号营地出发，每小时行进0.8km,多长时间后，甲队在途中追上乙队？
你能用小学学过的算术方法解决这个问题吗？ 本章我们将学习一种新的方法，通过列方程来解决这个问题.方程是含有未知数的等式，它是应用广泛的数学工具，解决许多实际问题时，人们经常用字母表示其中的未知数，通过分析问题中的数量关系，列出方程表示相等关系，然后解方程求出未知数，从而获得实际问题的答案.
怎样根据问题中的数量关系列方程？怎样解方程？这是本章研究的主要问题. 通过学习本章中丰富多彩的问题，你将初步感受方程的作用，并学习利用一元一次方程解决问题的方法.
1．让学生在掌握算式和简单方程的基础上，过渡到一元一次方程的学习；
4．掌握一元一次方程的概念，会判断所给方程是否为一元一次方程.
3．掌握方程的解的概念，会判断方程的解；
2．理解方程的意义，会根据实际情境列方程；
甲、乙两支登山队沿同一条路线同时向一山峰进发，甲队从距大本营1km的一号营地出发，每小时行进1.2km；乙队从距大本营3km的二号营地出发，每小时行进0.8km，多长时间后，甲队在途中追上乙队？
甲、乙两队相距 km，甲、乙两队的速度差是 km/h，所以甲队追上乙队需要 h.
(3-1)÷(1.2-0.8)
思考：在这个问题中，已知： .未知： .
甲乙两队的行进速度及甲乙两队到大本营的距离
如果设两队的行进时间为x h，根据“路程=速度×时间”，甲队和乙队行进路程可以分别表示为1.2x km和0.8x km.
甲队(1.2km/h)
乙队(0.8km/h)
乙队距大本营的路程：(0.8x+3)km
甲队距大本营的路程：(1.2x+1)km
想一想，甲队追上乙队时，他们距大本营的路程之间有什么关系？
(1.2x+1)km= (0.8x+3)km
甲队距大本营的路程 = 乙队距大本营的路程
问题1 用买12个大水杯的钱，可以买16个小水杯，大水杯的单价比小水杯的单价多5元，两种水杯的单价各是多少元？
思考：本题的等量关系是什么？
设大水杯的单价为x元，那么小水杯的单价为(x-5)元.
买12个大水杯的钱 = 买16个小水杯的钱
根据“单价×数量=总价”，可以列方程
12x = 16(x-5).
由这个含有未知数x的等式可以求出大水杯的单价，进而可以求出小水杯的单价.
思考：若将小水杯的单价设为x元？你会列方程吗？
设小水杯的单价为x元，那么大水杯的单价为 元.
12(x+5) =16x.
由这个含有未知数x的等式可以求出小水杯的单价，进而可以求出大水杯的单价.
由这个含有未知数x的等式可以求出这枚纪念币的长，进而可以求出纪念币的宽.
0.8x+3 = 1.2x+1
注意：方程必须满足两个条件：(1)是等式；(2)化简后含有未知数. 二者缺一不可.
3. 判断下列各式哪些是方程？是的标记“√”，不是的标记“×”.
用算术方法解题时，列出的算式表示用算术方法解题的计算过程，其中只含有已知数，不含未知数； 而方程是根据问题中的相等关系列出的等式，其中既含有已知数，也含有用字母表示的未知数，这为解决许多问题带来了方便. 通过今后的学习，你会逐步认识到：从算式到方程是数学的一大进步.
例1 根据下列问题，设未知数并列出方程：(1) 某校女生占全体学生数的52%，比男生多80人，这所学校有多少名学生？
解：设这所学校的学生数为x，那么女生数为0.52x，男生数为(1-0.52)x，根据“女生比男生多80人”，列得方程0.52x - (1-0.52)x = 80.
女生人数-男生人数=80.
例1 根据下列问题，设未知数并列出方程：(2) 如图，一块正方形绿地沿某一方向加宽5m，扩大后的绿地面积是500m2，求正方形绿地的边长.
解：设正方形绿地的边长为x m，依据
扩大后的绿地面积= 500m2
1.《算法统宗》是我国古代数学著作，其中记载了一道数学问题,大意如下：用绳子测水井深度，若将绳子折成三等份，则井外余绳4尺；若将绳子折成四等份，则井外余绳 1尺.问绳长和井深各多少尺？设井深为x尺，则可列方程为 .
解析：根据将绳三折测之，绳多四尺，则绳长为：3(x+4)； 根据绳四折测之，绳多一尺，则绳长为：4(x+1). 故3(x+4)=4(x+1)．
3(x+4)=4(x+1)
2.甲、乙两人分别从相距30千米的A，B两地骑车相向而行，甲骑车的速度是 10千米/时，乙骑车的速度是8千米/时，甲先出发25分钟后，乙骑车出发，问乙出发后多少小时两人相遇？(只列方程)莉莉：设乙出发后x小时两人相遇，列出的方程为25×10+8x+10x=30.请问莉莉列出的方程正确吗？如果不正确，请说明理由并列出正确的方程.
归纳 分析实际问题中的数量关系，利用其中的相等关系列出方程，是用数学解决实际问题的一种方法. 这个过程可以表示如下：
列方程的基本思路： (1)理解题意，弄清已知是什么，未知是什么； (2)找出题目中的相等关系； (3)根据相等关系列方程。
准确找出相等关系是列方程的关键，一般可以从以下几个方面入手：(1) 根据周长、面积、体积等公式列方程；(2) 根据题目中的不变量确定相等关系；(3) 根据关键词确定相等关系，如和差关系通常用“一共有……”、“比……多………”、“比……少……”表示，倍数关系通常用“是……的几倍”表示.
根据下列问题，设未知数并列出方程：1.甲种铅笔每支1.4元，乙种铅笔每支1.8元，用23元钱买这两种铅笔一共买了15支，两种铅笔各买了多少支？2.有两条电线，第一条长90m，第二条长40 m.要从第一条截下一段接在第二条上，使两条电线长度相等求截下的那段电线的长度(两条电线接头部分的长度忽略不计).
解：设买甲种铅笔x支，则有1.4x+1.8(15-x)=23.
解：设截下x m，则有90-x=40+x.
根据下列问题，设未知数并列出方程：3.某圆环形状的工件如图所示，它的面积是200cm2，外沿大圆的半径是10cm，内沿小圆的半径是多少厘米?
解：设內沿小圆半径为x cm，则有等量关系： 大圆面积-小圆面积=200 可以列方程：π×102-πx2 = 200
列方程是解决实际问题的重要方法，要想得到实际问题的解，还需要求出方程中未知数的值.
1.2x+1= 0.8x+3
当x=4时，方程左边：1.2×4+1=5.8；方程右边：0.8×4+3=6.2.
当x=5时，方程左边：1.2×5+1=7；方程右边：0.8×5+3=7.
当x=6时，方程左边：1.2×6+1=8.2；方程右边：0.8×6+3=7.8.
可以发现只有当x=5时，方程左、右两边的值相等.
一般地，使方程左、右两边的值相的未知数的，叫作方程的解(slu-tin).例如，x=5就是方程 1.2x+1=0.8x+3的解. 求方程的解的过程，叫作解方程。
方程的解与解方程的区别与联系
例2 (2) x=10，x=20是方程12x=16(x-5)的解吗？
解：当x=10时， 方程12x=16(x-5)的左边=12×10=120，右边=16 ×(10-5)=80，方程左、右两边的值不相等，所以x=10不是方程12x=16(x-5)的解. 当x=20时， 方程12x=16(x-5)的左边=12×20=240，右边=16×(20-5)=240，方程左、右两边的值相等，所以x=20是方程12x=16(x-5)的解.
将数值代入方程左边进行计算；
将数值代入方程右边进行计算.
若左边＝右边，则是方程的解，若左边≠右边，则不是方程的解.
共同特征：1. 只含有一个未知数；2. 未知数的次数是1；3. 方程两边都是整式.
一般地，如果方程中只含有一个未知数(元)，且含有未知数的式子都是整式，未知数的次数都是1，这样的方程叫作一元一次方程.
一元一次方程的三个特征： 1.只含有一个未知数； 2.等式两边都是整式； 3.未知数的次数都是1.
符合一元一次方程的概念
化简后符合一元一次方程的概念
等号左边分母含有未知数，不是整式
1. 判断x=2和x=4是不是方程2x-3=5 的解.
2. 下列等式中哪些是方程？哪些是一元一次方程？ ①2+3=3+2；②8y-9=9-y； ③ x2+2x+1＝4．
解： ② ③为方程； ②为一元一次方程.
解：当x=2时，方程左边=2×2-3=1，方程右边=5；因为左边≠右边，所以x=2不是方程2x-3=5的解. 当x=4时，方程左边=2×4-3=5，方程右边=5；因为左边=右边，所以x=4是方程2x-3=5的解.
2. 若 x =1是方程x2 -2mx +1=0的一个解，则m的值为( )A. 0 B. 2 C. 1 D. -1
3.下列各式中，是方程的是( )A.4-5=-1 B.x+3y-1 C.s+2t=-5 D.a-6