初中人教版（2024）5.2 解一元一次方程习题ppt课件

这是一份初中人教版（2024）5.2 解一元一次方程习题ppt课件，文件包含人教版七年级上册数学522《移项》pptx、人教版七年级上册数学522《用移项法解一元一次方程》教案docx、人教版七年级上册数学522《用移项法解一元一次方程》分层练习docx、人教版七年级上册数学522《用移项法解一元一次方程》预习案docx等4份课件配套教学资源，其中PPT共33页， 欢迎下载使用。

2.学会运用移项解形如“ax+b=cx+d”的一元一次方程；
1.理解移项的意义，掌握移项的方法；
3.能够抓住实际问题中的数量关系列一元一次方程解决实际问题.
2. 观察下列一元一次方程，与上题的类型有什么区别？
怎样才能使它向 x=a (a为常数)的形式转化呢？
系数化为1，得x = 4
3x ＋7=32 －2x
问题2 把一批图书分给某班学生阅读，若每人分3本，则剩余20本；若每人分4本，则缺25本，这个班有多少名学生？
这批书的总数是一个定值，表示它的两个式子应相等，根据这一相等关系列得方程3x+20=4x-25.
设这个班有x名学生.每人分3本，共分出3x本，加上剩余的20本，这批书共(3x+20)本.每人分4本，需要4x本，减去缺的25本，这批书共(4x-25)本.
这批书的总数有几种表示方法？它们之间有什么关系？
“表示同一个量的两个不同的式子相等”是一个基本的相等关系.
3x+20=4x-25
3x-4x=-25-20
为了使方程的右边没有含x的项，等式两边减4x，利用等式的性质1，得
3x+20-4x=-25
为了使方程的左边没有常数项，等式两边减20，利用等式的性质1，得
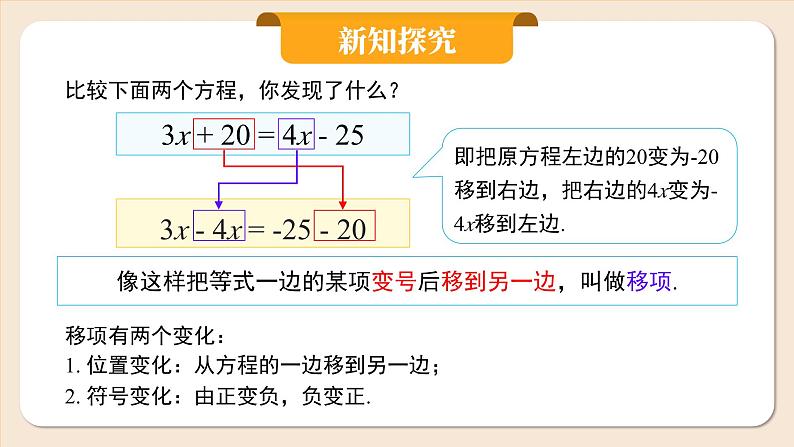
比较下面两个方程，你发现了什么？
3x + 20 = 4x - 25
3x - 4x = -25 - 20
像这样把等式一边的某项变号后移到另一边，叫做移项.
即把原方程左边的20变为-20移到右边，把右边的4x变为-4x移到左边.
移项有两个变化：1. 位置变化：从方程的一边移到另一边；2. 符号变化：由正变负，负变正.
由上可知，这个班有45名学生.
移项的依据：等式的性质1.
移项的作用：通过移项，将含有未知数的项与常数项分别移到方程的两边，使方程更接近于ax=b(a≠0)的形式.
例3 解下列方程：
解：(1)移项，得 3x+2x=32-7.合并同类项，得 5x=25.系数化为1，得 x=5.
(1) 3x+7=32-2x；
移项解一元一次方程的步骤：
1.解方程5x-3=2x+2，移项正确的是( )A.5x-2x=2+3 B.5x+2x=2+3 C.5x-2x=2-3 D.5x+2x=2-32.若x的2倍与8的和等于6与x的2倍的差，则x= .3.当：x= 时，2x-3与3x+1的值互为相反数. 4.若单项式-2a3b2n-1与am-1b3n+2的和仍是单项式，则m+n= .
解：(1)移项，得 3x+5x=6-4 合并同类项，得 2x=2. 系数化为1，得 x=1.
(2)移项，得2.5m+10m-6m=-21.5+15.合并同类项，得 6.5m=-6.5.系数化为1，得 m=-1.
例4 某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多200t；如用新工艺，则废水排量比环保限制的最大量少100t.新、旧工艺的废水排量之比为2:5，采用两种工艺的废水排量各是多少吨?
旧工艺：废水排量=环保限制的最大量+200
新工艺：废水排量=环保限制的最大量-100
环保限制的最大量=旧工艺废水排量-200
环保限制的最大量=新工艺废水排量+100
解：设采用新、旧工艺的废水排量分别为 2x t和5x t.得5x-200=2x+100.移项，得5x-2x=100+200.合并同类项，得3x=300.系数化为1，得x=100.所以2x=200，5x=500.答：采用新、旧工艺的废水排量分别为200t和500t.
旧工艺废水排量-200 =新工艺废水排量+100
1.甲仓库有200t煤，乙仓库有80t煤，若甲仓库每天运出15t煤，乙仓库每天运进25t煤，则 天后两仓库存煤量相等.2.《九章算术》中有一个“盈不足术”的问题，其大意是：若干人共同出资买羊，每人出5钱，则差45钱；每人出7钱，则差3钱.问：人数和羊价各是多少？
解：设人数为x.根据题意，有5x+45=7x+3.移项，得5x-7x=3-45.合并同类项，得-2x=-42.系数化为1，得x=21.所以5x+45=150.答：人数为21,羊价为150钱.
3.我区期末考试一次数学阅卷中，阅B卷第28题(简称B28)的教师人数是阅A卷第18题(简称A18)教师人数的3倍，在阅卷过程中，由于情况变化，需要从阅B28题中调12人到A18阅卷，调动后阅B28剩下的人数比原先阅A18人数的一半还多3人，求阅B28题和阅A18题的原有教师人数各为多少？
调动前：阅B28题的教师人数=3×阅A18题的教师人数
调动后：阅B28题的教师人数－12=原阅A18题的教师人数÷2+3
解：设原有教师x人阅A18题，则原有教师3x人阅B28题，
答：阅A18题原有教师6人，阅B28题原有教师18人.
系数化为1，得 x = 6，
4.下面是两种移动电话计费方式：
问：一个月内，通话时间是多少分钟时，两种移动电话计费方式的费用一样？
解：设通话时间t分钟，则按方式一要收费(50+0.3t)元，
按方式二要收费(10＋0.4t).
如果两种移动电话计费方式的费用一样，
则 50+0.3t＝ 10＋0.4t.
移项，得 0.3t－ 0.4t =10－50.
合并同类项，得 －0.1t =－40.
系数化为1，得 t =400.
答：一个月内通话400分钟时，两种计费方式的费用一样.
解：(1) x = -3；(2) x = 4；(3) y =1； (4) y = -24.
解：移项，得1.2x- 0.8x =3-1. 合并同类项，得0.4x=2. 系数化为1，得x=5.
3.李明出生时父亲28岁，现在父亲的年龄是李明年龄的3倍，求现在李明的年龄. 4.王芳和张华同时采摘樱桃，王芳平均每小时采摘8kg，张华平均每小时采摘7kg.采摘结来后王芳从她采摘的樱桃中取出0.25 kg给了张华，这时两人的樱桃一样多，她们采摘用了多长时间?
解：设现在李明的年龄为x岁，根据题意，得3x=28+x.解得x=14.答：现在李明年龄为14岁.
解：设她们采摘用了x h，根据题意，得8x-0.25=7x+0.25，解得x=0.5.答：她们采摘用了0.5h.
1. 通过移项将下列方程变形，正确的是 ( )A. 由5x－7＝2，得5x＝2－7B. 由6x－3＝x＋4，得3－6x＝4＋xC. 由8－x＝x－5，得－x－x＝－5－8D. 由x＋9＝3x－1，得3x－x＝－1＋9
2. 已知 2m－3=3n+1，则 2m－3n =______.
2m－3n = 3+1
4. 当x =_____时，式子 2x－1 的值比式子 5x+6 的值小1.
2x－1 ＝5x+6－1
2x－5x＝1+6－1
5. 解下列一元一次方程：
答案：(1) x =－2； (2) t =20； (3) x =－4； (4) x =2.
(1) 7 －2x =3 －4x
(2) 1.8t =30 ＋ 0.3t
6. 小明和小刚每天早晨坚持跑步，小明每秒跑4 米，小刚每秒跑6米. 若小明站在百米起点处，小刚站在他前面10米处，两人同时同向起跑，几秒后小明追上小刚？
解：设小明x秒后追上小刚，
可得方程： 4x＋10＝6x.
移项，得 4x－6x＝－10.
合并同类项，得 －2x＝－10.
系数化为1，得 x＝5.
答：小明5秒后追上小刚.
注意：移项一定要变号.
把等式一边的某项变号后移到另一边，叫做移项.