

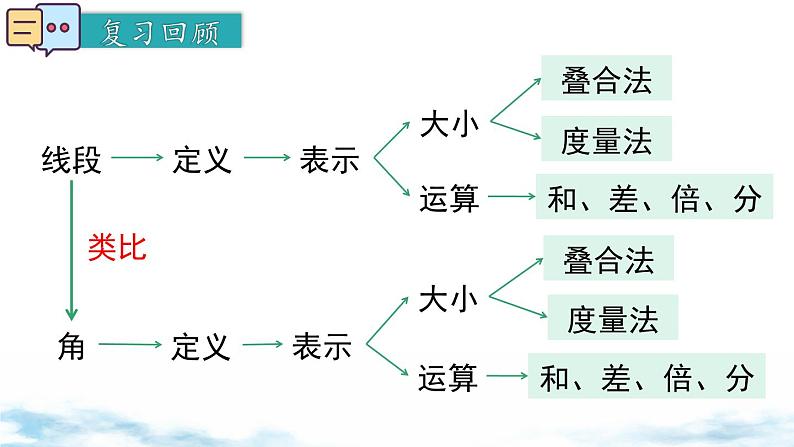


所属成套资源:北师大版(2024)七年级上册数学同步课件
初中数学2 角完整版备课ppt课件
展开
这是一份初中数学2 角完整版备课ppt课件,共22页。PPT课件主要包含了度量法,叠合法,∠BOC>∠DOE,小亮用的是叠合法,∠AOB,∠BOC,∠AOC,对折法,几何语言,∠AOB15°等内容,欢迎下载使用。
1. 经历比较角的大小的研究过程,体会角的大小比较和线段的长短比较方法的一致性。2. 通过让学生亲自动手演示比较角的大小,让学生经历 “观察一对比一归纳”的学习过程,并培养学生的动手操作能力及类比的数学思想。重点:比较角的大小,认识角的平分线,作一个角等于 知角。难点:角的平分线的应用。
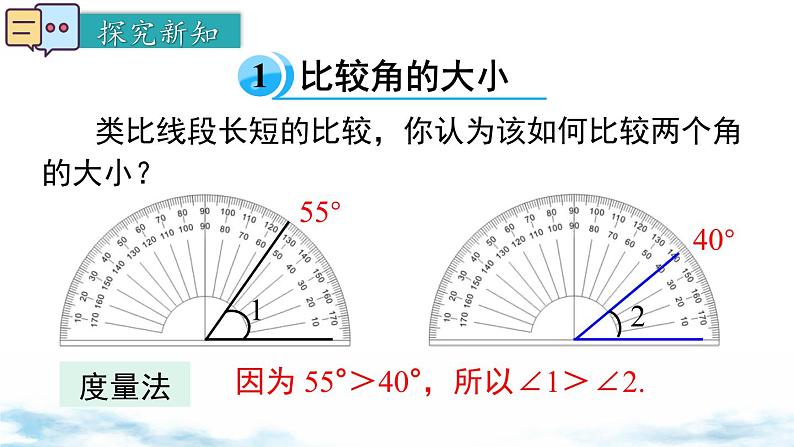
类比线段长短的比较,你认为该如何比较两个角的大小?
因为 55°>40°,所以∠1>∠2.
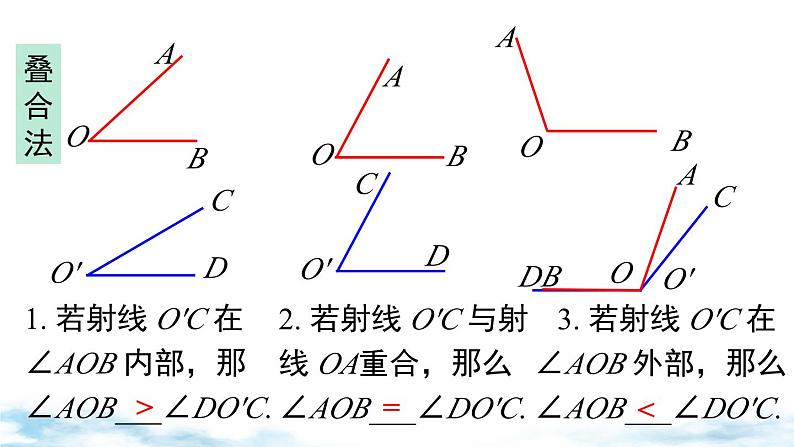
2. 若射线 O'C 与射线 OA重合,那么∠AOB___∠DO'C.
1. 若射线 O'C 在∠AOB 内部,那∠AOB___∠DO'C.
3. 若射线 O'C 在∠AOB 外部,那么∠AOB___∠DO'C.
1. 角的大小与两边画出部分的长短是否相关?
2. 一个 30° 的角用能放大 3 倍的放大镜观看,看到的角度有何变化?
角的大小与两边画出部分的长短无关.
根据右图求解下列问题:
(1)比较 ∠AOB,∠AOC,∠AOD,∠AOE 的大小,并指出其中的锐角、直角、钝角、平角.
∠AOB<∠AOC<∠AOD<∠AOE
∠AOB是锐角,∠AOC是直角,∠AOD是钝角,∠AOE是平角.
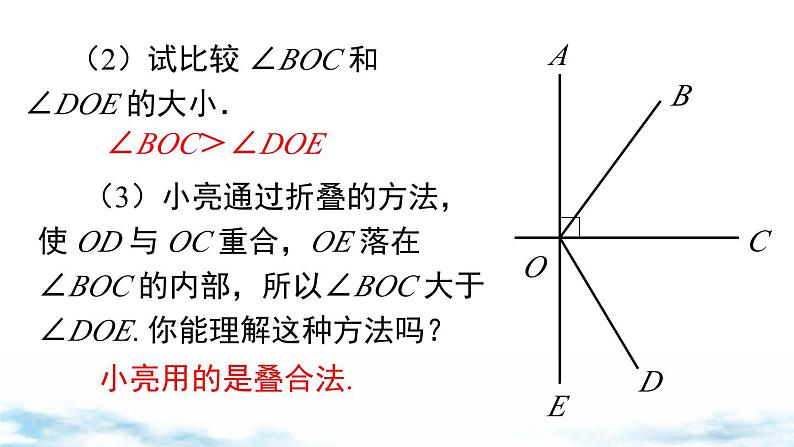
(2)试比较 ∠BOC 和 ∠DOE 的大小.
(3)小亮通过折叠的方法,使 OD 与 OC 重合,OE 落在 ∠BOC 的内部,所以∠BOC 大于 ∠DOE. 你能理解这种方法吗?
(4)请在图中画出小亮折叠的折痕 OF,∠DOF 与∠COF 有什么大小关系?
∠DOF = ∠COF
探究1:如图,图中共有几个角?它们之间有什么关系?
∠AOC = ∠AOB + ∠BOC
∠AOB = ∠AOC - ∠BOC
∠BOC = ∠AOC - ∠AOB
探究2 :如图,借助三角尺画出 15°,75° 的角.用一副三角尺,你还能画出哪些度数的角?试一试.
还能画出 105°、120°、150°、180° 的角.
例1 如图,O 是直线 AB 上一点,∠AOC = 53°,求∠BOC 的度数.
解:由题意可知,∠AOB 是平角,∠AOB =∠AOC +∠BOC.所以∠BOC =∠AOB -∠AOC = 180° - 53°= 127°.
1. 如图,已知点 O 为直线 AB 上一点,∠DOC = 18°,∠AOD = 102°,求∠BOC 的大小.
解:由题意可知,∠AOB 是平角,
= 180° - 102° = 78° ,
所以∠BOD =∠AOB -∠AOD
∠AOB =∠AOD +∠BOD.
∠BOC =∠BOD +∠DOC
= 78° + 18° = 96°.
探究3:你能在∠AOC 内找一条射线 OB,使∠AOB =∠BOC 吗?
此时 ∠AOC = 2∠AOB = 2, ∠AOB =∠BOC = .
2. 如图,∠AOB=90°,OE,OC 分别是∠AOD,∠DOB 的平分线,则∠EOC=________°.
类比:仿照角平分线的结论,你能写出角的三等分线的结论吗?
因为射线 OB、OC 是 ∠AOD 的三等分线,所以
例2 如图 ,OC 是∠AOB 的平分线,OB 是∠COD 的三等平分线,∠BOD = 15°, 则∠AOB 等于 ( ).A. 75°B. 70°C. 65°D. 60°
思考:除此题所给图片的情况,你还能想出其他情况与答案吗?
从一个角的 引出的一条射线,把这个角分成两个 的角,这条射线叫作这个角的平分线
1. 如图:已知∠1 = ∠3,那么( )A.∠1 = ∠2 B. ∠2 = ∠3 C.∠AOC = ∠BOD D. ∠1 =
2. 如图所示,已知直线 AB,CD 相交于点 O,OA 平分∠EOC,∠EOC=70°,则∠BOD 等于( )A.30° B.35°C.20° D.40°
相关课件
这是一份北师大版(2024)七年级上册(2024)2 角精品备课课件ppt,共13页。PPT课件主要包含了作法一等内容,欢迎下载使用。
这是一份初中北师大版(2024)2 角优秀备课课件ppt,共24页。PPT课件主要包含了探究1,并说出它们是什么角,∠AOB,∠BOA,用一个数字表示,∠BAC,∠CAD,∠BAD,量角器,角的度量工具等内容,欢迎下载使用。
这是一份初中数学北师大版(2024)七年级上册(2024)1 代数式评优课备课课件ppt,共20页。PPT课件主要包含了游戏比拼,x+1,x+12,张老师体重适中,在代入数值时应注意,逐渐增大,n2先超过,代数式的值,代入求值,基础练习等内容,欢迎下载使用。











