

数学-吉林省通化市梅河口市第五中学2025届高三9月月考
展开
这是一份数学-吉林省通化市梅河口市第五中学2025届高三9月月考,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
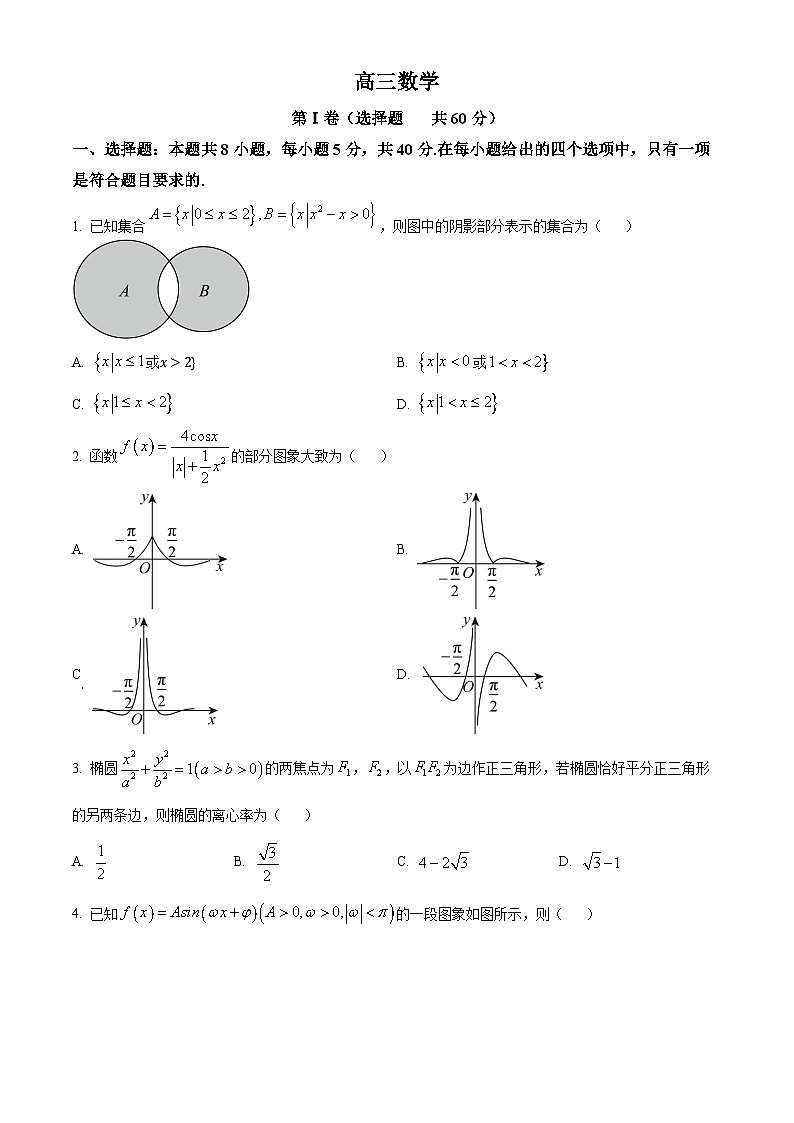
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则图中的阴影部分表示的集合为( )
A. 或x>2B. 或
C. D.
2. 函数的部分图象大致为( )
A. B.
C D.
3. 椭圆的两焦点为,,以为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为( )
A. B. C. D.
4. 已知的一段图象如图所示,则( )
A.
B. 的图象的一个对称中心为
C. 的单调递增区间是
D. 函数的图象向左平移个单位后得到的是一个奇函数的图象
5. 用一个边长为4正方形纸片,做一个如图所示的几何体,图中两个圆锥等底、等高,则该几何体体积的最大值为( )
A. B. C. D.
6. 若,则的大小关系为( )
A. B. C. D.
7. 元旦联欢会会场中挂着如图所示的两串灯笼, 每次随机选取其中一串并摘下其最下方的一个灯笺, 直至某一串灯笼被摘完为止, 则右侧灯笼先被摘完的概率为( )
A. B. C. D.
8. 如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或向上或右下移动,而一条移动路线由若干次移动构成,如从1移动到11:1→2→3→5→7→8→9→10→11就是一条移动路线.从1移动到数字的不同路线条数记为,从1移动到11的事件中,跳过数字的概率记为,则下列结论正确的是( )
①,②,③,④.
A. ①②③B. ①②④C. ②③④D. ①②③④
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9 已知函数,则( )
A. 的图象关于直线对称
B. 的图象关于点对称
C. 在区间上单调递减
D. 在区间的值域为
10. 已知点为抛物线焦点,为上不重合的两个动点,为坐标原点,若直线(直线斜率存在且不为0)与仅有唯一交点,则( )
A. 的准线方程为
B. 若线段与的交点恰好为中点,则
C. 直线与直线垂直
D. 若,则
11. 如图所示曲线被称为双纽线,该种曲线在生活中应用非常广泛,其代数形式可表示为坐标中(为坐标原点)动点到点的距离满足:,则( )
A. OP的最大值是
B. 若是曲线上一点,且在第一象限,则
C. 与有1个交点
D. 面积的最大值是
三、填空题(本题共3小题,每小题5分,共15分)
12. 设抛物线的焦点为,过点作直线交抛物线于,两点,若,,则___________.
13. 若曲线在点处的切线与曲线相切,则________.
14. 某射击比赛中,甲、乙两名选手进行多轮射击对决.每轮射击中,甲命中目标的概率为,乙命中目标的概率为.若每轮射击中,命中目标的选手得1分,未命中目标的选手得0分,且各轮射击结果相互独立.则进行五轮射击后,甲的总得分不小于3的概率为__________.
四、解答题: 本题共 5 小题. 解答应写出文字说明、证明过程或演算步骤.
15. 在中,a,b,c分别为角A,B,C的对边,已知,且.
(1)求角A的大小;
(2)求面积的最大值.
16. 已知数列{an}的前n项和为Sn,a1=2,an+1=2Sn+2.
(1)求数列{an}的通项公式;
(2)若2bn=3nan,求数列{bn}的前n项和Tn.
17. 在中,角的对边分别为的面积为,已知.
(1)求角;
(2)若的周长为,求的最大值.
18. 正四棱柱中,点分别在上,且四点共面.
(1)若,记平面与底面的交线为,证明:;
(2)已知,若,求四边形面积的最大值.
19. 在高中数学教材苏教版选择性必修2上阐述了这样一个问题:假设某种细胞分裂(每次分裂都是一个细胞分裂成两个)和死亡的概率相同,如果一个种群从这样的一个细胞开始变化,那么这个种群最终灭绝的概率是多少?在解决这个问题时,我们可以设一个种群由一个细胞开始,最终灭绝的概率为,则从一个细胞开始,它有的概率分裂成两个细胞,在这两个细胞中,每个细胞灭绝的概率都是,两个细胞最终都走向灭绝的概率就是,于是我们得到:,计算可得;我们也可以设一个种群由一个细胞开始,最终繁衍下去的概率为,那么从一个细胞开始,它有的概率分裂成两个细胞,在这两个细胞中,每个细胞繁衍下去的概率都是,两个细胞最终都走向灭绝的概率就是,于是我们得到:,计算可得.根据以上材料,思考下述问题:一个人站在平面直角坐标系的点处,他每步走动都会有的概率向左移动1个单位,有的概率向右移动一个单位,原点处有一个陷阱,若掉入陷阱就会停止走动,以代表当这个人由开始,最终掉入陷阱的概率.
(1)若这个人开始时位于点处,且.
(ⅰ)求他在5步内(包括5步)掉入陷阱的概率;
(ⅱ)求他最终掉入陷阱的概率;
(ⅲ)已知,若,求;
(2)已知是关于的连续函数.
(ⅰ)分别写出当和时,的值(直接写出即可,不必说明理由);
(ⅱ)求关于的表达式.
高三数学
第Ⅰ卷(选择题 共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则图中的阴影部分表示的集合为( )
A. 或x>2B. 或
C. D.
【答案】A
【解析】
【分析】由题可知图中的阴影部分表示,再根据交集,并集和补集的定义即可得解.
【详解】由题可知图中的阴影部分表示,
或,
则,
所以或x>2.
故选:A.
2. 函数的部分图象大致为( )
A. B.
C. D.
【答案】C
【解析】
【分析】利用奇偶性的定义确定函数为偶函数,再根据余弦函数的性质可求解.
【详解】由题可知,的定义域为,
又因为,
所以,为偶函数.
当时,,当时,,当时,.
故选:C.
3. 椭圆的两焦点为,,以为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为( )
A. B. C. D.
【答案】D
【解析】
【分析】设椭圆与正三角形另两条边的交点分别是A,B,易得,,由此建立a,c的齐次式,进而可得结果.
【详解】设椭圆与正三角形另两条边的交点分别是A,B,
易得,,
∴,∴,
∴,
故选:D.
4. 已知的一段图象如图所示,则( )
A.
B. 的图象的一个对称中心为
C. 的单调递增区间是
D. 函数的图象向左平移个单位后得到的是一个奇函数的图象
【答案】C
【解析】
【分析】首先根据函数图像求出函数解析式,即可判断A,再根据正弦函数的性质一一判断即可;
【详解】解:由图可知,,所以,解得,所以,又函数过点,即,所以,解得,因为,所以,所以,故A错误;
因为,所以函数关于对称,故B错误;
令,解得,故函数的单调递增区间为,故C正确;
将函数的图象向左平移个单位得为偶函数,故D错误;
故选:C
5. 用一个边长为4的正方形纸片,做一个如图所示的几何体,图中两个圆锥等底、等高,则该几何体体积的最大值为( )
A. B. C. D.
【答案】A
【解析】
【分析】通过圆锥侧面展开图的两种情况①侧面展开图最大为半径为2的半圆,②侧面展开图最大为半径为的四分之一圆,计算比较即可.
【详解】根据题意有两种方式可以得到这样的几何体,
方式一:如图①,可以得到圆锥的侧面展开图最大为半径为2的半圆,
因此一个圆锥的底面半径为1,母线长为2,高为,
所以两个圆锥体积的最大值为.
方式二:如图②,可以得到圆锥的侧面展开图最大为半径为的四分之一圆,
因此一个圆锥的底面半径为,母线长为,高为,
所以两个圆锥体积的最大值为.
,
故选:A.
6. 若,则的大小关系为( )
A. B. C. D.
【答案】D
【解析】
【分析】结合结论若,则,证明,由此可得,再证明,由此可得结论.
【详解】若,则,且,
所以,
所以,
因为,,
所以,
所以,
故选:D.
7. 元旦联欢会会场中挂着如图所示的两串灯笼, 每次随机选取其中一串并摘下其最下方的一个灯笺, 直至某一串灯笼被摘完为止, 则右侧灯笼先被摘完的概率为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据题意,得到摘取的次数为次,结合独立重复实验的概率计算公式,即可求解.
【详解】根据题意,直至某一串灯笼被摘完为止,可得摘取的次数为次,
结合独立重复实验的概率计算公式,可得:
当两次摘完时,可得概率为;
当三次摘完时,可得概率为;
当四次摘完时,可得概率为,则.
故选:D.
8. 如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或向上或右下移动,而一条移动路线由若干次移动构成,如从1移动到11:1→2→3→5→7→8→9→10→11就是一条移动路线.从1移动到数字的不同路线条数记为,从1移动到11的事件中,跳过数字的概率记为,则下列结论正确的是( )
①,②,③,④.
A. ①②③B. ①②④C. ②③④D. ①②③④
【答案】A
【解析】
【分析】根据题意分析,不难得到,按照规律写出各项,即可判断①,②正确;对于③,结合树状图,考虑对立事件所包含的样本点数,利用古典概型概率公式计算即得,同法求出即可判断.
【详解】由题意可知,
则,,
则①正确;显然,故②正确;
因为,经过数字5的路线共有条.
理由:如上树状图所示,分别计算1-5的路线共有5条,5-11的路线共有13条,
利用分步乘法计数原理可得,过数字5的路线共有条.
则,故③正确;
同理可得即有,故④错误.
故选:A.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知函数,则( )
A. 的图象关于直线对称
B. 的图象关于点对称
C. 区间上单调递减
D. 在区间的值域为
【答案】ABD
【解析】
【分析】根据正弦函数的性质逐一判断即可.
【详解】因,
选项A:,所以的图象关于直线对称,A说法正确;
选项B:,所以的图象关于点对称,B说法正确;
选项C:当时,,因为在单调递增,所以在区间上单调递增,C说法错误;
选项D:当时,,因为在的值域为,
所以在区间的值域为,D说法正确;
故选:ABD
10. 已知点为抛物线的焦点,为上不重合的两个动点,为坐标原点,若直线(直线斜率存在且不为0)与仅有唯一交点,则( )
A. 的准线方程为
B. 若线段与的交点恰好为中点,则
C. 直线与直线垂直
D. 若,则
【答案】ABC
【解析】
【分析】根据抛物线准线的定义即可判断A;求出线段的中点坐标,代入抛物线方程,即可判断B;设直线的方程为,联立方程,根据,结合直线的斜率公式即可判断C;根据焦半径公式即可判断D.
【详解】对于A,由抛物线抛物线,得的准线方程为,故A正确;
对于B,F1,0,则线段的中点坐标为,则,解得,故B正确;
对于C,设直线的方程为,
联立,消得,则,所以,
则,所以直线与直线垂直,故C正确;
对于D,设,则,所以,
所以,所以,故D错误.
故选:ABC.
11. 如图所示的曲线被称为双纽线,该种曲线在生活中应用非常广泛,其代数形式可表示为坐标中(为坐标原点)动点到点的距离满足:,则( )
A. OP的最大值是
B. 若是曲线上一点,且在第一象限,则
C. 与有1个交点
D. 面积的最大值是
【答案】ACD
【解析】
【分析】根据对称性可知运动到轴上时,此时OP最大,即可求解A,根据特殊位置法即可求解B,利用与的交点,即可结合,求解C,利用判别式可得,即可求解D.
【详解】由双纽线的对称性可知:当运动到轴上时,此时OP最大,不妨设此时在轴的正半轴上,设此时,
由,得,解得,故OP的最大值是,A正确,
设Px,y,则,令,则,解得,而此时,不满足,故B错误,
联立与,则,解得,
故直线与曲线只有一个交点,而,,由A易知双纽线中,
根据对称性,只需研究上与的交点情况,显然只有原点这1个交点,C正确,
对于D,由可得,
令,则,该方程有实数根,故,解得,故,
,故D正确,
故选:ACD
【点睛】关键点点睛:根据与的交点,结合,,可判断与的交点,由二次型方程的根,利用判别式可求解最大的纵坐标.
三、填空题(本题共3小题,每小题5分,共15分)
12. 设抛物线的焦点为,过点作直线交抛物线于,两点,若,,则___________.
【答案】##
【解析】
【分析】设Ax1,y1,Bx2,y2,根据抛物的定义表示出,,再根据三角形相似得到,即可求出.
【详解】设Ax1,y1,Bx2,y2,抛物线的焦点为,准线为,
因为,,根据抛物线的定义可得,,
过点作轴于点,过点作轴于点,
则,所以,
所以,即,解得.
故答案为:.
13. 若曲线在点处的切线与曲线相切,则________.
【答案】
【解析】
【分析】根据导数的几何意义求出切线方程,再联立切线方程与,消元,根据计算可得.
【详解】由,所以,则,
所以曲线在点处的切线为,即;
又与曲线相切,
由,可得,
则,解得或(舍去),
故答案为:
14. 某射击比赛中,甲、乙两名选手进行多轮射击对决.每轮射击中,甲命中目标的概率为,乙命中目标的概率为.若每轮射击中,命中目标的选手得1分,未命中目标的选手得0分,且各轮射击结果相互独立.则进行五轮射击后,甲的总得分不小于3的概率为__________.
【答案】
【解析】
【分析】利用相互独立事件、互斥事件的概率公式计算可得答案.
【详解】则进行五轮射击后,甲的总得分不小于3的概率为
.
故答案为:.
四、解答题: 本题共 5 小题. 解答应写出文字说明、证明过程或演算步骤.
15. 在中,a,b,c分别为角A,B,C的对边,已知,且.
(1)求角A的大小;
(2)求面积的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)先利用正弦定理边化角,然后利用两角和的余弦公式及诱导公式变形可得答案;
(2)先利用余弦定理及基本不等式求出的最大值,进而可得面积的最大值.
【小问1详解】
,
,
,,
,;
【小问2详解】
由余弦定理可得:,
即,
则,,当且仅当时,等号成立.
,
面积的最大值为.
16. 已知数列{an}的前n项和为Sn,a1=2,an+1=2Sn+2.
(1)求数列{an}的通项公式;
(2)若2bn=3nan,求数列{bn}的前n项和Tn.
【答案】(1)
(2)
【解析】
【分析】(1)由的关系可得,求出,再由的关系,得到,进而根据等比定义求得{an}的通项公式;
(2),由错位相减法可求得{bn}的前n项和Tn.
小问1详解】
,
为首项是3,公比为3的等比数列,,
当时,,
当时,,符合上式,
【小问2详解】
,
,
,
.
17. 在中,角的对边分别为的面积为,已知.
(1)求角;
(2)若的周长为,求的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)利用正弦定理及三角恒等变换即可求解;
(2)由余弦定理及三角形的面积公式得,再由基本不等式进行求解即可.
【小问1详解】
因为,
所以,
即,
由正弦定理,得,
因为,
所以,
因为,所以,所以,
又,所以.
【小问2详解】
由余弦定理,得,即,
所以,即,
因为,,
所以,
所以,
又(当且仅当时取等号),
所以(当且仅当时取等号),
所以(当且仅当时取等号),
所以(当且仅当时取等号),
即的最大值为.
18. 正四棱柱中,点分别在上,且四点共面.
(1)若,记平面与底面的交线为,证明:;
(2)已知,若,求四边形面积的最大值.
【答案】(1)证明见解析
(2)2
【解析】
【分析】(1)连接,利用已知可得四边形是平行四边形,进而可得平面,由线面平行的性质可得;
(2)以为坐标原点,为坐标轴建立如图所示的空间直角坐标系,由已知可得四边形是平行四边形,进而可得,结合已知计算可求四边形面积的最大值.
【小问1详解】
连接,
由正四棱柱,可得,,,又因为,所以由勾股定理可得,
又,所以,所以四边形是平行四边形,
所以,又平面,平面,
所以平面,又平面平面,平面平面,
所以,所以;
【小问2详解】
以为坐标原点,为坐标轴建立如图所示的空间直角坐标系,
因为,又底面是正方形,所以,
又,所以,
所以,
所以,
所以,
,
由正四棱柱,可得平在面,
又四点共面,过有唯一平面,
又平面平面,平面平面,
所以,同理可得,所以四边形是平行四边形,
又,所以,
所以,又,
所以,解得,
所以
,
所以四边形面积的最大值为.
19. 在高中数学教材苏教版选择性必修2上阐述了这样一个问题:假设某种细胞分裂(每次分裂都是一个细胞分裂成两个)和死亡的概率相同,如果一个种群从这样的一个细胞开始变化,那么这个种群最终灭绝的概率是多少?在解决这个问题时,我们可以设一个种群由一个细胞开始,最终灭绝的概率为,则从一个细胞开始,它有的概率分裂成两个细胞,在这两个细胞中,每个细胞灭绝的概率都是,两个细胞最终都走向灭绝的概率就是,于是我们得到:,计算可得;我们也可以设一个种群由一个细胞开始,最终繁衍下去的概率为,那么从一个细胞开始,它有的概率分裂成两个细胞,在这两个细胞中,每个细胞繁衍下去的概率都是,两个细胞最终都走向灭绝的概率就是,于是我们得到:,计算可得.根据以上材料,思考下述问题:一个人站在平面直角坐标系的点处,他每步走动都会有的概率向左移动1个单位,有的概率向右移动一个单位,原点处有一个陷阱,若掉入陷阱就会停止走动,以代表当这个人由开始,最终掉入陷阱的概率.
(1)若这个人开始时位于点处,且.
(ⅰ)求他在5步内(包括5步)掉入陷阱的概率;
(ⅱ)求他最终掉入陷阱的概率;
(ⅲ)已知,若,求;
(2)已知是关于的连续函数.
(ⅰ)分别写出当和时,的值(直接写出即可,不必说明理由);
(ⅱ)求关于表达式.
【答案】(1)(ⅰ);(ⅱ);(ⅲ)
(2)(ⅰ)当时,;当时,;(ⅱ)
【解析】
【分析】(1)应用全概率公式分互斥事件计算概率,再根据递推公式构造数列,计算得出等比数列结合累加法得出通项公式;
(2)针对定义域分段求解函数表达式.
【小问1详解】
(ⅰ)设事件:“这个人在第1步掉入陷阱”,事件:“这个人在第3步掉入陷阱”,事件:“这个人在第5步掉入陷阱”,
则他在5步内掉入陷阱的概率.
(ⅱ)他从1,0开始,最终掉入陷阱的概率为,则这个人如果第一步向左走,就会掉入陷阱,
若他第一步向右走,如果最终掉入陷阱,则需要由2,0先到达1,0处,
而这个概率和他从1,0开始,最终掉入陷阱的概率相同,所以,
由此可得(舍去)或.
(ⅲ)由(ⅱ)可知,,
方法一:由,得,
所以是以为首项,为公比的等比数列,
则.
则
累加得,所以.
方法二:由,得,即,
所以是以为首项,为公比等比数列,所以.
【小问2详解】
(ⅰ)由题意得,当时,;当时,.
(ⅱ)这个人如果第一步向左走,就会掉入陷阱,
若他第一步向右走,如果最终掉入陷阱,则需要由2,0先到达1,0处,
而这个概率和他从1,0开始,最终掉入陷阱的概率相同,
所以,即,得或.
因为是关于的连续函数,所以当时,,
当时,.
所以
【点睛】关键点点睛:根据递推公式构造数列,计算得出等比数列,结合累加法得出通项公式.
相关试卷
这是一份吉林省通化市梅河口市第五中学2024-2025学年高三上学期9月月考数学试题,文件包含吉林省通化市梅河口市第五中学2025届高三上学期9月月考数学试题原卷版docx、吉林省通化市梅河口市第五中学2025届高三上学期9月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
这是一份吉林省通化市梅河口市第五中学2025届高三上学期9月月考数学试题(解析版)_create,共20页。
这是一份数学丨吉林省通化市梅河口市第五中学2025年新高三6月月考数学试卷及答案,共19页。








