2024-2025学年河北省石家庄部分学校九上数学开学教学质量检测试题【含答案】

这是一份2024-2025学年河北省石家庄部分学校九上数学开学教学质量检测试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，在四边形中，下列条件不能判定四边形是平行四边形的是（ ）
A．B．
C．D．
2、（4分）如图，在平行四边形ABCD中，AB=4，CE平分∠BCD交AD边于点E，且AE=3，则BC的长为（ ）
A．4B．6C．7D．8
3、（4分）把分式中、的值都扩大为原来的2倍，分式的值（ ）
A．缩小为原来的一半B．扩大为原来的2倍
C．扩大为原来的4倍D．不变
4、（4分）一次函数分别交轴、轴于，两点，在轴上取一点，使为等腰三角形，则这样的点最多有几个（ ）
A．5B．4C．3D．2
5、（4分）化简的结果是
A．+1B．C．D．
6、（4分）下列不能反映一组数据集中趋势的是（ ）
A．众数B．中位数C．方差D．平均数
7、（4分）如图，在菱形ABCD中，AB=4，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（ ）
A．2B．2C．4D．2+2
8、（4分）如图所示，在平行四边形中，对角线和相交于点，交于点，若，则的长为（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则GT的长为_____．
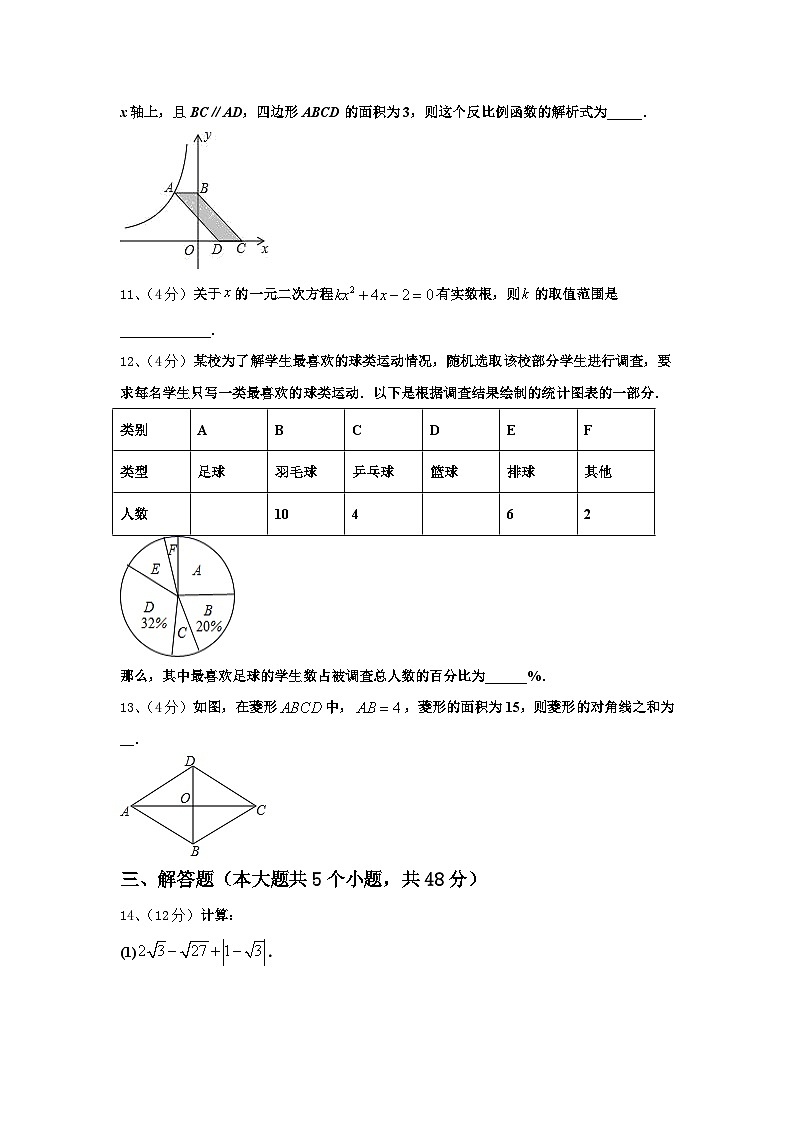
10、（4分）如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点C、D在x轴上，且BC∥AD，四边形ABCD的面积为3，则这个反比例函数的解析式为_____．
11、（4分）关于的一元二次方程有实数根，则的取值范围是_____________.
12、（4分）某校为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动．以下是根据调查结果绘制的统计图表的一部分．
那么，其中最喜欢足球的学生数占被调查总人数的百分比为______%．
13、（4分）如图，在菱形中，，菱形的面积为15，则菱形的对角线之和为__．
三、解答题（本大题共5个小题，共48分）
14、（12分）计算：
(1).
(2).
(3).
(4)解方程：.
15、（8分）小黄人在与同伴们研究日历时发现了一个有趣的规律：
若用字母n表示平行四边形中左上角位置的数字，请你用含n的式子写出小黄人发现的规律，并加以证明.
16、（8分）先化简，再求值：，其中x＝1．
17、（10分）在矩形中，点在上，，，垂足为．
（1）求证：；
（2）若，且，求．
18、（10分）如图，在中，，分别是边，上的点，且．求证：四边形为平行四边形．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）对于代数式m，n，定义运算“※”：m※n＝（mn≠0），例如：4※2＝．若（x﹣1）※（x+2）＝，则2A﹣B＝_____．
20、（4分）已知数据a1，a2，a3，a4，a5的平均数是m，且a1＞a2＞a3＞a4＞a5＞0，则数据a1，a2，a3，﹣3，a4，a5的平均数和中位数分别是_____，_____．
21、（4分）如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图，则喜爱“体育”节目的人数是_____人．
22、（4分）如图，小巷左右两侧是竖直的墙．一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7m，顶端距离地面2.4m．若梯子底端位置保持不动，将梯子斜靠在右墙时，顶端距离地面2m，则小巷的宽度为_____m．
23、（4分）如图，Rt△ABC中，∠BAC=90°，AB=6，AC=8,P为BC上一动点，PE⊥AB于E，PF⊥AC于F,则EF最小值是________.
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，菱形ABCD的边长为20cm，∠ABC＝120°．动点P、Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q以2cm/s的速度，沿A→C的路线向点C运动．当P、Q到达终点C时，整个运动随之结束，设运动时间为t秒．
（1）在点P、Q运动过程中，请判断PQ与对角线AC的位置关系，并说明理由；
（2）若点Q关于菱形ABCD的对角线交点O的对称点为M，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N．
①当t为何值时，点P、M、N在一直线上？
②当点P、M、N不在一直线上时，是否存在这样的t，使得△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．
25、（10分）为响应绿色出行号召，越来越多市民选择租用共享单车出行，已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式，如图描述了两种方式应支付金额y（元）与骑行时间x（时）之间的函数关系，根据图象回答下列问题：
（1）求手机支付金额y（元）与骑行时间x（时）的函数关系式；
（2）李老师经常骑行共享单车，请根据不同的骑行时间帮他确定选择哪种支付方式比较合算．
26、（12分）如图，在平面直角坐标系中，直线与轴，轴的交点分别为，直线交轴于点，两条直线的交点为，点是线段上的一个动点，过点作轴，交轴于点，连接.
求的面积；
在线段上是否存在一点，使四边形为矩形，若存在，求出点坐标：若不存在，请说明理由；
若四边形的面积为，设点的坐标为，求出关于的函数关系式，并写出自变量的取值范围.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据平行四边形的5种判定方法分别进行分析即可．
【详解】
A. 根据两组对边分别平行，是平行四边形可判定四边形ABCD是平行四边形，故此选项不合题意；
B. 根据两组对边分别相等，是平行四边形可判定四边形ABCD是平行四边形，故此选项不合题意；
C.不能判定判定四边形ABCD是平行四边形，故此选项符合题意；
D. 根据一组对边平行且相等，是平行四边形可判定四边形ABCD是平行四边形，故此选项不合题意；
故选C.
此题考查平行四边形的判定，解题关键在于掌握判定定理
2、C
【解析】
由平行四边形的性质可得AD∥BC，且AD=BC，结合角平分线的性质可求得DE=DC=AB=1，则可求得AD的长，可求得答案．
【详解】
解：∵四边形ABCD为平行四边形，∴AB=CD=1，AD∥BC，AD=BC，∴∠DEC=∠BCE．∵CE平分∠BCD，∴∠DCE=∠BCE，∴∠DEC=∠DCE，∴DE=DC=1．
∵AE=3，∴AD=BC=3+1=2．
故选C．
本题主要考查平行四边形的性质，利用平行线的性质及角平分线的性质求得DE=DC是解题的关键．
3、D
【解析】
根据分式的分子分母都乘以或除以同一个不为零的数或者整式,分式的值不变,可得答案.
【详解】
把分式中的x和y的值都扩大到原来的2倍,得
故选D.
本题考查了分式的基本性质,分式的分子分母都乘以或除以同一个不为零的数或者整式,分式的值不变.
4、B
【解析】
首先根据题意，求得与的坐标，然后利用勾股定理求得的长，再分别从，，去分析求解，即可求得答案．
【详解】
解：当时，，当时，，
，，
，
①当时，，
；
②当时，，，
③当时，设的坐标是，，，
，由勾股定理得：，
解得：，
的坐标是，，
这样的点最多有4个．
故选：B．
此题考查了等腰三角形的性质、一次函数的性质以及勾股定理．此题难度适中，注意掌握数形结合思想与分类讨论思想的应用．
5、D
【解析】
试题分析：．故选D．
6、C
【解析】
试题分析：平均数、众数、中位数是描述一组数据集中趋势的特征量，极差、方差是衡量一组数据偏离其平均数的大小（即波动大小）的特征数．故答案选C．
考点：统计量的选择.
7、B
【解析】
解：作点P关于BD的对称点P′，作P′Q⊥CD交BD于K，交CD于Q，
∵AB=4，∠A=120°，
∴点P′到CD的距离为4×=，
∴PK+QK的最小值为，
故选B．
本题考查轴对称-最短路线问题；菱形的性质．
8、B
【解析】
由平行四边形ABCD中，对角线AC和BD交于点O，OE∥BC，可得OE是△ACD的中位线，根据三角形中位线的性质，即可求得AD的长．
【详解】
解：∵四边形ABCD是平行四边形，
∴OA=OC，AD∥BC，
∵OE∥BC，
∴OE∥AD，
∴OE是△ACD的中位线，
∵OE=4cm，
∴AD=2OE=2×4=8（cm）．
故选：B．
此题考查了平行四边形的性质以及三角形中位线的性质．此题比较简单，注意掌握数形结合思想的应用．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、2
【解析】
根据正方形的对角线平分一组对角可得∠ADB=∠CGE=45°，再求出∠GDT=45°，从而得到△DGT是等腰直角三角形，根据正方形的边长求出DG，再根据等腰直角三角形的直角边等于斜边的倍求解即可．
【详解】
∵BD、GE分别是正方形ABCD，正方形CEFG的对角线，
∴∠ADB=∠CGE=45°，
∴∠GDT=180°−90°−45°=45°，
∴∠DTG=180°−∠GDT−∠CGE=180°−45°−45°=90°，
∴△DGT是等腰直角三角形，
∵两正方形的边长分别为4，8，
∴DG=8−4=4，
∴GT=×4=2.
故答案为2.
本题考查了正方形的性质，等腰直角三角形的判定与性质．关键是掌握正方形的对角线平分一组对角
10、
【解析】
解：过A点向x轴作垂线，如图：
根据反比例函数的几何意义可得：四边形ABCD的面积为3，即|k|=3，
又∵函数图象在二、四象限，
∴k=﹣3，
即函数解析式为：y=﹣．
故答案为y=﹣．
本题考查反比例函数系数k的几何意义．
11、且
【解析】
根据∆≥0，且k≠0列式求解即可.
【详解】
由题意得
∆=16+8k≥0且k≠0,
解之得
且.
故答案为：且.
本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式∆=b2﹣4ac与根的关系，熟练掌握根的判别式与根的关系式解答本题的关键.当∆>0时，一元二次方程有两个不相等的实数根；当∆=0时，一元二次方程有两个相等的实数根；当∆