2024-2025学年河南省汝州数学九上开学经典模拟试题【含答案】

这是一份2024-2025学年河南省汝州数学九上开学经典模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知m＝ ，则（ ）
A．4＜m＜5B． 6＜m＜7C．5＜m＜6D．7＜m＜8
2、（4分）向一容器内均匀注水,最后把容器注满在注水过程中,容器的水面高度与时间的关系如图所示,图中PQ为一线段,则这个容器是( )
A．B．C．D．
3、（4分）若正比例函数y=kx的图象经过点（1，2），则k的值为
A．B．－2C．D．2
4、（4分）某校举行课间操比赛，甲、乙两个班各选出20名学生参加比赛，两个班参赛学生的平均身高都为1.65m，其方差分别是S甲2＝3.8，S乙2＝3.4，则参赛学生身高比较整齐的班级是（ ）
A．甲班B．乙班C．同样整齐D．无法确定
5、（4分）如图，在数轴上，点A表示的数是2，△OAB是Rt△，∠OAB＝90°，AB＝1，现以点O为圆心，线段OB长为半径画弧，交数轴负半轴于点C，则点C表示的实数是( )
A．﹣B．﹣C．﹣3D．﹣2
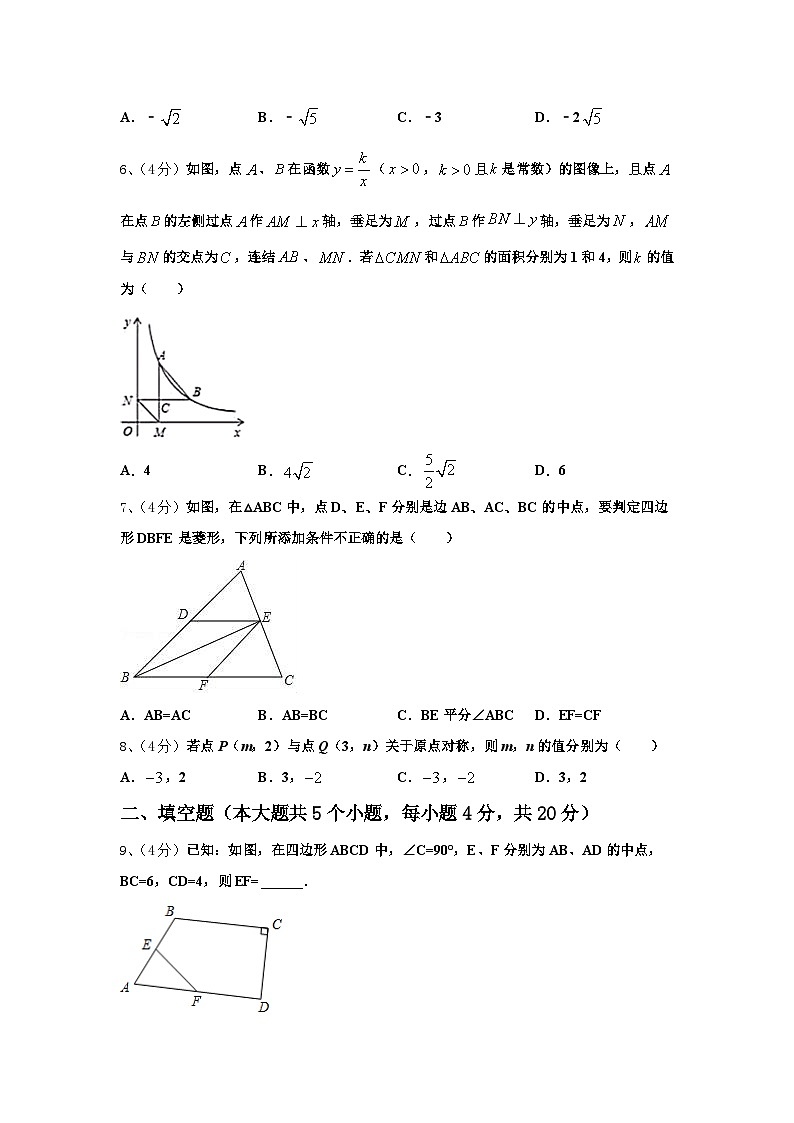
6、（4分）如图，点、在函数（，且是常数）的图像上，且点在点的左侧过点作轴，垂足为，过点作轴，垂足为，与的交点为，连结、．若和的面积分别为1和4，则的值为（ ）
A．4B．C．D．6
7、（4分）如图，在△ABC中，点D、E、F分别是边AB、AC、BC的中点，要判定四边形DBFE是菱形，下列所添加条件不正确的是（ ）
A．AB=ACB．AB=BCC．BE平分∠ABCD．EF=CF
8、（4分）若点P（m，2）与点Q（3，n）关于原点对称，则m，n的值分别为（ ）
A．，2B．3，C．，D．3，2
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知：如图，在四边形ABCD中，∠C=90°，E、F分别为AB、AD的中点，BC=6，CD=4，则EF=______．
10、（4分）八年级（3）班共有学生50人，如图是该班一次信息技术模拟测试成绩的频数分布直方图（满分为50分，成绩均为整数），若不低于30分为合格，则该班此次成绩达到合格的同学占全班人数的百分比是__________．
11、（4分）如图，▱ABCD的对角线AC、BD相交于点O，点E是CD的中点；若AD=8cm，则OE的长为_______．
12、（4分）阅读下面材料：
在数学课上，老师提出如下问题：
尺规作图：作一条线段的垂直平分线．
已知：线段AB．
求作：线段AB的垂直平分线．
小红的作法如下：
如图，①分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于点C；
②再分别以点A和点B为圆心，大于AB的长为半径（不同于①中的半径）作弧，两弧相交于点D，使点D与点C在直线AB的同侧；
③作直线CD．
所以直线CD就是所求作的垂直平分线．
老师说：“小红的作法正确．”
请回答：小红的作图依据是_____．
13、（4分）已知点P（1，2）关于x轴的对称点为P′，且P′在直线y=kx+3上，把直线y=kx+3的图象向上平移2个单位，所得的直线解析式为 ．
三、解答题（本大题共5个小题，共48分）
14、（12分）为贯彻党的“绿水青山就是金山银山”的理念，我市计划购买甲、乙两种树苗共7000株用于城市绿化，甲种树苗每株24元，一种树苗每株30元相关资料表明：甲、乙两种树苗的成活率分别为、．
若购买这两种树苗共用去180000元，则甲、乙两种树苗各购买多少株？
若要使这批树苗的总成活率不低于，则甲种树苗至多购买多少株？
在的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．
15、（8分）目前由重庆市教育委员会，渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕，重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖，重庆一中获优秀组织奖，重庆一中老师李珊获先进个人奖，其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛，若以下两个统计图统计了舞蹈组各代表队的得分情况：
（1）m＝ ，在扇形统计图中分数为7的圆心角度数为 度．
（2）补全条形统计图，各组得分的中位数是 分，众数是 分．
（3）若舞蹈组获得一等奖的队伍有2组，已知主办方各组的奖项个数是按相同比例设置的，若参加该展演活动的总队伍数共有120组，那么该展演活动共产生了多少个一等奖？
16、（8分）同学们，我们以前学过完全平方公式，你一定熟悉掌握了吧！现在，我们又学习了二次根式，那么所有非负数都可以看作是一个数的平方，如，，下面我们观察：
；
反之，；
∴；
∴.
仿上例，求：
（1）；
（2）若，则、与、的关系是什么？并说明理由.
17、（10分）已知边长为1的正方形ABCD中,P是对角线AC上的一个动点(与点A．C不重合)，过点P作PE⊥PB，PE交射线DC于点E，过点E作EF⊥AC，垂足为点F，当点E落在线段CD上时(如图)，
（1）求证：PB=PE；
（2）在点P的运动过程中，PF的长度是否发生变化?若不变，试求出这个不变的值，若变化，试说明理由；
18、（10分）如图所示的图象反映的过程是：小强星期天从家跑步去体育场，在那里锻炼了一会儿后又走到文具店去买笔，然后步行回家，其中x表示时间，y表示小强离家的距离，根据图象回答下列问题．
(1)体育场离小强家有多远？小强从家到体育场用了多长时间？
(2)体育场距文具店多远？
(3)小强在文具店逗留了多长时间？
(4)小强从文具店回家的平均速度是多少？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，矩形OABC中，D为对角线AC，OB的交点，直线AC的解析式为，点P是y轴上一动点，当的周长最小时，线段OP的长为______．
20、（4分）如图，在轴的正半轴上，自点开始依次间隔相等的距离取点，，，，，，分别过这些点作轴的垂线，与反比例函数的图象交于点，，，，，，作，，，，，垂足分别为，，，，，，连结，，，，，得到一组，，，，，它们的面积分别记为，，，，，则_________，_________．
21、（4分）若正多边形的一个内角等于150°，则这个正多边形的边数是______．
22、（4分）如图，在直角坐标平面内的△ABC中，点A的坐标为（0，2），点C的坐标为（5，5），如果要使△ABD与△ABC全等，且点D坐标在第四象限，那么点D的坐标是__________；
23、（4分）若方程（k为常数）有两个不相等的实数根，则k取值范围为 ．
二、解答题（本大题共3个小题，共30分）
24、（8分）在平行四边形中，的垂直平分线分别交于两点，交于点，试判断四边形的形状，并说明理由.
25、（10分）如图，已知，在平面直角坐标系中，A（﹣3，﹣4），B（0，﹣2）．
（1）△OAB绕O点旋转180°得到△OA1B1，请画出△OA1B1，并写出A1，B1的坐标．
（2）判断以A，B，A1，B1为顶点的四边形的形状，请直接在答卷上填写答案．
26、（12分）解方程：x2-3x=5x-1
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据被开方数越大算术平方根越大，可得答案．
【详解】
∵ ＜＜ ，
∴5＜m＜6，
故选：C．
本题考查了估算无理数的大小，解题关键在于掌握运算法则.
2、C
【解析】
观察图象，开始上升缓慢，最后匀速上升，再针对每个容器的特点，选择合适的答案解答即可．
【详解】
根据图象，水面高度增加的先逐渐变快，再匀速增加；
故容器从下到上，应逐渐变小，最后均匀.
故选C.
此题考查函数的图象，解题关键在于结合实际运用函数的图像.
3、D
【解析】
∵正比例函数y=kx的图象经过点（1，1），
∴把点（1，1）代入已知函数解析式，得k=1．故选D．
4、B
【解析】
根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定
【详解】
S甲2＝3.8，S乙2＝3.4，
∴S甲2＞S乙2，
∴参赛学生身高比较整齐的班级是乙班，
故选：B．
此题主要考查了方差，方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
5、B
【解析】
直接根据勾股定理，在Rt△AOB中，，求出OB长度，再求出OC长度，结合数轴即可得出结论．
【详解】
解：∵在Rt△AOB中，OA=2，AB=1，
∴OB==．
∵以O为圆心，以OB为半径画弧，交数轴的正半轴于点C，
∴OC=OB=，
∴点C表示的实数是-．
故选B．
本题考查的是实数与数轴以及复杂作图，熟知实数与数轴上各点是一一对应关系是解答此题的关键．
6、D
【解析】
设点M（a，0），N（0，b），然后可表示出点A、B、C的坐标，根据的面积为1可求出ab＝2，根据的面积为4列方程整理，可求出k．
【详解】
解：设点M（a，0），N（0，b），
∵AM⊥x轴，且点A在反比例函数的图象上，
∴点A的坐标为（a，），
∵BN⊥y轴，
同理可得：B（，b），则点C（a，b），
∵S△CMN＝NC•MC＝ab＝1，
∴ab＝2，
∵AC＝−b，BC＝−a，
∴S△ABC＝AC•BC＝(−b)•(−a)＝4，即，
∴，
解得：k＝6或k＝−2（舍去），
故选：D．
本题考查反比例函数图象上点的坐标特征、三角形的面积计算等，解答本题的关键是明确题意，利用三角形的面积列方程求解．
7、A
【解析】
当AB=BC时，四边形DBFE是菱形．根据三角形中位线定理证明即可；当BE平分∠ABC时，可证BD=DE，可得四边形DBFE是菱形，当EF=FC，可证EF=BF，可得四边形DBFE是菱形，由此即可判断；
【详解】
解：当AB=BC时，四边形DBFE是菱形；
理由：∵点D、E、F分别是边AB、AC、BC的中点，
∴DE∥BC，EF∥AB，
∴四边形DBFE是平行四边形，
∵DE=BC，EF=AB，
∴DE=EF，
∴四边形DBFE是菱形．
故B正确，不符合题意，
当BE平分∠ABC时，∴∠ABE=∠EBC
∵DE∥BC，
∴∠CBE=∠DEB
∴∠ABE =∠DEB
∴BD=DE
∴四边形DBFE是菱形，
故C正确，不符合题意，
当EF=FC，
∵BF=FC
∴EF=BF，
∴四边形DBFE是菱形，
故D正确，不符合题意，
故选A．
本题考查三角形的中位线定理，平行四边形的判定和性质，菱形的判定等知识，解题的关键是熟练掌握三角形中位线定理，属于中考常考题型．
8、C
【解析】
根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．
【详解】
点P（m，2）与点Q（3，n）关于原点对称，得
m=-3，n=-2，
故选：C．
本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
连接BD，利用勾股定理列式求出BD，再根据三角形的中位线平行于第三边并且等于第三边的一半解答．
【详解】
解：如图，连接BD，
∵∠C=90°，BC=6，CD=4，
∴BD===2，
∵E、F分别为AB、AD的中点，
∴EF是△ABD的中位线，
∴EF=BD=×2=．
故答案为：．
本题考查了三角形的中位线平行于第三边并且等于第三边的一半，勾股定理，熟记定理是解题的关键，难点在于作辅助线构造出三角形．
10、70%
【解析】
利用合格的人数即50-10-5=35人，除以总人数即可求得．
【详解】
解：该班此次成绩达到合格的同学占全班人数的百分比是×100%=70%．
故答案是：70%．
本题考查了读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
11、4cm
【解析】
先说明OE是△ACD的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半求解．
【详解】
∵▱ABCD的对角线AC、BD相交于点O，
∴OA=OC，
∵点E是CD的中点，
∴CE=DE，
∴OE是△ACD的中位线，
∵AD=8cm，
∴OE=AD=×8=4cm，
故答案为：4cm．
本题考查了平行四边形的性质，三角形中位线定理，熟练掌握相关的性质定理是解题的关键.
12、到线段两个端点距离相等的点在这条线段的垂直平分线上；两点确定一条直线．
【解析】
分析：根据线段垂直平分线的作法即可得出结论．
详解：如图，
∵由作图可知，AC=BC=AD=BD，
∴直线CD就是线段AB的垂直平分线．
故答案为：到线段两个端点距离相等的点在这条线段的垂直平分线上；两点确定一条直线．
点睛：本题考查的是作图-基本作图，熟知线段垂直平分线的作法是解答此题的关键．
13、y=﹣1x+1．
【解析】
由对称得到P′（1，﹣2），再代入解析式得到k的值，再根据平移得到新解析式.
【详解】
∵点P（1，2）关于x轴的对称点为P′，
∴P′（1，﹣2），
∵P′在直线y=kx+3上，
∴﹣2=k+3，解得：k=﹣1，
则y=﹣1x+3，
∴把直线y=kx+3的图象向上平移2个单位，所得的直线解析式为：y=﹣1x+1．
故答案为y=﹣1x+1．
考点：一次函数图象与几何变换．
三、解答题（本大题共5个小题，共48分）
14、甲、乙两种树苗各购买5000、2000株；甲种树苗至多购买2800株；最少费用为 元.
【解析】
列方程求解即可；
根据题意，甲乙两种树苗的存货量大于等于树苗总量的列出不等式；
用x表示购买树苗的总费用，根据一次函数增减性讨论最小值．
【详解】
设购买甲种树苗x株，则购买乙种树苗株，
由题意得：
解得，则
答：甲、乙两种树苗各购买5000、2000株；
根据题意得：
解得
则甲种树苗至多购买2800株
设购买树苗的费用为W，
根据题意得：
随x的增大而减小
当时，
本题为一次函数实际应用问题，综合考察一元一次方程、一元一次不等式及一次函数的增减性．
15、（1）25，54；（2）如图所示见解析；6.5，6；（3）该展演活动共产生了12个一等奖．
【解析】
（1）根据条形统计图和扇形统计图中的数据，即可得到总的组数，进而得出各分数对应的组数以及圆心角度数；（2）根据中位数以及众数的定义进行判断，即可得到中位数以及众数的值；（3）依据舞蹈组获得一等奖的队伍的比例，即可估计该展演活动共产生一等奖的组数．
【详解】
（1）10÷50%＝20（组），20﹣2﹣3﹣10＝5（组），
m%＝×100%＝25%，
×360°＝54°，
故答案为：25，54；
（2）8分这一组的组数为5，如图所示：
各组得分的中位数是（7+6）＝6.5，
分数为6分的组数最多，故众数为6；
故答案为：6.5，6；
（3）由题可得，×120＝12（组），
∴该展演活动共产生了12个一等奖．
本题主要考查了条形统计图以及扇形统计图的应用，通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系，从条形图可以很容易看出数据的大小，便于比较．
16、（1）；（2），.理由见解析.
【解析】
（1）根据阅读材料即可求解；
（2）根据阅读材料两边同时平方即可求解.
【详解】
（1）
；
（2），；
∵，∴，
∴，
∴，.
此题主要考查二次根式的性质，解题的关键是熟知二次根式的运算法则.
17、（1）见解析；（2）
【解析】
（1）过点P作PG⊥BC于G，过点P作PH⊥DC于H，如图1．要证PB=PE，只需证到△PGB≌△PHE即可；（2）连接BD，如图2．易证△BOP≌△PFE，则有BO=PF，只需求出BO的长即可．
【详解】
(1)①证明：过点P作PG⊥BC于G，过点P作PH⊥DC于H，如图1.
∵四边形ABCD是正方形，PG⊥BC，PH⊥DC，
∴∠GPC=∠ACB=∠ACD=∠HPC=45°.
∴PG=PH,∠GPH=∠PGB=∠PHE=90°.
∵PE⊥PB即∠BPE=90°，
∴∠BPG=90°−∠GPE=∠EPH.
在△PGB和△PHE中，
.
∴△PGB≌△PHE(ASA)，
∴PB=PE.
②连接BD，如图2.
∵四边形ABCD是正方形,∴∠BOP=90°.
∵PE⊥PB即∠BPE=90°，
∴∠PBO=90∘−∠BPO=∠EPF.
∵EF⊥PC即∠PFE=90°，
∴∠BOP=∠PFE.
在△BOP和△PFE中，
，
∴△BOP≌△PFE(AAS)，
∴BO=PF.
∵四边形ABCD是正方形，
∴OB=OC,∠BOC=90∘，
∴BC= OB.
∵BC=1,∴OB= ，
∴PF=.
∴点PP在运动过程中,PF的长度不变,值为.
此题考查正方形的性质，全等三角形的判定与性质，四边形综合题，解题关键在于作辅助线
18、（1）体育场离陈欢家2.5千米，小刚在体育场锻炼了15分钟；（2）体育场离文具店1千米；（3） 小刚在文具店停留20分；（4）小强从文具店回家的平均速度是千米/分
【解析】
（1）根据观察函数图象的纵坐标，可得距离，观察函数图象的横坐标，可得时间；
（2）根据观察函数图象的横坐标，可得体育场与文具店的距离；
（3）观察函数图象的横坐标，可得在文具店停留的时间；
（4）用回家的路程除以回家的时间即可.
【详解】
（1）由纵坐标看出体育场离陈欢家2.5千米，由横坐标看出小刚在体育场锻炼了15分钟；
（2）由纵坐标看出体育场离文具店3.5-2.5=1（千米）；
（3）由横坐标看出 小刚在文具店停留55-35=20（分）；
（4）小强从文具店回家的平均速度是3.5÷（125-55）=（千米/分）
本题考查了函数图象，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．需注意计算单位的统一．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据题意可以得到点A、B、C的坐标和点D的坐标，然后最短路径问题可以求得点P的坐标，从而可以求得OP的长．
【详解】
解：作点D关于y轴的对称点，连接交y轴于点P，则点P即为所求，
直线AC的解析式为，
当时，，当时，，
点A的坐标为，点C的坐标为，
点D的坐标为，点B的坐标为，
点的坐标为，
设过点B和点的直线解析式为，
，
解得，，
过点B和点的直线解析式为，
当时，，
即点P的坐标为，
.
故答案为．
本题考查一次函数的性质、矩形的性质、最短路线问题，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
20、
【解析】
设，根据反比例函数图象上点的坐标特征和三角形面积公式得到，，，依次可得,然后代入计算即可．
【详解】
解：设，
则，，，，
，，，
，
．
故答案为：，．
本题考查了反比例函数图像上点的坐标特征和三角形面积公式，求出三角形的面积并找到规律是解答本题的关键．
21、1．
【解析】
首先根据求出外角度数，再利用外角和定理求出边数．
【详解】
正多边形的一个内角等于，
它的外角是：，
它的边数是：．
故答案为：1．
此题主要考查了多边形的外角与内角，做此类题目，首先求出正多边形的外角度数，再利用外角和定理求出求边数．
22、（3，-3）
【解析】
根据全等三角形的性质，三条对应边均相等，又顶点C与顶点D相对应，所以点D与C关于AB对称，即点D与点C对与AB的相对位置一样．
【详解】
解：∵△ABD与△ABC全等，
∴C、D关于AB对称，顶点C与顶点D相对应，即C点和D点到AB的相对位置一样．
∵由图可知，AB平行于x轴，
∴D点的横坐标与C的横坐标一样，即D点的横坐标为3．
又∵点A的坐标为（0，2），点C的坐标为（3，3），点D在第四象限，
∴C点到AB的距离为2．
∵C、D关于AB轴对称，
∴D点到AB的距离也为2，
∴D的纵坐标为-3．
故D（3，-3）．
23、
【解析】
根据方程的系数结合根的判别式即可得出关于k的一元一次不等式，解不等式即可得出结论，
【详解】
解：∵方程（k为常数）的两个不相等的实数根，
∴>0，且，
解得：k