2024-2025学年湖北省天门天宜国际学校数学九上开学联考模拟试题【含答案】

这是一份2024-2025学年湖北省天门天宜国际学校数学九上开学联考模拟试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）某电信公司有A、B两种计费方案：月通话费用y（元）与通话时间x（分钟）的关系，如图所示，下列说法中正确的是（ ）
A．月通话时间低于200分钟选B方案划算
B．月通话时间超过300分钟且少于400分钟选A方案划算
C．月通话费用为70元时，A方案比B方案的通话时间长
D．月通话时间在400分钟内，B方案通话费用始终是50元
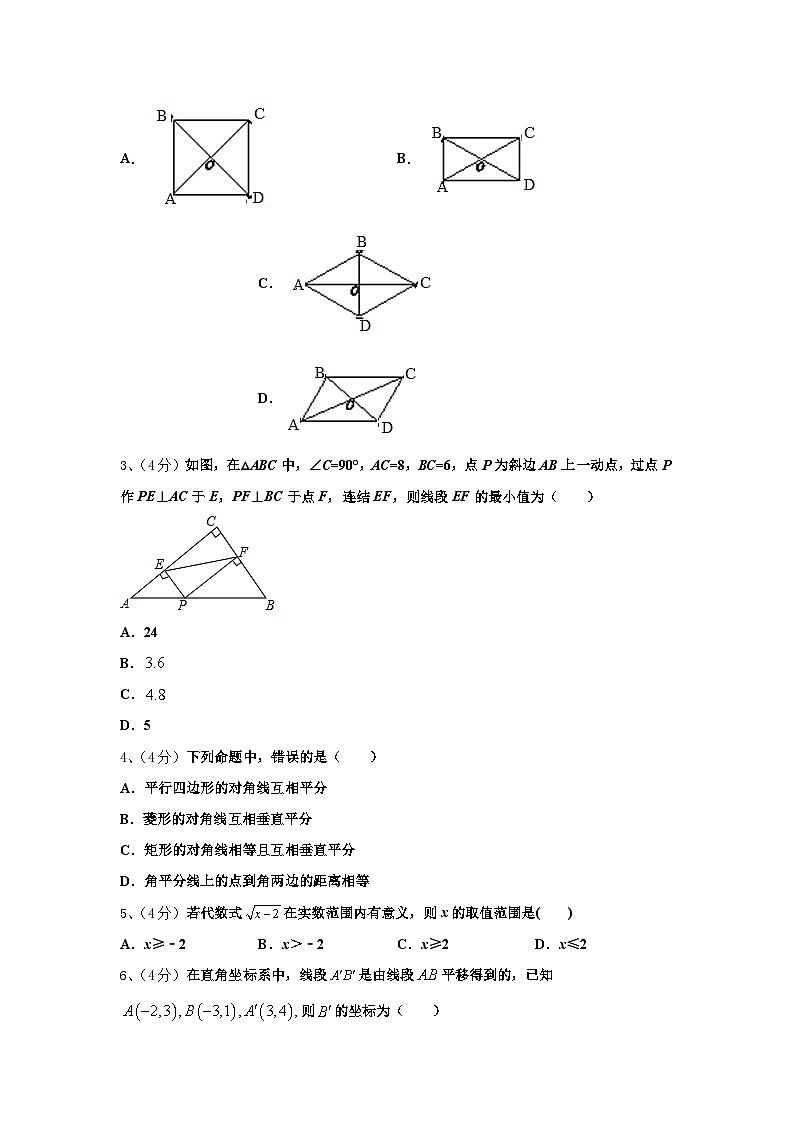
2、（4分）已知某四边形的两条对角线相交于点O．动点P从点A出发，沿四边形的边按A→B→C的路径匀速运动到点C．设点P运动的时间为x，线段OP的长为y，表示y与x的函数关系的图象大致如图所示，则该四边形可能是（ ）
A．B．C．D．
3、（4分）如图，在△ABC中，∠C=90°，AC=8，BC=6，点P为斜边AB上一动点，过点P作PE⊥AC于E，PF⊥BC于点F，连结EF，则线段EF的最小值为（ ）
A．24
B．
C．
D．5
4、（4分）下列命题中，错误的是（ ）
A．平行四边形的对角线互相平分
B．菱形的对角线互相垂直平分
C．矩形的对角线相等且互相垂直平分
D．角平分线上的点到角两边的距离相等
5、（4分）若代数式在实数范围内有意义，则x的取值范围是( )
A．x≥﹣2B．x＞﹣2C．x≥2D．x≤2
6、（4分）在直角坐标系中，线段是由线段平移得到的，已知则的坐标为（ ）
A．B．C．D．
7、（4分）下列说法正确的是（ ）
A．四条边相等的平行四边形是正方形
B．一条线段有且仅有一个黄金分割点
C．对角线相等且互相平分的四边形是菱形
D．位似图形一定是相似图形
8、（4分）矩形的边长是，一条对角线的长是，则矩形的面积是（ ）
A．B．C．.D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若正比例函数 y k2x 的图象经过点 A1,  3 ， 则k的值是_____.
10、（4分）若有意义，则的取值范围为_________.
11、（4分）如图，在平面直角坐标系中，点A1，A2，A3…和B1，B2，B3，…分别在直线y＝x+b和x轴上．△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形如果点A1（1，1），那么点A2019的纵坐标是_____．
12、（4分）现有甲、乙两支足球队，每支球队队员身高的平均数均为1.85米，方差分别为，，则身高较整齐的球队是__队
13、（4分）的倒数是_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）为了预防流感，某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中，室内每立方米空气中的含药量y（mg）与时间t（h）成正比；药物释放完毕后，y与t之间的函数解析式为y=（a为常数），如图所示. 根据图中提供的信息，解答下列问题：
（1）写出从释放药物开始，y与t之间的两个函数解析式及相应的自变量取值范围；
（2）据测定，当空气中每立方米的含药量降低到0.25mg以下时，学生方可进入教室，那么药物释放开始，至少需要经过多少小时，学生才能进入教室？
15、（8分）直线y＝x+b与双曲线y＝交于点A（﹣1，﹣5）．并分别与x轴、y轴交于点C、B．
（1）直接写出b＝ ，m＝ ；
（2）根据图象直接写出不等式x+b＜的解集为 ；
（3）若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在，请求出D的坐标；若不存在，请说明理由．
16、（8分）如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，DE，BF与对角线AC分别交于点M，N，连接MF，NE．
（1）求证：DE∥BF
（2）判断四边形MENF是何特殊的四边形？并对结论给予证明；
17、（10分）计算与化简：
（1）化简
（2）化简，
（3）计算
（4）计算
18、（10分）关于x的方程ax2+bx+c=0（a0）.
（1）已知a，c异号，试说明此方程根的情况.
（2）若该方程的根是x1=-1，x2=3，试求方程a（x+2）2+bx+2b+c=0的根.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）将直线向右平移2个单位长度，所得直线的解析式为________．
20、（4分）正八边形的一个内角的度数是 度．
21、（4分）在一个不透明的盒子里装有黑、白两种颜色的球共50只，这些球除颜色外其余完全相同．小颖做摸球实验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中．不断重复上述过程，下表是实验中的一组统计数据：
请估计：当n很大时，摸到白球的频率将会接近_____；（精确到0.1）
22、（4分）如图1，四边形ABCD中，AB∥CD，∠B=90°，AC=AD．动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度匀速运动，在整个运动过程中，△BCP的面积S与运动时间t（秒）的函数图象如图2所示，写出
①AB=__________；
②CD=_______________（提示：过A作CD的垂线）；
③BC=_______________．
23、（4分）方程在实数范围内的解是_____.
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（﹣1，﹣3），C（3，n），交y轴于点B，交x轴于点D．
（1）求反比例函数y＝和一次函数y＝kx+b的表达式；
（2）连接OA，OC．求△AOC的面积．
25、（10分）已知，直线与反比例函数交于点，且点的横坐标为4，过轴上一点作垂直于交于点，如图.
（1）若点是线段上一动点，过点作，，垂足分别于、，求线段长度的最小值.
（2）在（1）的取得最小值的前提下，将沿射线平移，记平移后的三角形为，当时，在平面内存在点，使得、、、四点构成平行四边形，这样的点有几个？直接写出点的坐标.
26、（12分）解不等式组，并写出不等式组的整数解.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据通话时间少于200分钟时，A、B两方案的费用可判断选项A；根据300＜x＜400时，两函数图象可判断选项B；根据月通话费用为70元时，比较图象的横坐标大小即可判断选项C；根据x≤400，根据图象的纵坐标可判断选项D．
【详解】
根据图象可知，当月通话时间低于200分钟时，A方案通话费用始终是30元，B方案通话费用始终是50元，故选项A不合题意；
当300＜x＜400时，A方案通话费用大于70元，B方案通话费用始终是50元，故选项B不合题意；
当月通话费用为70元时，A方案通话费时间为300分钟，B方案通话费时间大于400分钟，故选项C不合题意；
当x≤400时，B方案通话费用始终是50元．故选项D符合题意．
故选D．
本题主要考查了一次函数的应用，根据题意弄清函数图象横纵坐标、函数图象的位置及交点坐标的实际意义是解题的关键．
2、D
【解析】
通过点经过四边形各个顶点，观察图象的对称趋势问题可解.
【详解】
、选项路线都关于对角线对称，因而函数图象应具有对称性，故、错误，对于选项点从到过程中的长也存在对称性，则图象前半段也应该具有对称特征，故错误.
故选：.
本题动点问题的函数图象，考查学生对动点运动过程中所产生函数图象的变化趋势判断.解答关键是注意动点到达临界前后的图象变化.
3、C
【解析】
连接PC，当CP⊥AB时，PC最小，利用三角形面积解答即可．
【详解】
解：连接PC，
∵PE⊥AC，PF⊥BC，
∴∠PEC=∠PFC=∠C=90°，
∴四边形ECFP是矩形，
∴EF=PC，
∴当PC最小时，EF也最小，
即当CP⊥AB时，PC最小，
∵AC=1，BC=6，
∴AB=10，
∴PC的最小值为：=4.1．
∴线段EF长的最小值为4.1．
故选C．
本题主要考查的是矩形的判定与性质，关键是根据矩形的性质和三角形的面积公式解答．
4、C
【解析】
试题分析：根据平行四边形的性质对A进行判断；根据菱形的性质对B进行判断；根据矩形的性质对C进行判断；根据角平分线的性质对D进行判断．
解：A、平行四边形的对角线互相平分，所以A选项的说法正确；
B、菱形的对角线互相垂直平分，所以B选项的说法正确；
C、矩形的对角线相等且互相平分，所以C选项的说法错误；
D、角平分线上的点到角两边的距离相等，所以D选项的说法正确．
故选C．
5、C
【解析】
根据二次根式的性质，被开方数大于等于0，就可以求解．
【详解】
解：根据题意得：x﹣1≥0，
解得：x≥1．
故选：C．
本题考查了二次根式有意义的条件，知识点为：二次根式的被开方数是非负数．
6、B
【解析】
根据点A和点A′的坐标判断出平移方式，根据平移方式可得点的坐标．
【详解】
解：∵点A的坐标为（−2，3），A′的坐标为（3，4），
∴线段AB向上平移1个单位，向右平移5个单位得到线段A′B′，
∵点B的坐标为（−3，1），
∴点B′的坐标为（2，2），
故选：B．
此题主要考查了坐标与图形变化—平移，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
7、D
【解析】
直接利用位似图形的性质以及矩形、菱形的判定方法分别分析得出答案．
【详解】
解：A、四条边相等的平行四边形是菱形，故此选项错误； B、一条线段有且仅有一个黄金分割点不正确，一条线段有两个黄金分割点，故此选项错误； C、对角线相等且互相平分的四边形是矩形，故此选项错误； D、位似图形一定是相似图形，正确．
故选：D．
此题主要考查了位似图形的性质以及矩形、菱形的判定方法，正确掌握相关性质与判定是解题关键．
8、C
【解析】
根据勾股定理求出矩形的另一条边的长度，即可求出矩形的面积.
【详解】
由题意及勾股定理得矩形另一条边为＝＝4
所以矩形的面积＝44＝16.
故答案选C.
本题考查的知识点是勾股定理，解题的关键是熟练的掌握勾股定理.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、-1
【解析】
把A1,  3点代入正比例函数y k2x中即可求出k值.
【详解】
∵正比例函数 y k2x 的图象经过点 A1,  3，
∴，解得：k=-1.
故答案为：-1.
本题考查了正比例函数上点的特征，正确理解正比例函数上点的特征是解题的关键.
10、
【解析】
根式有意义,被开方式要大于等于零.
【详解】
解：∵有意义，
∴2x0,
解得：
故填.
本题考查了根式有意义的条件,属于简单题,熟悉二次根式有意义的条件是解题关键.
11、
【解析】
设点A2，A3，A4…，A1坐标，结合函数解析式，寻找纵坐标规律，进而解题．
【详解】
∵A1（1，1）在直线y=x+b，
∴b=，
∴y=x+，
设A2（x2，y2），A3（x3，y3），A4（x4，y4），…，A1（x1，y1）
则有 y2=x2+，
y3=x3+，
…
y1=x1+．
又∵△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形．
∴x2=2y1+y2，
x3=2y1+2y2+y3，
…
x1=2y1+2y2+2y3+…+2y2+y1．
将点坐标依次代入直线解析式得到：
y2=y1+1
y3=y1+y2+1= y2
y4= y3
…
y1=y2
又∵y1=1
∴y2= y3=（）2
y4=（）3
…
y1=（）2
故答案为（）2．
此题主要考查了 一次函数点坐标特点；等腰直角三角形斜边上高等于斜边长一半；找规律．
12、乙
【解析】
根据方差的定义，方差越小数据越稳定即可得出答案．
【详解】
解：两队队员身高平均数均为1.85米，方差分别为，，
，
身高较整齐的球队是乙队；
故答案为：乙．
本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
13、
【解析】
分析：根据倒数的意义或二次根式的化简进行计算即可.
详解：因为×=1
所以的倒数为.
故答案为.
分析：此题主要考查了求一个数的倒数，关键是明确倒数的意义，乘积为1的两数互为倒数.
三、解答题（本大题共5个小题，共48分）
14、 (1)y＝t（0≤t≤） (2)6小时
【解析】
(1) 将点代入函数关系式, 解得, 有
将代入, 得, 所以所求反比例函数关系式为;
再将代入, 得,所以所求正比例函数关系式为.
(2) 解不等式, 解得,
所以至少需要经过6小时后，学生才能进入教室.
15、（1）-1，2；（2） x＜﹣1或0＜x＜2；（3）存在，D的坐标是（6，0）或（20，0）．
【解析】
（1）把A的坐标分别代入一次函数与反比例函数的解析式，即可求得b和m的值；
（2）根据图象即可直接写出，即反比例函数的图象在一次函数的图象上部的部分x的取值；
（3）求得△OAB的边长，点D在x轴的正半轴上，可以分D在线段OC上（不在O点）或线段OC的延长线上两种情况讨论，依据相似三角形的对应边的比相等即可求得．
【详解】
解：（1）把A（﹣1，﹣2）代入y＝x+b得：﹣2＝﹣1+b，解得：b＝﹣1．
把A（﹣1，﹣2）代入y＝，得：m＝（﹣1）（﹣2）＝2．
故答案是：﹣1，2；
（2）解集为：x＜﹣1或0＜x＜2，
故答案是：x＜﹣1或0＜x＜2；
（3）OA＝＝，
在y＝x﹣1中，令x＝0，解得y＝﹣1，则B的坐标是（0，﹣1）．
令y＝0，解得：x＝1，则C的坐标是（1，0）．
故OB＝1，AB＝＝，BC＝1，OC＝1．
∴OB＝OC，即△OBC是等腰直角三角形，
∴∠OCB＝∠OBC＝12°，∠BCE＝132°．
过A作AF⊥y轴于点F．则△ABF是等腰直角△，∠ABF＝12°，∠ABO＝132°．
1）当D在线段OC（不与O重合）上时，两个三角形一定不能相似；
2）当D在线段OC的延长线上时，设D的坐标是（x，0），则CD＝x﹣1，
∠ABO＝∠BCD＝132°，
当△AOB∽△DBC时，＝，即＝，
解得：x＝6，
则D的坐标是（6，0）；
当△AOB∽△BDC时，，即＝，
解得：x＝20，
则D的坐标是（20，0）．
则D的坐标是（6，0）或（20，0）．
本题是一次函数、反比例函数与相似三角形的判定与性质的综合应用，注意到∠ABO＝∠BCD＝132°是解本题的关键．
16、（1）见解析；（2）平行四边形，证明见解析
【解析】
（1）根据已知条件证明四边形DEBF为平行四边形，即可得到；
（2）证明△FNC≌EMA，得到FN=EM，又FN∥EM，可得结果.
【详解】
解：（1）证明：在平行四边形ABCD中，AB∥CD，AB=CD，
∵E，F分别是AB，CD的中点，
∴DF=BE，DF∥BE，
∴四边形DEBF为平行四边形，
∴DE∥BF；
（2）MENF为平行四边形，理由是：
如图，∵DE∥BF，
∴∠FNC=∠DMC=∠AME，
又∵DC∥AB，
∴∠ACD=∠CAB，又CF=AE=AB=CD，
∴△FNC≌EMA（AAS），
∴FN=EM，又FN∥EM，
∴MENF为平行四边形.
本题考查了平行四边形的性质和判定，本题考查了平行四边形的判定和性质，难度不大，解题的关键是要找到合适的全等三角形.
17、（1）（2）（3）（4）
【解析】
（1）原式变形后，利用同分母分式的减法法则计算即可得到结果．
（2）首先把括号里的式子进行通分，然后把除法运算转化成乘法运算，进行约分化简，最后代值计算，代自己喜欢的值时注意不能使分母为1．
（3）先把各根式化为最简二次根式，再合并同类项即可
（4）二次根式的性质去括号，再合并同类二次根式。
【详解】
（1）.原式
（2）原式
（3）原式
（4）原式
此题考查分式的混合运算， 掌握运算法则是解题关键
18、（1）见解析；（2）x=-3或x=1
【解析】
（1）用一元二次的根判别式判断即可；（2）观察得出a（x+2）2+bx+2b+c=0的解是原方程的解加2，从而解出方程
【详解】
（1）∵△＝b2﹣4ac，
当a、c异号时，即ac＜0，
∴△＝b2﹣4ac＞0，
∴该方程必有两个不相等的实数根；
（2）∵ax2+bx+c=0两根分别为x1=-1，x2=3，
∴方程a（x+2）2+bx+2b+c=a（x+2）2+b(x+2)+c=0中的x+2=-1或x+2=3
解得x=-3或x=1
熟练掌握一元二次方程根的判别式是解决本题的关键，（2）通过两根不能算出啊，b，c的值则要观察题上两方程之间的关系
一、填空题（本大题共5个小题，每小题4分，共20分）
19、y＝−3x＋1
【解析】
根据“上加下减，左加右减”的平移规律进行解答即可．
【详解】
解：由“左加右减”的原则可知，将直线y＝−3x＋1向右平移2个单位长度所得函数的解析式为：y＝−3（x−2）＋1，即y＝−3x＋1，
故答案为：y＝−3x＋1．
本题考查的是一次函数的图象与几何变换，熟知“上加下减，左加右减”的平移规律是解答此题的关键．
20、135
【解析】
根据多边形内角和定理：（n﹣2）•180°（n≥3且n为正整数）求出内角和，然后再计算一个内角的度数即可.
【详解】
正八边形的内角和为：（8﹣2）×180°=1080°，
每一个内角的度数为： 1080°÷8=135°，
故答案为135.
21、0.60
【解析】
计算出平均值即可解答
【详解】
解：由表可知，当n很大时，摸到白球的频率将会接近0.60；
故答案为：0.60；
此题考查利用频率估计概率，解题关键在于求出平均值
22、1 6 2
【解析】
根据图1和图2得当t=1时，点P到达A处，即AB=1；当S=12时，点P到达点D处，即可求解．
【详解】
①当t=1时，点P到达A处，即AB=1．
故答案是：1；
②过点A作AE⊥CD交CD于点E，则四边形ABCE为矩形，
∵AC=AD，
∴DE=CE=，
∴CD=6，
故答案是：6；
③当S=12时，点P到达点D处，则S=CD•BC=（2AB）•BC=1×BC=12，
则BC=2，
故答案是：2．
考查了动点问题的函数图象，注意分类讨论的思想、函数的知识和等腰三角形等的综合利用，具有很强的综合性.
23、
【解析】
由x3+8=0，得x3=-8，所以x=-1．
【详解】
由x3+8=0，得
x3=-8，
x=-1，
故答案为：x=-1．
本题考查了立方根，正确理解立方根的意义是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）y＝，y＝x﹣2；（2）1.
【解析】
（1）先把A点坐标代入y＝中求出m得到反比例函数的解析式是y＝，再确定C的坐标，然后利用待定系数法求一次函数解析式；
（2）先确定D（2，0），然后根据三角形面积公式，利用S△AOC＝S△OCD+S△AOD进行计算．
【详解】
解：（1）把A（﹣1，﹣3）代入y＝得m＝﹣1×（﹣3）＝3，
则反比例函数的解析式是y＝，
当x＝3代入y＝＝1，则C的坐标是（3，1）；
把A（﹣1，﹣3），C（3，1）代入y＝kx+b得，解得，
所以一次函数的解析式是：y＝x﹣2；
（2）x＝0，x﹣2＝0，解得x＝2，则D（2，0），
所以S△AOC＝S△OCD+S△AOD＝×2×（1+3）＝1．
本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了待定系数法求函数解析式．
25、（1）最小值为4.8；（2）这样的点有3个，；；.
【解析】
（1）利用反比例函数图象上点的坐标特征可求出点A的坐标，由点A的坐标，利用待定系数法可求出直线0A的解析式，设点P的坐标为(m,m)(),则PE=m，PF=8-m，利用勾股定理可找出EF2关于m的函数关系式，再利用二次函数的性质，即可求出EF2的最小值，进而可得出段EF长度的最小值；
（2）由(1)的结论结合平移的性质，可得出平移后点、、的坐标.
【详解】
解：（1）当x=4时，
∴
设直线OA的解析式为
将代入得k=
设点P的坐标为(m,m)() 则PE=m，PF=8-m
∴FE2=PF2+PE2即FE2=（m）2+（8-m）2=（m-）2+

∴当m=时，EF2取得最小值，此时EF最小值为
∴最小值为4.8.
（2）这样的点有3个.
；；
本题考查了反比例函数图象上点的坐标特征、待定系数法求解一次函数解析式、勾股定理以及平行四边形的性质等知识点.
26、不等式组的解集是；不等式组的整数解是.
【解析】
先求出两个不等式的解集，再求不等式组的解集，写出其整数解即可.
【详解】
解不等式①得：
解不等式②得：
∴不等式组的解集是
∴不等式组的整数解是.
考查解一元一次不等式组，一元一次不等式组的整数解，熟练掌握解一元一次不等式是解题的关键.
题号
一
二
三
四
五
总分
得分
批阅人
摸球的次数n
100
200
300
500
800
1 000
3 000
摸到白球的次数m
65
124
178
302
481
620
1845
摸到白球的频率
0.65
0.62
0.593
0.604
0.601
0.620
0.615