初中数学人教版（2024）八年级上册12.1 全等三角形教课课件ppt

这是一份初中数学人教版（2024）八年级上册12.1 全等三角形教课课件ppt，共33页。
知识点6　用“斜边、直角边(HL)”判定两个三角形全等
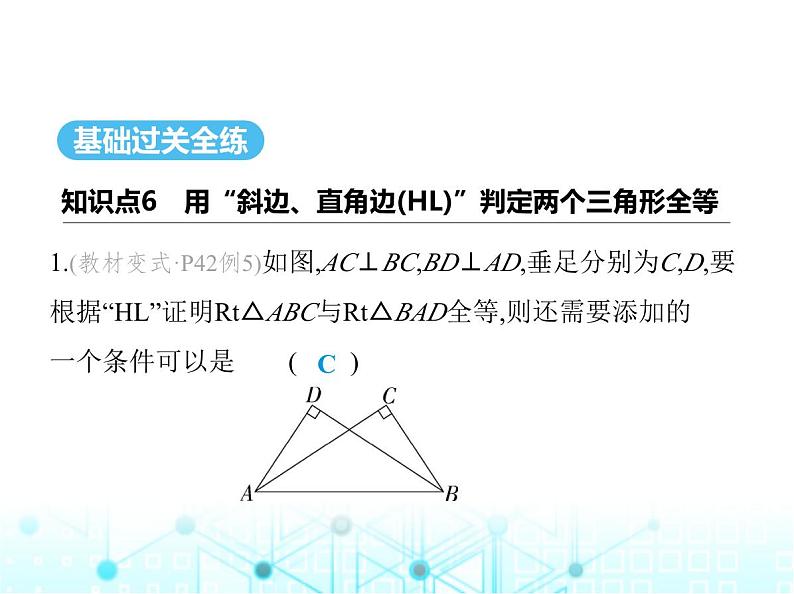
1.(教材变式·P42例5)如图,AC⊥BC,BD⊥AD,垂足分别为C,D,要根据“HL”证明Rt△ABC与Rt△BAD全等,则还需要添加的一个条件可以是　    (　    )
A.∠CAB=∠DBA　　　     B.AB=BDC.BC=AD　　　     D.∠ABC=∠BAD
解析　从题图中可知AB为Rt△ABC和Rt△BAD的斜边,也是 公共边,则根据“HL”证明Rt△ABC≌Rt△BAD,还需添加一 对直角边相等,即BC=AD或AC=BD,故选C.
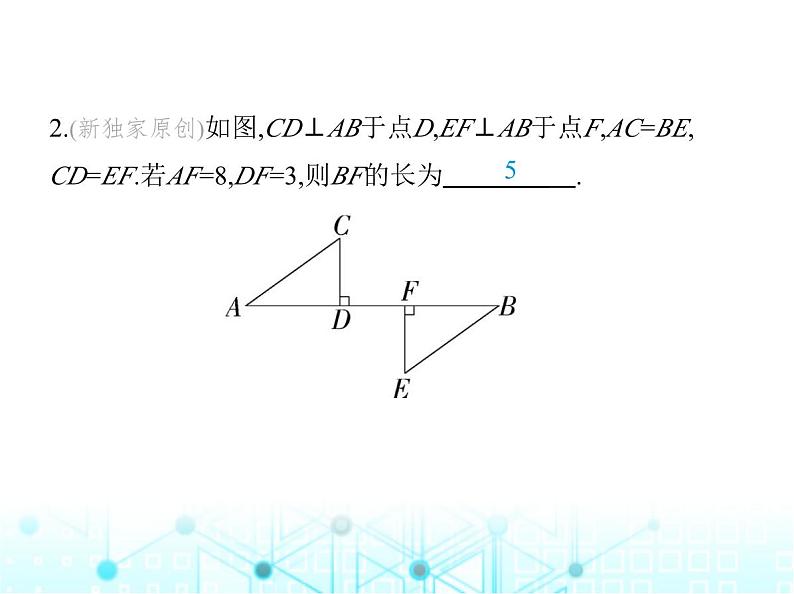
2.(新独家原创)如图,CD⊥AB于点D,EF⊥AB于点F,AC=BE, CD=EF.若AF=8,DF=3,则BF的长为　　　　    . 
解析　∵CD⊥AB,EF⊥AB,AC=BE,CD=EF,∴Rt△ACD≌Rt△BEF(HL),∴AD=BF,∵AF=8,DF=3,∴BF=AD=AF-DF=8-3=5.
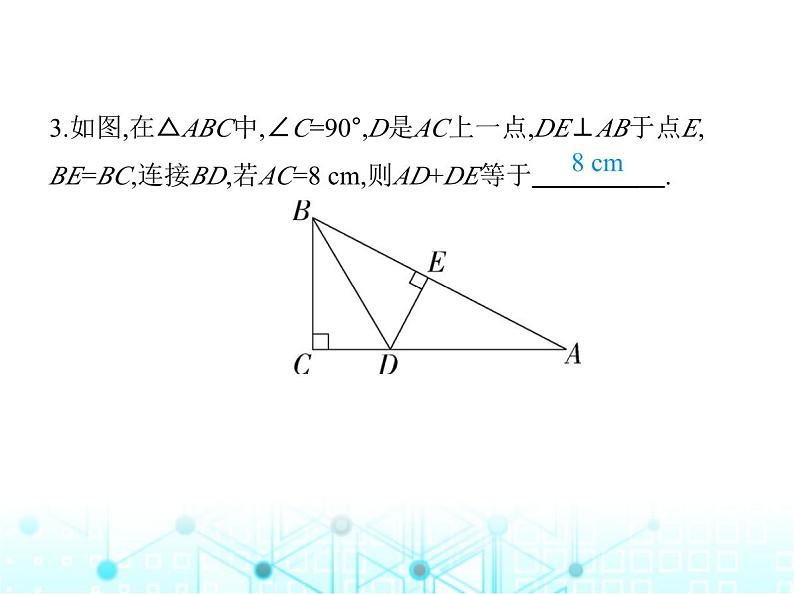
3.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E, BE=BC,连接BD,若AC=8 cm,则AD+DE等于　　　　    . 
解析　∵∠C=90°,DE⊥AB,∴∠C=∠BED=90°,在Rt△BCD和Rt△BED中, ∴Rt△BCD≌Rt△BED(HL),∴CD=DE,∴AD+DE=AD+DC=AC=8 cm.
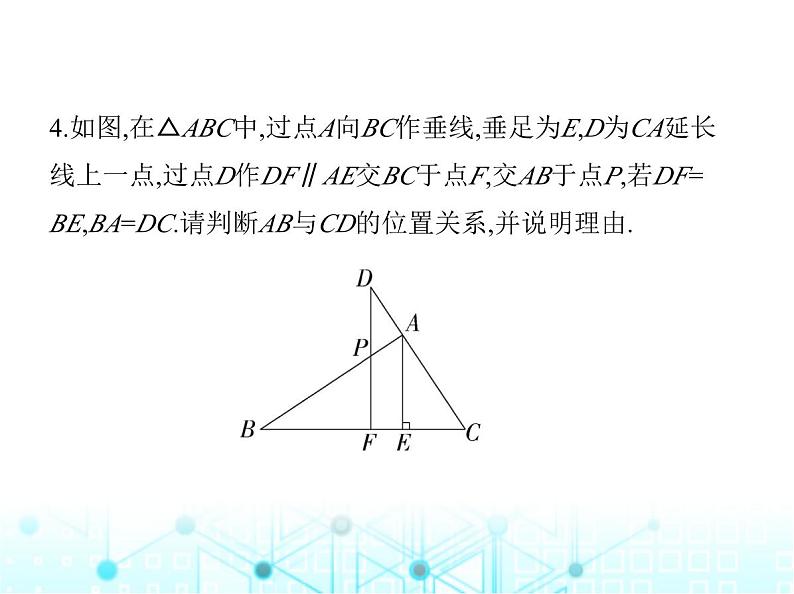
4.如图,在△ABC中,过点A向BC作垂线,垂足为E,D为CA延长 线上一点,过点D作DF∥AE交BC于点F,交AB于点P,若DF= BE,BA=DC.请判断AB与CD的位置关系,并说明理由. 
解析    AB⊥CD.理由如下:∵AE⊥BC,DF∥AE,∴DF⊥BC,∴∠DFC=90°,在Rt△ABE和Rt△CDF中, ∴Rt△ABE≌Rt△CDF(HL),∴∠B=∠D,∵∠BPF=∠APD,∴∠DAP=∠BFD=90°,∴AB⊥CD.
知识点7　全等三角形判定方法的灵活应用
5.(2024山东威海期末)如图,点B,E、C,F在同一条直线上,∠B =∠DEF,∠A=∠D,补充下列条件后不能证明△ABC≌△DEF的是 (　    ) A.AC∥DF　　　 B.AC=DF　    C.BE=CF　　       D.AB=DE
解析　∵∠B=∠DEF,∠A=∠D,∴当添加AC∥DF时,∠ACB =∠F,不能证明△ABC≌△DEF;当添加AC=DF时,△ABC≌ △DEF(AAS);当添加BE=CF时,BC=EF,∴△ABC≌△DEF (AAS);当添加AB=DE时,△ABC≌△DEF(ASA).故选A.
6.(2023山东德州期末)如图,AD=AE,∠1=∠2,请你添加一个 条件:　　　 　     (只填一个即可),使△ABD≌△ACE. 
AB=AC(答案不唯一)
解析　∵∠1=∠2,∴∠1+∠CAD=∠2+∠CAD,即∠BAD=∠CAE.在△ABD与△ACE中,AD=AE,∠BAD=∠CAE,若添加AB=AC, 根据SAS可以判定△ABD≌△ACE(答案不唯一).
7.(一题多解)(截长补短法)如图,在△ABC中,AB>AC,点D在 BC上,∠1=∠2,P为AD上任意一点,连接BP、CP,求证:AB- AC>PB-PC. 
证明　证法一(截长法):如图,在AB上截取AE,使AE=AC,连接 PE, 在△AEP和△ACP中, 
∴△AEP≌△ACP(SAS),∴PE=PC,在△PBE中,BE>PB-PE,即AB-AC>PB-PC.证法二(补短法):如图,延长AC到E,使AE=AB,连接PE, 
在△AEP和△ABP中, ∴△AEP≌△ABP(SAS),∴PE=PB,在△PCE中,CE>PE-PC,即AB-AC>PB-PC.
8.(2023黑龙江牡丹江中考,14,★☆☆)如图,AB∥CD,AD与BC交于点O,请添加一个条件:　　 　　     ,使△AOB≌△DOC.(只填一种即可) 
AB=DC(答案不唯一)
解析　∵AB∥CD,∴∠A=∠D,∠B=∠C,∴添加AB=DC,由ASA可证明△AOB≌△DOC.(答案不唯一)
9.(2024山东青岛二十六中月考,15,★★☆)如图,在△ABC中, AD,BE分别是BC,AC边上的高,已知AE=BD,若∠CAB=60°,则 ∠CBE的度数为　　　　    . 
解析　∵AD,BE分别是BC,AC边上的高,∴BE⊥AC,AD⊥BC,在Rt△AEB和Rt△BDA中, ∴Rt△AEB≌Rt△BDA(HL),∴∠EAB=∠DBA=60°,∵∠AEB=90°,∴∠ABE=30°,∴∠CBE=∠ABD-∠ABE=60°-30°=30°.
10.(2022湖南长沙中考,21,★★☆)如图,AC平分∠BAD,CB⊥ AB,CD⊥AD,垂足分别为B,D.(1)求证:△ABC≌△ADC.(2)若AB=4,CD=3,求四边形ABCD的面积. 
解析    (1)证明:∵AC平分∠BAD,∴∠BAC=∠DAC,∵CB⊥AB,CD⊥AD,∴∠B=∠D=90°,在△ABC和△ADC中, ∴△ABC≌△ADC(AAS).(2)由(1)知△ABC≌△ADC,∴BC=CD=3,S△ABC=S△ADC,∴S△ABC= AB·BC= ×4×3=6,∴S△ADC=6,
∴S四边形ABCD=S△ABC+S△ADC=12.
11.(2022河南郑州中学期中,20,★★☆)如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.(1)求证:BD=BC.(2)若BD=6 cm,求AC的长. 
解析    (1)证明:∵DE⊥AB,∴∠BFE=90°,∴∠ABC+∠DEB=90°,∵∠ACB=90°,∴∠ABC+∠A=90°,∴∠A=∠DEB,在△ABC和△EDB中, ∴△ABC≌△EDB(AAS),∴BD=BC.(2)由(1)知△ABC≌△EDB,∴AC=BE,BC=BD=6 cm,∵E是BC的中点,∴BE=  BC=3 cm,∴AC=3 cm.
12.(几何直观)如图,△ABC中,∠ABC=60°,AD、CE分别平分 ∠BAC、∠ACB,AD、CE相交于点P.(1)求∠APC的度数.(2)若AE=3,CD=4,求线段AC的长. 
解析    (1)∵∠ABC=60°,∴∠BAC+∠ACB=120°,∵AD、CE分别平分∠BAC、∠ACB,∴∠PAC+∠PCA= (∠BAC+∠ACB)=60°,∴∠APC=180°-(∠PAC+∠PCA)=120°.(2)如图,在AC上截取AF,使AF=AE,连接PF, 
∵AD平分∠BAC,∴∠BAD=∠CAD,在△APE和△APF中, ∴△APE≌△APF(SAS),∴∠APE=∠APF,∵∠APC=120°,∴∠APE=60°,∠CPD=60°,∴∠APF=60°,∴∠CPF=60°=∠CPD,
∵CE平分∠ACB,∴∠ACP=∠BCP,在△CPF和△CPD中, ∴△CPF≌△CPD(ASA),∴CF=CD,∴AC=AF+CF=AE+CD=3+4=7.
13.(模型观念)如图①,AB=4 cm,AC⊥AB,BD⊥AB,AC=BD=3 cm.点P在线段AB上以1 cm/s的速度由点A向点B运动,同时, 点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP 与△BPQ是否全等?请说明理由,并判断此时线段PC和线段 PQ的位置关系.(2)如图②,将题干中的“AC⊥AB,BD⊥AB”改为“∠CAB= ∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是 否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的
x、t的值;若不存在,请说明理由.  图①　     图②
解析    (1)△ACP≌△BPQ.理由如下:当t=1时,AP=BQ=1 cm,∴BP=3 cm=AC,在△ACP和△BPQ中, ∴△ACP≌△BPQ(SAS),∴∠ACP=∠BPQ,∴∠APC+∠BPQ=∠APC+∠ACP=90°,∴∠CPQ=90°,即线段PC与线段PQ垂直.(2)存在.①若△ACP≌△BPQ,则AC=BP,AP=BQ,