初中人教版（2024）13.3.1 等腰三角形授课ppt课件

这是一份初中人教版（2024）13.3.1 等腰三角形授课ppt课件，共32页。
知识点1　等腰三角形的性质
1.(2023江苏宿迁中考)若等腰三角形有一个内角为110°,则这 个等腰三角形的底角是 (　    )A.70°　　　    B.45°　　　    C.35°　　　    D.50°
2.(教材变式·P77T3)如图,在△ABC中,AB=AD,∠B=2∠C,∠BAD=32°,则∠C的度数为 (　    ) A.32°　　　    B.35°　　　    C.37°　　　    D.40°
3.(2020甘肃兰州中考)如图,在△ABC中,AB=AC,点D在CA的 延长线上,DE⊥BC于点E,∠BAC=100°,则∠D= (　    ) A.40°　　　    B.50°　　　    C.60°　　　    D.80°
解析　∵AB=AC,∠BAC=100°,∴∠C=∠B=40°,∵DE⊥BC,∴∠D=90°-∠C=50°.故选B.
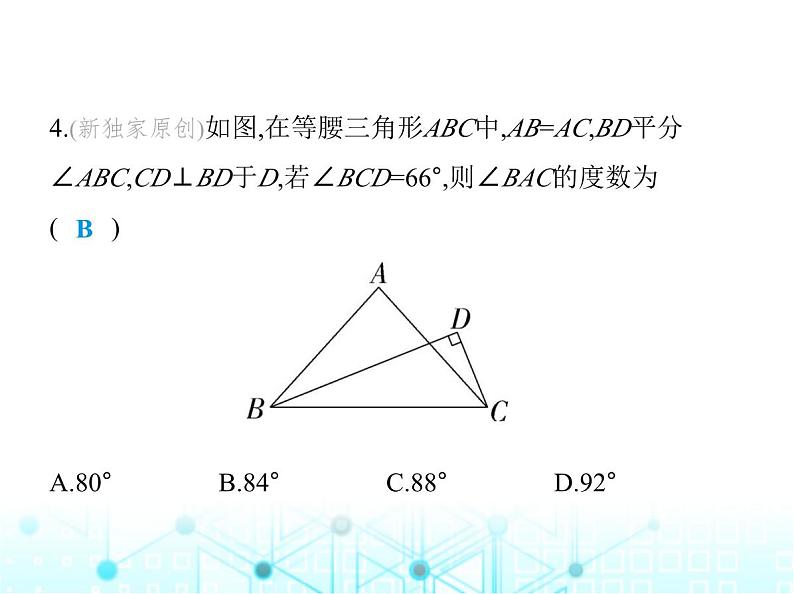
4.(新独家原创)如图,在等腰三角形ABC中,AB=AC,BD平分∠ABC,CD⊥BD于D,若∠BCD=66°,则∠BAC的度数为 (　    ) A.80°　　　    B.84°　　　    C.88°　　　    D.92°
解析　∵CD⊥BD,∴∠BDC=90°,∴∠DBC+∠BCD=90°,∵∠BCD=66°,∴∠DBC=24°,∵BD平分∠ABC,∴∠ABC=2∠DBC=48°,∵AB=AC,∴∠ACB=∠ABC=48°,∴∠BAC=180°-∠ABC-∠ACB=84°.故选B.
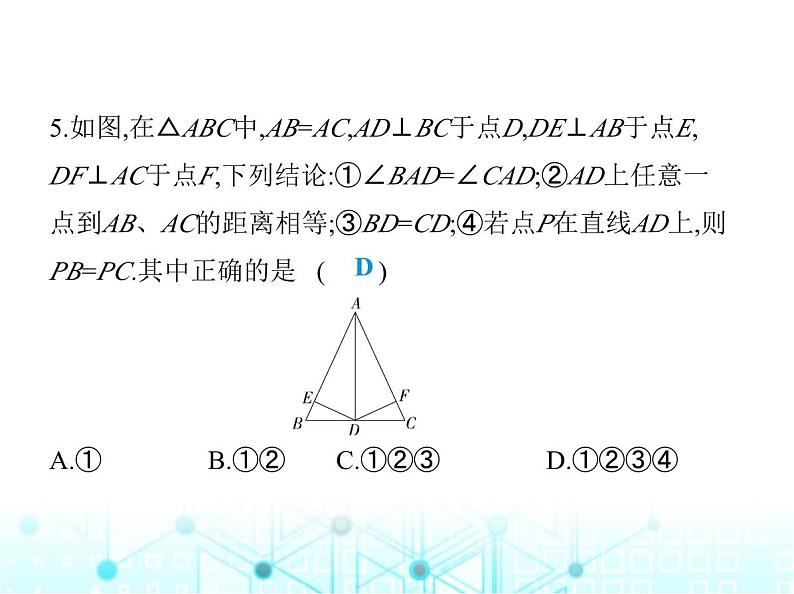
5.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E, DF⊥AC于点F,下列结论:①∠BAD=∠CAD;②AD上任意一 点到AB、AC的距离相等;③BD=CD;④若点P在直线AD上,则 PB=PC.其中正确的是 (　    ) A.①　　　    B.①②C.①②③　　　    D.①②③④
解析　∵AB=AC,∴△ABC是等腰三角形,∵AD⊥BC,∴∠BAD=∠CAD,BD=CD,故①③正确;∵∠BAD=∠CAD,∴AD上任意一点到AB、AC的距离相等,故②正确;∵AD⊥BC,BD=CD,∴AD垂直平分BC,∵点P在直线AD上,∴PB=PC,故④正确.故选D.
6.(易错题)若等腰三角形中有一个角等于40°,则这个等腰三 角形顶角的度数为　　　　     .
解析　∵等腰三角形中有一个角等于40°,∴①若40°为顶角,则这个等腰三角形的顶角的度数为40°;②若40°为底角,则这个等腰三角形的顶角的度数为180°-40°×2=100°.∴这个等腰三角形顶角的度数为40°或100°.
易错警示    本题的易错之处是忽略分类讨论,因为题中没有指明该内角 是顶角还是底角,所以要分两种情况进行讨论.
7.如图,在△ABC中,AB=AC,∠B=25°,点D在线段BA的延长线 上,点E在AC上,连接DE,且AE=DE,点F在BC上,连接DF,且BF =DF,则∠EDF的度数为　　　　    . 
解析　∵AB=AC,∴∠C=∠B=25°.∴∠EAD=∠B+∠C=50°.∵AE=DE,∴∠EDA=∠EAD=50°.∵BF=DF,∴∠FDB=∠B=25°,∴∠EDF=∠EDA-∠FDB=50°-25°=25°.
8.(2023安徽芜湖一中月考)如图,在△ABC中,D为AB上一点, E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数 为　　　　    . 
解析　∵AC=CD=BD=BE,∠A=40°,∴∠CDA=∠A=40°,∠B=∠DCB,∠BDE=∠BED,∵∠B+∠DCB=∠CDA=40°,∴∠B=20°,∵∠B+∠BDE+∠BED=180°,∴∠BDE=∠BED= ×(180°-20°)=80°,∴∠CDE=180°-∠CDA-∠BDE=60°.
9.如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,连接 AD,BE.若AD,BE分别是△ABC的中线和角平分线,∠CAD=20°,求∠CBE的度数. 
解析　∵AB=AC,AD是△ABC的中线,∴∠BAD=∠CAD=20°,∠ABC=∠ACB,∴∠ABC= ×(180°-20°-20°)=70°,∵BE是△ABC的角平分线,∴∠CBE= ∠ABC=35°.
10.(方程思想)如图,在△ABC中,点D在BC上,AB=AC=CD,且 AD=BD.求△ABC的三个内角的度数. 
解析　设∠B=x,∵AB=AC,∴∠C=∠B=x,∵AD=BD,∴∠BAD=∠B=x,由三角形外角的性质得∠CDA=∠B+∠BAD=2x,∵AC=CD,∴∠CAD=∠CDA=2x,∵∠C+∠CAD+∠CDA=180°,∴x+2x+2x=180°,解得x=36°,∴∠C=36°,∠B=36°,∴∠BAC=180°-36°-36°=108°.∴△ABC的三个内角的度数分别是108°,36°,36°.
11.(2022山东泰安中考,5,★★☆)如图,l1∥l2,点A在直线l1上, 点B在直线l2上,AB=BC,∠C=25°,∠1=60°,则∠2的度数是 (　    ) A.70°　　　    B.65°　　　    C.60°　　　    D.55°
解析　如图,设直线l2交AC于点E,∵AB=BC,∠C=25°,∴∠BAC=∠C=25°.∵l1∥l2,∠1=60°,∴∠EBA=∠1=60°,∴∠BEC=∠EBA+∠BAC=60°+25°=85°,∴∠2=180°-∠C-∠BEC=180°-25°-85°=70°. 
12.(情境题·数学文化)(2019浙江衢州中考,7,★★☆)“三等 分角”大约是在公元前5世纪由古希腊人提出来的,借助如 图所示的“三等分角仪”能三等分任一角.这个三等分角仪 由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转 动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 (　    )A.60°　　　    B.65°C.75°　　　    D.80°
解析　∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,∴∠DEC=∠DCE=∠O+∠ODC=2∠ODC,∴∠O+∠DEC=3∠ODC=∠BDE=75°,∴∠ODC=25°,∵∠CDE+∠ODC=180°-∠BDE=105°,∴∠CDE=105°-25°=80°.故选D.
13.(2023青海西宁中考,16,★★☆)在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是　　　　    .
解析　∵AB=AC,∠BAC=100°,∴∠B=∠C= (180°-∠BAC)=40°,∵△ABD为直角三角形,∴分两种情况讨论,①∠ADB=90°;②∠BAD=90°,∴∠ADB=90°-∠B=90°-40°=50°.∴∠ADB的度数是90°或50°.
14.(2023辽宁锦州中考,13,★★☆)如图,在△ABC中,BC的垂 直平分线交BC于点D,交AB于点E,连接CE.若CE=CA,∠ACE =40°,则∠B的度数为　　　　    . 
解析　∵CE=CA,∴∠A=∠AEC,∵∠A+∠AEC+∠ACE=180°,∠ACE=40°,∴∠AEC= ×(180°-40°)=70°,∵DE是BC的垂直平分线,∴BE=CE,∴∠B=∠BCE,∵∠AEC=∠B+∠BCE,∴∠B=35°.
15.(新考法)(2024山西太原十五中月考,17,★★★)如图,已知 ∠BAC=80°,A1,B1分别是射线AC,线段A1B上的点,且A1B=AB,A2,B2分别是射线A1C,线段A2B1上的点,且A1A2=A1B1,以此类推.(1)根据上述条件,∠A3A4B3的度数为   　　　 .(2)∠An-1AnBn-1(n≥2)的度数为　　　　    .
解析    (1)∵A1B=AB,∠BAC=80°,∴∠AA1B=∠BAC=80°,∵A1A2=A1B1,∴∠A1A2B1=∠A1B1A2= ×80°=40°,同理,∠A2A3B2=∠A2B2A3= ×40°=20°,∠A3A4B3=∠A3B3A4= ×20°=10°.(2)∵∠A1A2B1=∠A1B1A2= ×80°=40°,∠A2A3B2=∠A2B2A3= ×40°= ×80°=20°,
∠A3A4B3=∠A3B3A4= ×20°= ×80°=10°,……∴∠An-1AnBn-1(n≥2)的度数为 ×80°.
16.(2024河南郑州五十七中期末,21,★★★)已知:如图,在△ABC中,AB=AC,点D是边BC上一点,点E是AC上一点,且AD=AE.(1)若∠BAD=30°,求∠EDC的度数.(2)若∠BAD=α,∠EDC=β,猜想α和β的关系. 
解析    (1)∵AB=AC,∴∠B=∠C,∵AD=AE,∴∠ADE=∠AED,∵∠AED是△CDE的一个外角,∴∠AED=∠C+∠EDC,∴∠ADE=∠C+∠EDC,∵∠ADC是△ABD的一个外角,∴∠ADC=∠B+∠BAD,∵∠ADC=∠ADE+∠EDC,∴∠ADC=∠C+2∠EDC,∴∠C+2∠EDC=∠B+∠BAD,