




还剩50页未读,
继续阅读
所属成套资源:全套鲁教版八年级数学上册课时课件
成套系列资料,整套一键下载
鲁教版八年级数学上册第五章平行四边形素养综合检测课件
展开
这是一份鲁教版八年级数学上册第五章平行四边形素养综合检测课件,共58页。
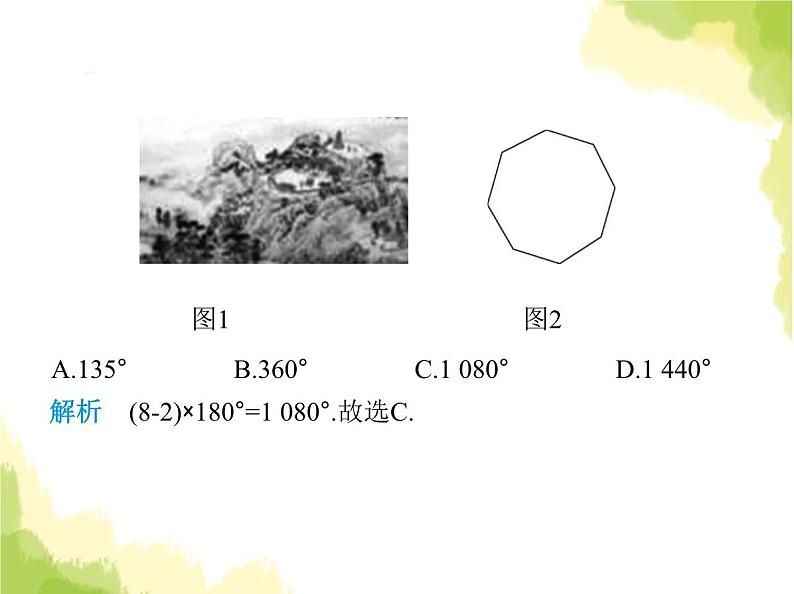
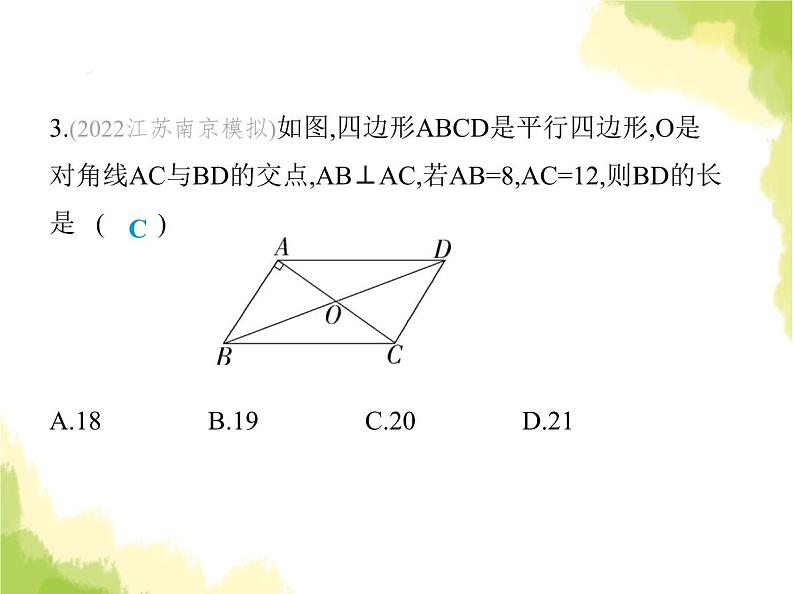
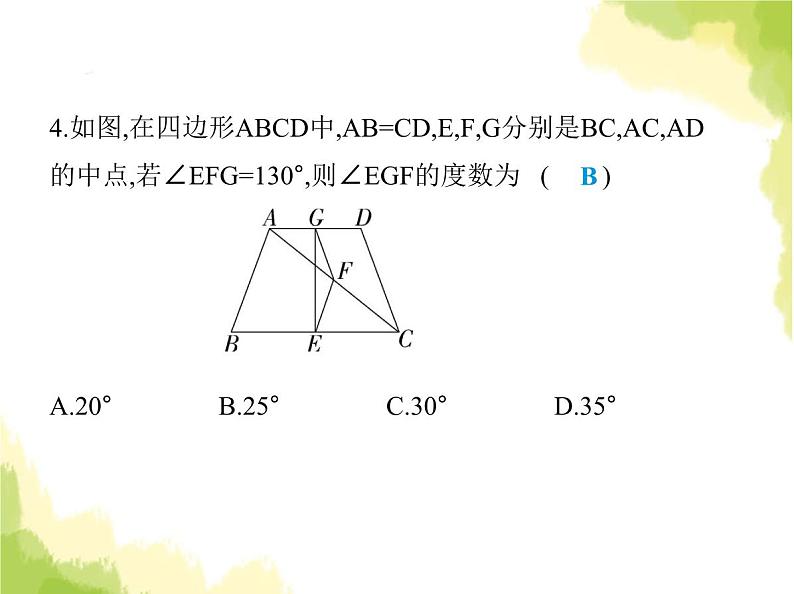
第五章 素养综合检测(满分100分, 限时60分钟)1.(跨学科·历史)(2024重庆綦江期末)图1是被称作“通州八 景”之一的燃灯佛舍利塔,它巍峨挺拔,雄伟壮观,始建于北 周年间,是北京地区建造年代最早、最高大的佛塔之一.燃灯 佛舍利塔为八角形十三层砖木结构密檐式塔,十三层均为正 八边形砖木结构,如图2所示的正八边形是其中一层的平面 示意图,其内角和为 ( )一、选择题(每小题3分,共30分)C 图1 图2A.135° B.360° C.1 080° D.1 440°解析 (8-2)×180°=1 080°.故选C.2.(2023浙江温州瑞安开学测试)在▱ABCD中,∠A+∠C=220°,则∠D的度数是 ( )A.70° B.80° C.90° D.110°A解析 ∵四边形ABCD是平行四边形,∴∠A=∠C,AB∥CD, ∴∠A+∠D=180°,∵∠A+∠C=220°,∴∠A=∠C=110°,∴∠D=180°-∠A=70°.故选A.3.(2022江苏南京模拟)如图,四边形ABCD是平行四边形,O是 对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长 是 ( ) A.18 B.19 C.20 D.21C 解析 ∵四边形ABCD是平行四边形,AC=12,∴OA= AC=6,BD=2OB,∵AB⊥AC,AB=8,∴OB= =10,∴BD=2OB=20.故选C.4.如图,在四边形ABCD中,AB=CD,E,F,G分别是BC,AC,AD 的中点,若∠EFG=130°,则∠EGF的度数为 ( ) A.20° B.25° C.30° D.35°B解析 ∵E,F,G分别是BC,AC,AD的中点,∴EF,GF分别是△ABC,△ADC的中位线,∴EF= AB,GF= CD,∵AB=CD,∴EF=GF,又∵∠EFG=130°,∴∠EGF=∠GEF= =25°,故选B.5.(2023重庆沙坪坝一中月考)如图,在平行四边形ABCD中,E 为线段BC上一点,连接AE,若AE=DC且∠D=60°,则∠BAE= ( ) A.65° B.55° C.50° D.60°D解析 ∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D= 60°,∵AE=CD,∴AE=AB,∴△ABE是等边三角形,∴∠BAE= 60°,故选D.6.(2024贵州遵义播州期末)如图,∠1、∠2、∠3,∠4是六边 形ABCDEF的四个外角,延长FA,CB交于点H.若∠1+∠2+∠ 3+∠4=224°,则∠AHB的度数为 ( ) A.24° B.34° C.44° D.54°C 解析 ∵多边形的外角和都为360°,即∠1+∠2+∠3+∠4+∠HAB+∠ABH=360°,∠1+∠2+∠3+∠4=224°,∴∠HAB+∠ABH=136°.∵∠AHB+∠HAB+∠ABH=180°,∴∠AHB=44°. 故选C.7.(2023河南安阳二模)如图,▱ABCD中,AB=3,BE平分∠ABC,交AD于点E,连接CE,DE=2,点F,G分别是BE,CE的中点, 则FG的长为 ( ) A.3 B.2.5 C.2 D.5B解析 ∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC, ∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ AEB=∠ABE,∴AB=AE=3,∴BC=AD=AE+ED=3+2=5,∵点F,G分别是BE, CE的中点,∴FG是△BEC的中位线,∴FG= BC=2.5,故选B.8.(2023山东东营广饶期末)如图,在▱ABCD中,E,F是对角线 BD上的两点,则添加以下条件不能判定四边形AECF为平行 四边形的是 ( ) A.BE=DF B.AF⊥BD,CE⊥BDC.∠BAE=∠DCF D.AF=CE解析 如图,连接AC,与BD相交于点O, ∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.A.∵BE=DF,∴OB-BE=OD-DF,即OE=OF,∴四边形AECF是 平行四边形;B.∵AF⊥BD,CE⊥BD,∴∠AFD=∠CEB=90°,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADF=∠CBE, ∴△ADF≌△CBE(AAS),∴DF=BE,由A知四边形AECF是平 行四边形;C.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠ ABE=∠CDF,又∵∠BAE=∠DCF,∴△ABE≌△CDF(ASA), ∴BE=DF,由A知四边形AECF是平行四边形;D.由AF=CE不能得到△ADF≌△CBE,无法判定四边形 AECF是平行四边形.故选D.9.(2022辽宁阜新期末)如图,在四边形ABCD中,AB=CD,对角 线AC,BD交于点O,AF⊥BD于点F,CE⊥BD于点E,连接AE, CF.若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形 ABCD是平行四边形;④图中共有4对全等三角形.其中正确的是 ( )A.①③④ B.①②④ C.①②③ D.②③④C 解析 在Rt△DCE和Rt△BAF中, ∴Rt△DCE≌Rt△BAF(HL),∴CE=AF,∵CE⊥BD,AF⊥BD, ∴CE∥AF,∴四边形AECF是平行四边形,∴CF=AE,故①正 确;∵四边形AECF是平行四边形,∴OE=OF,故②正确;∵DE =BF,∴DE-EF=BF-EF,即DF=BE,∴DF+OF=BE+OE,即DO= BO,∵四边形AECF是平行四边形,∴AO=CO,∴四边形ABCD是平行四边形,故③正确;由题意可得△DCF≌△BAE,△CDO≌△ABO,△CDE≌△ABF,△DCB≌△ BAD,△CFO≌△AEO,△CFB≌△AED,△CFE≌△AEF,△ CEO≌△AFO,△ADF≌△CBE,△DOA≌△BOC,△DCA≌ △BAC,△AFC≌△CEA,共12对全等三角形,故④错误.∴正 确的结论是①②③,故选C.10.(手拉手模型)(2022山东济宁任城期末)如图,在△ABC中, AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形, 下列结论:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8,其中错误的个数是 ( ) A.1 B.2 C.3 D.4A解析 ∵AB=3,AC=4,BC=5,32+42=52,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∴AB⊥AC,故①结论正确;∵△ABD,△ACE都是等边三角形,∴∠DAB=∠EAC=60°,∴∠DAE=360°-90°-60°-60°=150°,∵△ABD和△FBC都是等边三角形,∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,∴ ∠DBF=∠ABC,在△ABC和△DBF中, ∴△ABC≌△DBF(SAS),∴AC=DF=4,∵△ACE是等边三角形,∴AE=AC=4,∴DF=AE,同理可证△ABC≌△EFC(SAS),∴AB=EF,∵△ABD是等边三角形,∴AB=AD=3,∴EF=AD,∴四边形AEFD是平行四边形,故②结论正确;∵四边形AEFD是平行四边形,∴∠DFE=∠DAE=150°,故③结论正确;如图,过A作AG⊥DF于G,则∠AGD=90°,∵四边形AEFD是平行四边形,∴AD∥EF,∴∠FDA=180°-∠DFE=180°-150°=30°,∴AG= AD= ,∴S▱AEFD=DF·AG=4× =6,故④结论错误.∴错误结论的个数是1,故选A.二、填空题(每小题3分,共24分)11.(方程思想)(2022山东菏泽中考)若正n边形的一个内角与 一个外角度数的比是3∶2,则n= .5解析 正n边形的各个内角都相等,各个外角也都相等.设一 个外角的度数为2x,则与它相邻的内角的度数为3x,则2x+3x=180°,解得x=36°,∴2x=72°,∵正n边形的外角和为360°,∴n=360°÷72°=5,故答案为5.12.(新考向·开放性试题)(2024黑龙江绥化期末)如图,在四边 形ABCD中,AB∥CD,若添加AD∥BC,则四边形ABCD为平 行四边形.现在请你添加一个适当的条件: ,使得四边形AECF为平行四边形.(图中不再添加点和线)BE=DF(答案不唯一)解析 添加的条件:BE=DF.证明:∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF,又∵BE=DF,∴△ABE≌△CDF(SAS),∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠EFC,∴AE∥FC,∴四边形AECF为平行四边形.故答案为BE=DF.(答案不唯一)13.如图,已知P是▱ABCD的边BC上一点,连接AP,DP,如果 AB=AD=AP,∠B=80°,那么∠CDP的度数为 .30°解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=80°,AD∥BC,∴∠PAD=∠APB,∵AB=AP,∴∠APB=∠B=80°,∴∠PAD=80°,∵AP=AD,∴∠ADP=∠APD=(180°-80°)÷2=50°,∴∠CDP=∠ADC-∠ADP=80°-50°=30°.14.(2023河南商丘永城期末)如图,五边形ABCDE是正五边 形,且l1∥l2.若∠1=57°,则∠2= .129°解析 如图,过点B作BF∥l2交DE于点F, ∵l1∥l2,∴BF∥l1,∵五边形ABCDE是正五边形,∴∠ABC= =108°,∵BF∥l1,∠1=57°,∴∠ABF=∠1=57°,∴∠CBF=∠ABC-∠ABF=108°-57°=51°,∵BF∥l2,∴∠2+∠CBF=180°,∴∠2=180°-51°=129°,故答案为129°.15.(易错题)(2023山东烟台莱州期末)如图,在8×8的正方形网 格中,每个小正方形的顶点称为格点,其中点A,B,C均在格点 上,若点A的坐标为(0,0),点B的坐标为(2,-1),请在给定的网格 中找出格点E,使以A、B、C、E为顶点的四边形是平行四边 形,则点E的坐标为 .(-1,-1)或(1,1)或(5,-1)解析 本题有三种情况.根据题意建立平面直角坐标系,如图所示. 故点E的坐标为(-1,-1)或(1,1)或(5,-1).16.(2023山东威海荣成校级期末)如图,平行四边形ABCD中, AC、BD相交于点O,OE⊥AC交边BC于E,连接AE,若∠ABC =60°,∠BAE=∠DAC,则∠BAE= .40°解析 ∵四边形ABCD是平行四边形,∴AD∥BC,AO=CO,∴∠DAC=∠ACB,∠ABC+∠BAD=180°,∴∠BAD=180°-∠ABC=120°,∵OE⊥AC,∴AE=EC,∴∠CAE=∠ACE,∵∠BAE=∠DAC,∴∠BAE=∠DAC=∠EAC,∴∠BAE=40°.17.小明计算一个多边形的内角和时误把一个外角加进去了, 得其和为2 260°,则这个多边形的边数为 .14解析 设这个多边形的边数为n,多加的一个外角的度数为α, 则(n-2)·180°=2 260°-α,∵内角和是180°的整数倍,0°<α<180°,且2 260°=12×180°+100°,∴小明多加的一个外角的度数为100°,这个多边形的边数为 12+2=14.18.如图,在△ABC中,∠C=90°,D为BC的中点,DE⊥BC,交AB 于点O,BE∥AD,连接AE.以下结论:①四边形ACDE是平行四 边形;②OE=OD;③S四边形ACBE=3S△ACD.其中正确的结论是 .(写出所有正确结论的序号)①②③解析 ∵D为BC的中点,∴BD=CD,∵DE⊥BC,∠C=90°,∴∠BDE=∠C=90°,∴DE∥AC,∵BE∥AD,∴∠EBD=∠ADC,∴△BDE≌△DCA(ASA),∴DE=AC,∴四边形ACDE是平行四边形,故①正确;∵△BDE≌△DCA,∴BE=AD,∵BE∥AD,∴四边形ADBE是平行四边形,∴OE=OD,故②正确;∵四边形ACBE的面积=四边形BDAE的面积+△ACD的面积 =BD·DE+ DC·AC=DC·AC+ DC·AC= DC·AC=3× DC·AC=3S△ACD,∴S四边形ACBE=3S△ACD,故③正确.综上所述,正确的结论 是①②③,故答案为①②③.三、解答题(共46分)19.(2024山东临沂期中)(10分)阅读小明和小红的对话,解决 下列问题. (1)通过列方程说明“多边形的内角和不可能是1 470°”.(2)求该多边形的内角和.(3)若这是一个正多边形,求该正多边形的一个内角比一个外 角大多少.解析 (1)设多边形的边数为n.由题意得(n-2)·180°=1 470°,解得n=10 .∵n为正整数,∴多边形的内角和不可能为1 470°.(2)设这个多边形的边数为n,多加的锐角为α(0°<α<90°),由题 意得(n-2)·180°=1 470°-α,∴0).(1)当点P运动t s时,线段PD的长度为 cm;当点P运动
2 s时,线段BQ的长度为 cm;当点P运动5 s时,线段BQ
的长度为 cm.(2)若经过t s,以P、D、Q、B四点为顶点的四边形是平行四(15-t)75边形,请求出t的值.解析 (1)由题意得AP=t cm,∴PD=(15-t)cm,当点P运动2 s时,CQ=2×4=8(cm),∴BQ=15-8=7(cm),当点P运动5 s时,BQ=4×5-15=5(cm).故答案为(15-t);7;5.(2)由题意知0
第五章 素养综合检测(满分100分, 限时60分钟)1.(跨学科·历史)(2024重庆綦江期末)图1是被称作“通州八 景”之一的燃灯佛舍利塔,它巍峨挺拔,雄伟壮观,始建于北 周年间,是北京地区建造年代最早、最高大的佛塔之一.燃灯 佛舍利塔为八角形十三层砖木结构密檐式塔,十三层均为正 八边形砖木结构,如图2所示的正八边形是其中一层的平面 示意图,其内角和为 ( )一、选择题(每小题3分,共30分)C 图1 图2A.135° B.360° C.1 080° D.1 440°解析 (8-2)×180°=1 080°.故选C.2.(2023浙江温州瑞安开学测试)在▱ABCD中,∠A+∠C=220°,则∠D的度数是 ( )A.70° B.80° C.90° D.110°A解析 ∵四边形ABCD是平行四边形,∴∠A=∠C,AB∥CD, ∴∠A+∠D=180°,∵∠A+∠C=220°,∴∠A=∠C=110°,∴∠D=180°-∠A=70°.故选A.3.(2022江苏南京模拟)如图,四边形ABCD是平行四边形,O是 对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长 是 ( ) A.18 B.19 C.20 D.21C 解析 ∵四边形ABCD是平行四边形,AC=12,∴OA= AC=6,BD=2OB,∵AB⊥AC,AB=8,∴OB= =10,∴BD=2OB=20.故选C.4.如图,在四边形ABCD中,AB=CD,E,F,G分别是BC,AC,AD 的中点,若∠EFG=130°,则∠EGF的度数为 ( ) A.20° B.25° C.30° D.35°B解析 ∵E,F,G分别是BC,AC,AD的中点,∴EF,GF分别是△ABC,△ADC的中位线,∴EF= AB,GF= CD,∵AB=CD,∴EF=GF,又∵∠EFG=130°,∴∠EGF=∠GEF= =25°,故选B.5.(2023重庆沙坪坝一中月考)如图,在平行四边形ABCD中,E 为线段BC上一点,连接AE,若AE=DC且∠D=60°,则∠BAE= ( ) A.65° B.55° C.50° D.60°D解析 ∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D= 60°,∵AE=CD,∴AE=AB,∴△ABE是等边三角形,∴∠BAE= 60°,故选D.6.(2024贵州遵义播州期末)如图,∠1、∠2、∠3,∠4是六边 形ABCDEF的四个外角,延长FA,CB交于点H.若∠1+∠2+∠ 3+∠4=224°,则∠AHB的度数为 ( ) A.24° B.34° C.44° D.54°C 解析 ∵多边形的外角和都为360°,即∠1+∠2+∠3+∠4+∠HAB+∠ABH=360°,∠1+∠2+∠3+∠4=224°,∴∠HAB+∠ABH=136°.∵∠AHB+∠HAB+∠ABH=180°,∴∠AHB=44°. 故选C.7.(2023河南安阳二模)如图,▱ABCD中,AB=3,BE平分∠ABC,交AD于点E,连接CE,DE=2,点F,G分别是BE,CE的中点, 则FG的长为 ( ) A.3 B.2.5 C.2 D.5B解析 ∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC, ∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ AEB=∠ABE,∴AB=AE=3,∴BC=AD=AE+ED=3+2=5,∵点F,G分别是BE, CE的中点,∴FG是△BEC的中位线,∴FG= BC=2.5,故选B.8.(2023山东东营广饶期末)如图,在▱ABCD中,E,F是对角线 BD上的两点,则添加以下条件不能判定四边形AECF为平行 四边形的是 ( ) A.BE=DF B.AF⊥BD,CE⊥BDC.∠BAE=∠DCF D.AF=CE解析 如图,连接AC,与BD相交于点O, ∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.A.∵BE=DF,∴OB-BE=OD-DF,即OE=OF,∴四边形AECF是 平行四边形;B.∵AF⊥BD,CE⊥BD,∴∠AFD=∠CEB=90°,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADF=∠CBE, ∴△ADF≌△CBE(AAS),∴DF=BE,由A知四边形AECF是平 行四边形;C.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠ ABE=∠CDF,又∵∠BAE=∠DCF,∴△ABE≌△CDF(ASA), ∴BE=DF,由A知四边形AECF是平行四边形;D.由AF=CE不能得到△ADF≌△CBE,无法判定四边形 AECF是平行四边形.故选D.9.(2022辽宁阜新期末)如图,在四边形ABCD中,AB=CD,对角 线AC,BD交于点O,AF⊥BD于点F,CE⊥BD于点E,连接AE, CF.若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形 ABCD是平行四边形;④图中共有4对全等三角形.其中正确的是 ( )A.①③④ B.①②④ C.①②③ D.②③④C 解析 在Rt△DCE和Rt△BAF中, ∴Rt△DCE≌Rt△BAF(HL),∴CE=AF,∵CE⊥BD,AF⊥BD, ∴CE∥AF,∴四边形AECF是平行四边形,∴CF=AE,故①正 确;∵四边形AECF是平行四边形,∴OE=OF,故②正确;∵DE =BF,∴DE-EF=BF-EF,即DF=BE,∴DF+OF=BE+OE,即DO= BO,∵四边形AECF是平行四边形,∴AO=CO,∴四边形ABCD是平行四边形,故③正确;由题意可得△DCF≌△BAE,△CDO≌△ABO,△CDE≌△ABF,△DCB≌△ BAD,△CFO≌△AEO,△CFB≌△AED,△CFE≌△AEF,△ CEO≌△AFO,△ADF≌△CBE,△DOA≌△BOC,△DCA≌ △BAC,△AFC≌△CEA,共12对全等三角形,故④错误.∴正 确的结论是①②③,故选C.10.(手拉手模型)(2022山东济宁任城期末)如图,在△ABC中, AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形, 下列结论:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8,其中错误的个数是 ( ) A.1 B.2 C.3 D.4A解析 ∵AB=3,AC=4,BC=5,32+42=52,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∴AB⊥AC,故①结论正确;∵△ABD,△ACE都是等边三角形,∴∠DAB=∠EAC=60°,∴∠DAE=360°-90°-60°-60°=150°,∵△ABD和△FBC都是等边三角形,∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,∴ ∠DBF=∠ABC,在△ABC和△DBF中, ∴△ABC≌△DBF(SAS),∴AC=DF=4,∵△ACE是等边三角形,∴AE=AC=4,∴DF=AE,同理可证△ABC≌△EFC(SAS),∴AB=EF,∵△ABD是等边三角形,∴AB=AD=3,∴EF=AD,∴四边形AEFD是平行四边形,故②结论正确;∵四边形AEFD是平行四边形,∴∠DFE=∠DAE=150°,故③结论正确;如图,过A作AG⊥DF于G,则∠AGD=90°,∵四边形AEFD是平行四边形,∴AD∥EF,∴∠FDA=180°-∠DFE=180°-150°=30°,∴AG= AD= ,∴S▱AEFD=DF·AG=4× =6,故④结论错误.∴错误结论的个数是1,故选A.二、填空题(每小题3分,共24分)11.(方程思想)(2022山东菏泽中考)若正n边形的一个内角与 一个外角度数的比是3∶2,则n= .5解析 正n边形的各个内角都相等,各个外角也都相等.设一 个外角的度数为2x,则与它相邻的内角的度数为3x,则2x+3x=180°,解得x=36°,∴2x=72°,∵正n边形的外角和为360°,∴n=360°÷72°=5,故答案为5.12.(新考向·开放性试题)(2024黑龙江绥化期末)如图,在四边 形ABCD中,AB∥CD,若添加AD∥BC,则四边形ABCD为平 行四边形.现在请你添加一个适当的条件: ,使得四边形AECF为平行四边形.(图中不再添加点和线)BE=DF(答案不唯一)解析 添加的条件:BE=DF.证明:∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF,又∵BE=DF,∴△ABE≌△CDF(SAS),∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠EFC,∴AE∥FC,∴四边形AECF为平行四边形.故答案为BE=DF.(答案不唯一)13.如图,已知P是▱ABCD的边BC上一点,连接AP,DP,如果 AB=AD=AP,∠B=80°,那么∠CDP的度数为 .30°解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=80°,AD∥BC,∴∠PAD=∠APB,∵AB=AP,∴∠APB=∠B=80°,∴∠PAD=80°,∵AP=AD,∴∠ADP=∠APD=(180°-80°)÷2=50°,∴∠CDP=∠ADC-∠ADP=80°-50°=30°.14.(2023河南商丘永城期末)如图,五边形ABCDE是正五边 形,且l1∥l2.若∠1=57°,则∠2= .129°解析 如图,过点B作BF∥l2交DE于点F, ∵l1∥l2,∴BF∥l1,∵五边形ABCDE是正五边形,∴∠ABC= =108°,∵BF∥l1,∠1=57°,∴∠ABF=∠1=57°,∴∠CBF=∠ABC-∠ABF=108°-57°=51°,∵BF∥l2,∴∠2+∠CBF=180°,∴∠2=180°-51°=129°,故答案为129°.15.(易错题)(2023山东烟台莱州期末)如图,在8×8的正方形网 格中,每个小正方形的顶点称为格点,其中点A,B,C均在格点 上,若点A的坐标为(0,0),点B的坐标为(2,-1),请在给定的网格 中找出格点E,使以A、B、C、E为顶点的四边形是平行四边 形,则点E的坐标为 .(-1,-1)或(1,1)或(5,-1)解析 本题有三种情况.根据题意建立平面直角坐标系,如图所示. 故点E的坐标为(-1,-1)或(1,1)或(5,-1).16.(2023山东威海荣成校级期末)如图,平行四边形ABCD中, AC、BD相交于点O,OE⊥AC交边BC于E,连接AE,若∠ABC =60°,∠BAE=∠DAC,则∠BAE= .40°解析 ∵四边形ABCD是平行四边形,∴AD∥BC,AO=CO,∴∠DAC=∠ACB,∠ABC+∠BAD=180°,∴∠BAD=180°-∠ABC=120°,∵OE⊥AC,∴AE=EC,∴∠CAE=∠ACE,∵∠BAE=∠DAC,∴∠BAE=∠DAC=∠EAC,∴∠BAE=40°.17.小明计算一个多边形的内角和时误把一个外角加进去了, 得其和为2 260°,则这个多边形的边数为 .14解析 设这个多边形的边数为n,多加的一个外角的度数为α, 则(n-2)·180°=2 260°-α,∵内角和是180°的整数倍,0°<α<180°,且2 260°=12×180°+100°,∴小明多加的一个外角的度数为100°,这个多边形的边数为 12+2=14.18.如图,在△ABC中,∠C=90°,D为BC的中点,DE⊥BC,交AB 于点O,BE∥AD,连接AE.以下结论:①四边形ACDE是平行四 边形;②OE=OD;③S四边形ACBE=3S△ACD.其中正确的结论是 .(写出所有正确结论的序号)①②③解析 ∵D为BC的中点,∴BD=CD,∵DE⊥BC,∠C=90°,∴∠BDE=∠C=90°,∴DE∥AC,∵BE∥AD,∴∠EBD=∠ADC,∴△BDE≌△DCA(ASA),∴DE=AC,∴四边形ACDE是平行四边形,故①正确;∵△BDE≌△DCA,∴BE=AD,∵BE∥AD,∴四边形ADBE是平行四边形,∴OE=OD,故②正确;∵四边形ACBE的面积=四边形BDAE的面积+△ACD的面积 =BD·DE+ DC·AC=DC·AC+ DC·AC= DC·AC=3× DC·AC=3S△ACD,∴S四边形ACBE=3S△ACD,故③正确.综上所述,正确的结论 是①②③,故答案为①②③.三、解答题(共46分)19.(2024山东临沂期中)(10分)阅读小明和小红的对话,解决 下列问题. (1)通过列方程说明“多边形的内角和不可能是1 470°”.(2)求该多边形的内角和.(3)若这是一个正多边形,求该正多边形的一个内角比一个外 角大多少.解析 (1)设多边形的边数为n.由题意得(n-2)·180°=1 470°,解得n=10 .∵n为正整数,∴多边形的内角和不可能为1 470°.(2)设这个多边形的边数为n,多加的锐角为α(0°<α<90°),由题 意得(n-2)·180°=1 470°-α,∴
相关资料
更多









