华东师大版七年级数学上册期末素养综合测试(一)课件

这是一份华东师大版七年级数学上册期末素养综合测试(一)课件，共47页。
1.(2023广西中考)若零下2摄氏度记为-2 ℃,则零上2摄氏度 记为 (　    )A.-2 ℃　    B.0 ℃　    C.+2 ℃　    D.+4 ℃
一、选择题(每小题3分,共30分)
解析　由零下2摄氏度记为-2 ℃可知,零下记为“-”,零上记 为“+”,∴零上2摄氏度记为+2 ℃.故选C.
2.(2024广东广州番禺期末)关于单项式- ,下列说法中正确的是 (　    )A.它的次数是3　    B.它的系数是-1C.它的系数是 　    D.它的次数是2
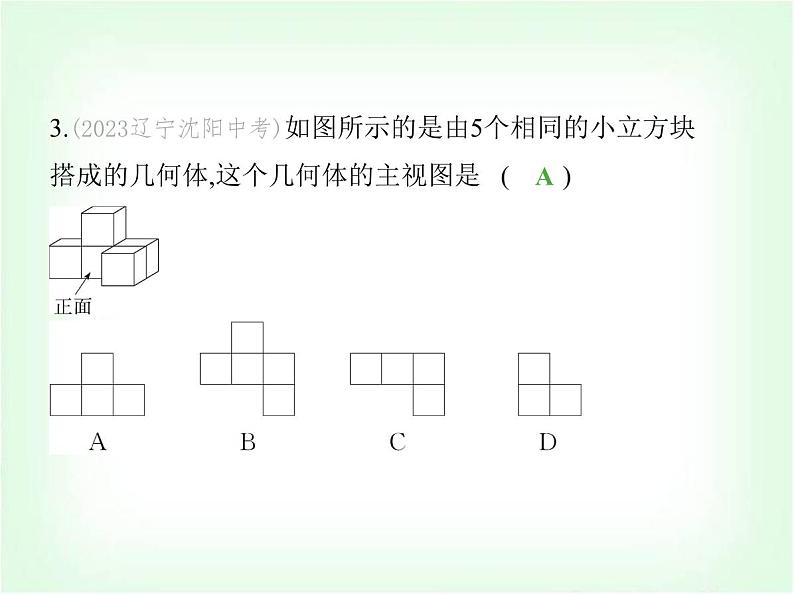
3.(2023辽宁沈阳中考)如图所示的是由5个相同的小立方块 搭成的几何体,这个几何体的主视图是 (　    )  　     　     　     
解析　此几何体的主视图共3列,从左往右小正方形的个数 分别是1,2,1.故选A.
4.(2023海南中考)共享开放机遇,共创美好生活.2023年4月10 日至15日,第三届中国国际消费品博览会在海南省海口市举 行,以“打造全球消费精品展示交易平台”为目标,进场观众 超32万人次,数据320 000用科学记数法表示为(　    )A.3.2×104　    B.3.2×105　    C.3.2×106　    D.32×104
解析    320 000=3.2×105.故选B.
5.(2023湖南衡阳耒阳期末)如图,直线AB、CD相交于点E,EF ⊥AB于E,若∠CEF=54°,则∠BED的度数为 (　    ) A.26°　    B.24°　    C.36°　    D.46°
解析　∵EF⊥AB,∠CEF=54°,∴∠AEC=36°,∵∠BED=∠AEC,∴∠BED=36°.故选C.
6.(2024辽宁葫芦岛龙港期末)如果单项式3xmy2与-5x3yn是同类 项,那么(-m)n的值为 (　    )A.-6　    B.-9　    C.6　    D.9
解析　根据题意可得,m=3,n=2,∴(-m)n=(-3)2=9.故选D.
7.(2023江苏南通中考)如图,△ABC中,∠ACB=90°,顶点A,C分 别在直线m,n上,若m∥n,∠1=50°,则∠2的度数为 (　    ) A.140°　    B.130°　    C.120°　    D.110°
解析　如图, ∵m∥n,∠1=50°,∴∠ACD=∠1=50°,∵∠ACB=90°,∴∠BCD=∠ACB-∠ACD=40°,∴∠2=180°-∠BCD=140°.故选A.
8.如图所示,已知点C是线段AB的中点,点D满足BD= BC,若CD=9 cm,则AB的长为 (　    ) A.32 cm　    B.24 cm　    C.20 cm　    D.15 cm
解析　∵BD= BC,CD=9 cm,∴CD= BC=9(cm),∴BC=12 cm,∵C是线段AB的中点,∴AB=2BC=24(cm).故选B.
9.(新独家原创)新定义运算“@”,规定对于任意的有理 数a、b,a@b=a3-2ab+b,例如,1@2=13-2×1×2+2=-1,则(-2)@(-3)的结果为 (　    )A.-17　    B.-21　    C.-23　    D.23
解析    (-2)@(-3)=(-2)3-2×(-2)×(-3)+(-3)=-8-12-3=-23,故选C.
10.(2023福建莆田涵江第二片期中)如图,AB∥CD,则∠A、 ∠C、∠E、∠F满足的数量关系为 (　    ) A.∠A+∠C+∠F=∠E　    B.∠A+∠C+∠E+∠F=360°C.∠A+∠C+∠E-∠F=180°D.∠A+∠C-∠E+∠F=180°　    
解析　过E作EM∥AB,过F作FN∥AB,∵AB∥CD,∴EM∥FN ∥CD,∴∠A+∠AEM=180°,∠MEF=∠NFE,∠NFC=∠C,∴∠C+∠MEF=∠NFE+∠NFC=∠EFC,∴∠MEF=∠EFC-∠C, ∵∠AEM=∠AEF-∠MEF=∠AEF+∠C-∠EFC,∴∠A+∠C+ ∠AEF-∠EFC=180°.故选C. 
二、填空题(每小题3分,共24分)
11.(2024天津滨海新区期中)计算: - =　　　    . 
12.(2024吉林长春宽城期末)将多项式-3x-4x3+9x2+6按x降幂 排列为　　　　　　    .
-4x3+9x2-3x+6
解析　由题意得-3x-4x3+9x2+6=-4x3+9x2-3x+6.
13.(2024河南洛阳伊川期中)某地一天早晨的气温是-7 ℃,中 午气温上升了9 ℃,下午又下降了11 ℃,晚上又下降了3 ℃,则 晚上的温度为　　　    ℃.
解析　-7+9-11-3=-12(℃).
14.(2024重庆万州期末)如图,已知直线AB与CD相交于点O, EO⊥CD,若∠AOD=148°,则∠BOE的补角的度数为　　        .
解析　∵∠AOD+∠BOD=180°,∠AOD=148°,∴∠BOD=180°-148°=32°,∵EO⊥CD,∴∠BOD+∠BOE=90°,∴∠BOE=90°-32°=58°,∴∠BOE的补角为180°-58°=122°,故答案为122°.
15.(2024重庆綦江期末)已知a2+a-1=0,则代数式4a2+4a+2 024 的值是　　　    .
解析　∵a2+a-1=0,∴a2+a=1,∴4a2+4a+2 024=4(a2+a)+2 024= 4×1+2 024=2 028.
16.(2024甘肃白银市白银区期末)如图,AB∥CD,直线EF分别 交AB、CD于点E、F,EG平分∠AEF,∠1=40°,则∠2的度数 为　　　    .
解析　∵EG平分∠AEF,∴∠AEG=∠GEF,∵AB∥CD,∴∠AEG=∠1=40°,∴∠AEF=2∠AEG=80°,∴∠2=180°-∠AEF=180°-80°=100°.故答案为100°.
17.(新考向·规律探究试题)(2024广东广州白云期末)如图,把 每个正方形等分为4格,在每格中填入数字,各个正方形的四 个数之间都有相同的规律,根据此规律,x=　　　    .(用a,b表 示)      …  
解析　观察可得,9=2×4+1;20=3×6+2;35=4×8+3;……,∴x=18b+a.故答案为18b+a.
18.(2023江苏盐城月考)如图,AB∥CD,则∠1+∠2+∠3+…+ ∠n-1+∠n=　 　　    .
解析　如图1,∵AB∥CD,∴∠1+∠2=180°.如图2,过点E作AB 的平行线,则∠1+∠2+∠3=2×180°.∵两个角有一组互补的 同旁内角,三个角有两组互补的同旁内角,……,∴n个角有(n- 1)组互补的同旁内角,∴∠1+∠2+∠3+…+∠n-1+∠n=180·(n -1).故答案为180°·(n-1). 
三、解答题(共66分)
19.[答案含评分细则](2024四川成都简阳期末)(6分)计算:(1)(-3)-(+7)+2÷ .(2)16÷(-2)3+(0.25-1)×(-4).
解析    (1)原式=-3-7+2×  1分=-3-7-3=-13. 3分(2)原式=16÷(-8)+(-0.75)×(-4) 4分=-2+3=1. 6分
20.[答案含评分细则](8分)(1)(2024四川泸州泸县五中期末)化简:7a+3(a-3b)-2(b-3a).(2)(2024辽宁葫芦岛龙港期末)先化简,后求值:-2(mn-3m2)-[m2 -5(mn-m2)+2mn].其中m=3,n=-4.
解析    (1)原式=7a+3a-9b-2b+6a 2分=16a-11b. 3分(2)原式=-2mn+6m2-(m2-5mn+5m2+2mn)=-2mn+6m2-m2+5mn-5m2-2mn=mn, 6分当m=3,n=-4时,原式=3×(-4)=-12. 8分
21.[答案含评分细则](情境题·现实生活)(2024吉林四平梨树 期末)(8分)某公司6天内货品进出仓库的吨数如下:(“+”表 示进库,“-”表示出库)+31,-32,-16,+35,-38,-20.(1)经过这6天,仓库里的货品　　　    (填“增多了”或“减 少了”).(2)经过这6天,仓库管理员结算发现仓库里还有货品460吨, 那么6天前仓库里有货品多少吨?(3)如果进出的装卸费都是每吨5元,那么这6天要付多少元装 卸费?
解析    (1)+31-32-16+35-38-20=-40(吨),∵-40