初中数学华东师大版（2024）七年级上册（2024）第3章 图形的初步认识3.6 角2. 角的比较和运算背景图课件ppt

这是一份初中数学华东师大版（2024）七年级上册（2024）第3章 图形的初步认识3.6 角2. 角的比较和运算背景图课件ppt，共60页。

知识点1　角的大小比较和画法
1.如图,若∠AOB=∠COD,则∠1与∠2的大小关系是(　    )A.∠1>∠2　    B.∠1=∠2C.∠1<∠2　    D.无法比较
解析　因为∠AOB=∠COD,所以∠AOB-∠BOD=∠COD-∠BOD,所以∠1=∠2.
2.(2024河南信阳罗山期末)已知∠A=30°45',∠B=30.45°,则∠A　　　    ∠B.(填“>”“<”或“=”)
解析　∵∠A=30°45'=30.75°,∠B=30.45°,30.75°>30.45°,∴∠A>∠B.故答案为>.
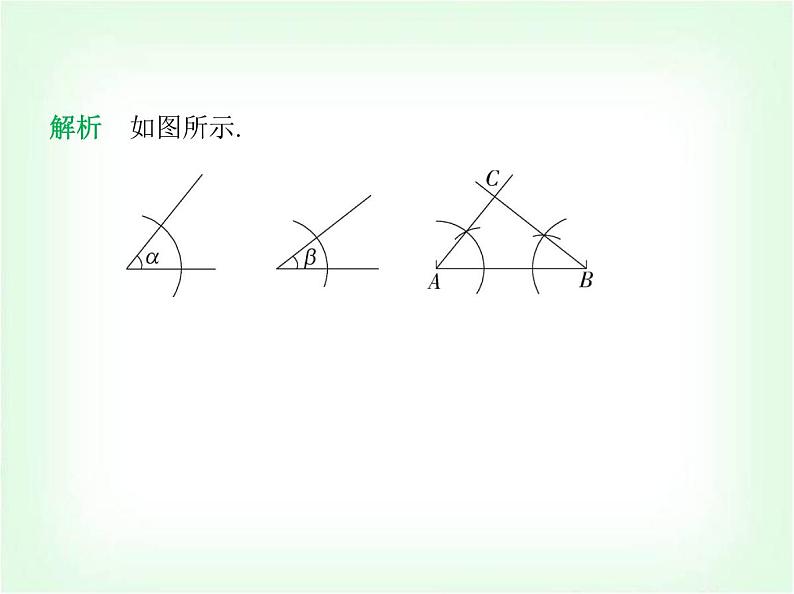
3.(尺规作图)如图所示,已知线段AB,∠α,∠β,分别过A、B作 ∠CAB=∠α,∠CBA=∠β.(不写作法,保留作图痕迹) 
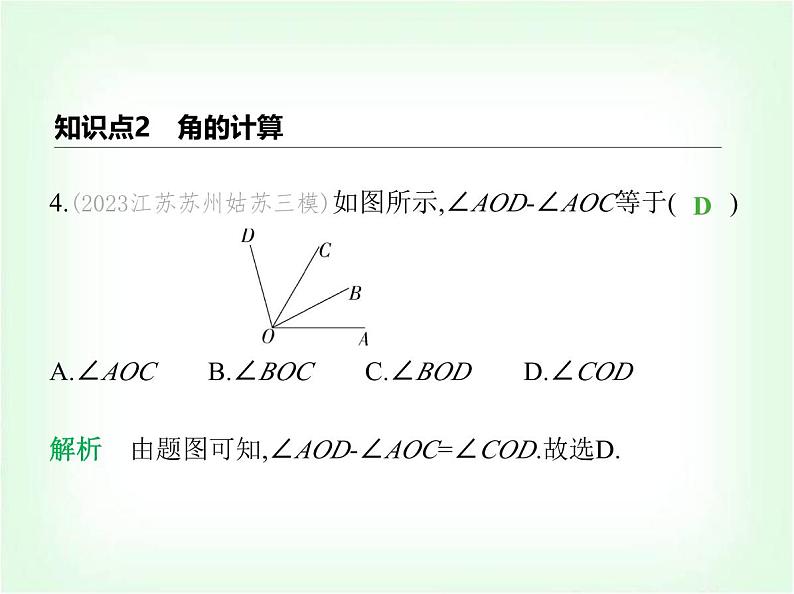
4.(2023江苏苏州姑苏三模)如图所示,∠AOD-∠AOC等于(        ) A.∠AOC　    B.∠BOC　    C.∠BOD　    D.∠COD
解析　由题图可知,∠AOD-∠AOC=∠COD.故选D.
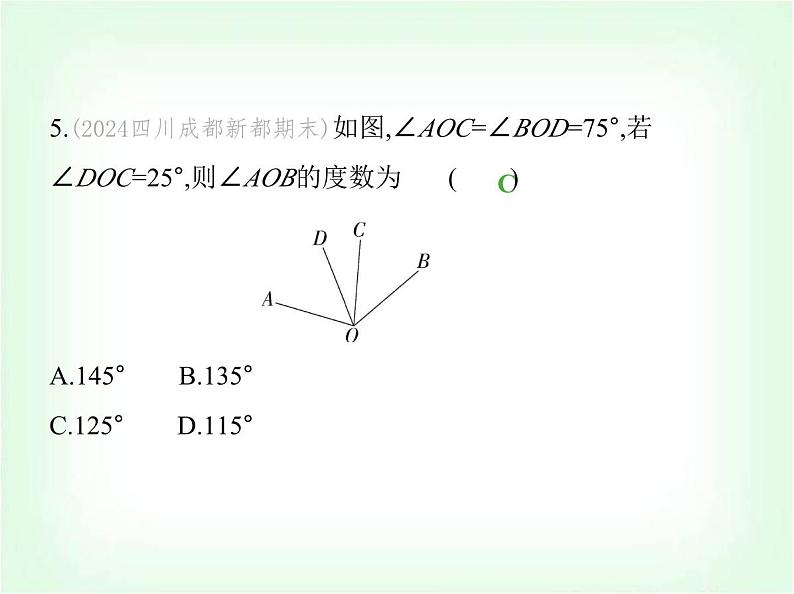
5.(2024四川成都新都期末)如图,∠AOC=∠BOD=75°,若∠DOC=25°,则∠AOB的度数为     (　    ) A.145°　    B.135°　    C.125°　    D.115°
解析　∵∠BOD=75°,∠DOC=25°,∴∠BOC=∠BOD-∠DOC =75°-25°=50°,∴∠AOB=∠AOC+∠BOC=75°+50°=125°.故选C.
6.(2024江苏南京秦淮期末)用一副直角三角板,不能画出的 角的度数是 (　    )A.15°　    B.75°　    C.145°　    D.165°
解析　一副直角三角板的6个角的度数分别为30°,60°,90°,45°,45°,90°,A.∵45°-30°=15°,∴用三角板能够画出15°的角,故此选项不符合题意;B.∵30°+45°=75°,∴用三角板能够画出75°的角,故此选项不符合题意;C.用三角板不能画出145°的角,故此选项符合题意;D.∵90°+45°+30°=165°,∴用三角板能够画出165°的角,故此选项不符合题意.故选C.
7.(2023陕西西安新城爱知中学期末)如图,已知∠AOC=70°, ∠BOD的度数比∠AOC的度数少10°,若∠BOC=20°,则∠AOD的度数等于(　    ) A.130°　    B.110°　    C.115°　    D.150°
解析　∵∠AOC=70°,∠BOD的度数比∠AOC的度数少10°, ∴∠BOD=∠AOC-10°=70°-10°=60°,∵∠BOC=20°,∴∠COD=∠BOD-∠BOC=60°-20°=40°,∴∠AOD=∠AOC+∠COD=70°+40°=110°,故选B.
8.(1)(2024吉林省名校调研期末)计算:11°22'+42°48'=　　        .(2)(2024江苏盐城大丰期末)计算:70°-15°40'=　　　　    .
解析    (1)原式=11°+22'+42°+48'=(11°+42°)+(22'+48')=53°+70'=53°+1°+10'=54°10'.(2)原式=69°60'-15°40'=(69°-15°)+(60'-40')=54°+20'=54°20'.
9.如图,填空. (1)∠AOC=∠AOB+　 　    =∠AOD-　　　    .(2)∠BOC=∠AOC+∠BOD-　　　    .(3)若∠AOC=∠BOD,则∠AOB=　　　    .
解析    (1)由题图易知∠AOC=∠AOB+∠BOC=∠AOD-∠COD.(2)因为∠AOC=∠AOB+∠BOC,∠BOD=∠BOC+∠COD,∠AOD=∠AOB+∠BOC+∠COD,所以∠BOC=∠AOC+∠BOD-∠AOD.(3)因为∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,且 ∠AOC=∠BOD,所以∠AOB=∠COD.
10.(2024安徽六安金寨期末)如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC∶∠BOC=1∶2.(1)求∠AOC的度数.(2)过点O作射线OD,若∠AOD= ∠AOB,求∠COD的度数. 
解析    (1)∵∠AOC∶∠BOC=1∶2,∠AOB=120°,∴∠AOC=  ∠AOB= ×120°=40°.(2)∵∠AOD= ∠AOB,∴∠AOD=60°,当OD在∠AOB内部时,∠COD=∠AOD-∠AOC=20°,当OD在∠AOB外部时,∠COD=∠AOC+∠AOD=100°.故∠COD的度数为20°或100°.
方法解读　角的和、差、倍、分计算的解题方法角的计算是先分析角之间的关系,再列式表示角之间的关系, 进行相关的计算即可求出相关的角.
11.(2023宁夏石嘴山九中期末)如图所示,AD是△ABC的角平 分线,AE是△ABD的角平分线.若∠BAC=80°,则∠EAD的度 数是(　    ) A.20°　    B.30°　    C.45°　    D.60°
解析　∵AD是△ABC的角平分线,∠BAC=80°,∴∠DAC=∠DAB= ∠BAC=40°,∵AE是△ABD的角平分线,∴∠EAD=20°,故选A.
12.(2024甘肃省武威七中期末)如图,∠AOB=68°,OC平分∠AOD且∠COD=15°,则∠BOD的度数为(　    ) A.28°　    B.38°　    C.48°　    D.53°
解析　∵OC平分∠AOD且∠COD=15°,∴∠AOD=2∠COD= 30°,又∵∠AOB=68°,∴∠BOD=∠AOB-∠AOD=38°,故选B.
13.(2024北京东城期末)如图,OA的方向是北偏东15°,OB的方 向是西北方向,若∠AOC=∠AOB,则OC的方向是(　    ) A.北偏东30°　    B.北偏东45°　    C.北偏东60°　    D.北偏东75°
解析　由题意知∠AOB=45°+15°=60°,则∠AOC=∠AOB=60°,故OC与正北方向的夹角是60°+15°=75°,故OC的方向是北偏东75°.故选D.
14.(2023福建福州晋安期末)已知射线OC在∠AOB的内部,下 列4个表述:①∠AOC= ∠AOB,②∠AOC=∠BOC,③∠AOB=2∠BOC,④∠AOC+∠BOC=∠AOB.其中能表示射线OC是∠AOB的平分线的有(　    )A.1个　    B.2个　    C.3个　    D.4个
解析　①∵∠AOC= ∠AOB,∴∠AOB=2∠AOC,∴∠AOC=∠BOC,∴OC是∠AOB的平分线,故正确.②∵∠AOC=∠BOC,∴OC是∠AOB的平分线,故正确;③∵∠AOB=2∠BOC =∠AOC+∠BOC,∴∠AOC=∠BOC,∴OC是∠AOB的平分 线,故正确;④∵∠AOC+∠BOC=∠AOB,∴当∠AOC=30°,∠BOC=40°,∠AOB=70°时,符合上式,但此时OC不是∠AOB的平分线,故错误.故选C.
15.(教材变式·P161T3)(2023吉林长春期末)如图,点A、O、B 在同一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD= 　　     °.
解析　∵点A、O、B在同一条直线上,∴∠COB=180°-∠AOC=180°-50°=130°,∵OD平分∠AOC,∴∠COD= ×50°=25°,∴∠BOD=∠COB+∠COD=130°+25°=155°.
16.(2024内蒙古呼伦贝尔莫旗期末)如图,OB是∠AOC的平分 线,OD是∠COE的平分线,∠AOE=144°,∠COD=25°,求∠AOB和∠BOD的度数. 
解析　∵OD是∠COE的平分线,∠COD=25°,∴∠COE=2∠COD=50°,∵∠AOE=144°,∴∠AOC=∠AOE-∠COE=144°-50°=94°,∵OB是∠AOC的平分线,∴∠BOC=∠AOB= ∠AOC=47°,∴∠BOD=∠COD+∠BOC=25°+47°=72°.
17.(新考法)(2023河北邯郸武安三模,2,★☆☆)将一副三角尺 按如图所示方式放置,量角器中心与点O重合,OA与0°刻度线 重合.如果三角尺的一边OB与90°刻度线重合,那么与边OC重 合的是(　    )A.15°刻度线　    B.30°刻度线C.45°刻度线　    D.75°刻度线　    
解析　本题利用三角尺、量角器构造图形求角的度数,考查 学生的观察能力和应用能力.由题图可知:∠BOP=30°,∠POC=45°,∠BOA=90°,∴∠AOC=∠BOA-∠BOP-∠POC=90°-30°-45°=15°.故选A.
18.(2023广西钦州浦北期末,8,★★☆)如图,已知∠AOB=120°,从∠AOB的内部引两条射线OM,ON,使得∠MON=60°,那么 ∠AON与∠BOM满足的关系是(　    )A.∠AON=∠BOM　    B.∠AON=2∠BOMC.∠AON+∠BOM=120°D.∠AON+∠BOM=180°
解析　∵∠AOB=∠AOM+∠BON+∠MON=120°,∠MON=60°,∴∠AOM+∠BON=60°.∴∠AON+∠BOM=∠AOM+∠MON+∠BON+∠MON=∠AOM+∠BON+2∠MON=60°+2×60°=180°.故选D.
19.(2024广东东莞大朗一中学际联盟期末,10,★★☆)如图, 已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,则 ∠MON的度数是(　    ) A. 　    B. (α-β)　    C.α- 　    D. 
解析　∵∠AOB=α,∠BOC=β,∴∠AOC=α+β,∵OM是∠AOC 的平分线,ON是∠BOC的平分线,∴∠NOC= ∠BOC= ,∠MOC= ∠AOC= ,∴∠MON=∠MOC-∠NOC= - = .故选D.
20.(2023陕西西安新城西光教育集团期中,24,★★☆)如图, 已知∠AOB和三条射线OE、OC、OF在同一个平面内,其中 OE平分∠BOC,OF平分∠AOC.(1)若∠BOC=70°,∠AOC=50°,求∠EOF的度数.(2)若∠BOC=α,∠AOC=β,直接用含α、β的式子表示∠EOF. 
解析    (1)∵OE平分∠BOC,OF平分∠AOC,∴∠COE= ∠BOC,∠COF= ∠AOC,∵∠BOC=70°,∠AOC=50°,∴∠EOF=∠COE+∠COF= ∠BOC+ ∠AOC= ×70°+ ×50°=35°+25°=60°,∴∠EOF的度数为60°.(2)∵∠BOC=α,∠AOC=β,由(1)可知∠EOF=∠COE+∠COF = ∠BOC+ ∠AOC= α+ β= (α+β).
21.(抽象能力)定义:从一个角的顶点出发,把这个角分成1∶2 两个部分的射线,叫做这个角的三分线,一个角的三分线有两 条.如图1,∠AOB=2∠BOC,则OB是∠AOC的一条三分线.(1)如图1,若∠AOC=57°,则∠BOC=　　　    °.
(2)如图2,若∠AOB=120°,OC,OD是∠AOB的两条三分线,且 ∠BOC<∠AOC.①∠COD=　　    °.②若以点O为中心,将∠COD顺时针旋转n°(0解析    (1)∵∠AOB=2∠BOC,∴∠AOC=3∠BOC=57°,∴∠BOC=19°,故答案为19.(2)①∵OC,OD是∠AOB的三分线,且∠BOC<∠AOC,∴∠BOC= ∠AOB=40°,∠AOD= ∠AOB=40°,∴∠COD=∠AOB-∠BOC-∠AOD=40°,故答案为40.②分两种情况:如图1,当OA是∠C'OD'的三分线,且∠AOD'> ∠AOC'时,∠AOC'= ∠C'OD'= ∠COD= °,∴∠DOC'=∠DOA-∠AOC'=40°- °= °,∴∠DOD'=
 °+40°= °;如图2,当OA是∠C'OD'的三分线,且∠AOD'<∠AOC'时,∠AOD'= ∠C'OD'= °,∴∠DOD'=∠DOA+∠AOD'=40°+ °= °. 　     
综上所述,n= 或 .
微专题6　根据角之间的倍、分关系求角的度数
方法指导 根据角的倍、分关系求角的度数的两种思路:(1) 已知基础角的度数,利用这个角的倍、分关系求出相关的角 的度数;(2)已知一个角的倍、分的角的度数,求这个角,通常 是建立方程求解.
1.(2024辽宁营口盖州期末)如图所示,OB是∠AOC的平分线, ∠COD= ∠BOD,∠COD=17°,则∠AOD的度数是 (　    ) A.70°　    B.83°　    C.68°　    D.85°
解析　∵∠COD= ∠BOD,∠COD=17°,∴∠BOC=2∠COD=2×17°=34°,∵OB是∠AOC的平分线,∴∠AOC=2∠BOC=2×34°=68°,∴∠AOD=∠AOC+∠COD=68°+17°=85°,故选D.
2.(2023辽宁大连庄河期末)如图,若O是直线BC上一点,∠AOB=80°,∠COD= ∠AOC,则∠AOD=　　　    .
解析　∵∠AOB+∠AOC=180°,∠AOB=80°,∴∠AOC=100°, ∵∠COD= ∠AOC,且∠AOC=∠COD+∠AOD,∴∠AOD=  ∠AOC= ×100°=80°.故答案为80°.
3.(2023陕西西安未央月考)如图,O是直线AB上的一点,若∠AOC=50°,∠AOD= ∠AOE,∠BOE=90°,则∠DOE的度数是　　　    .