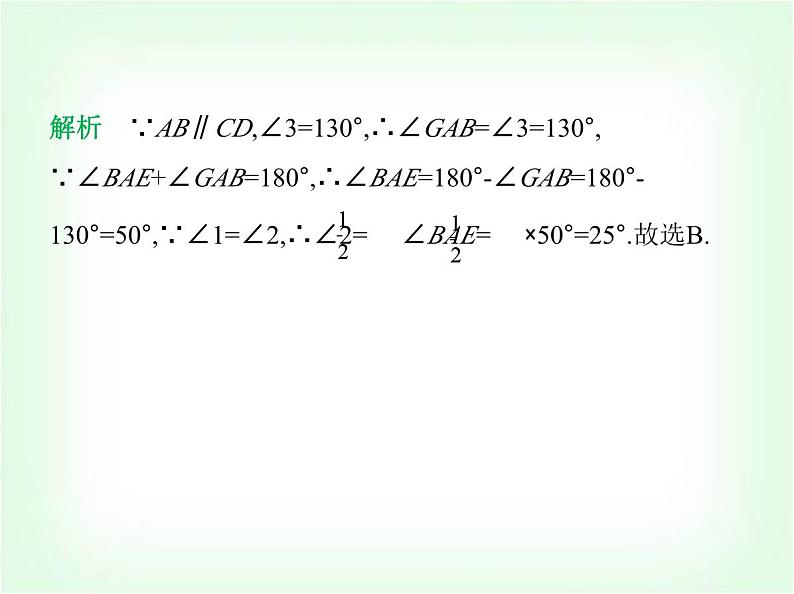
初中华东师大版（2024）3. 平行线的性质课文配套课件ppt

这是一份初中华东师大版（2024）3. 平行线的性质课文配套课件ppt，共9页。

知识点1　两直线平行,同位角相等
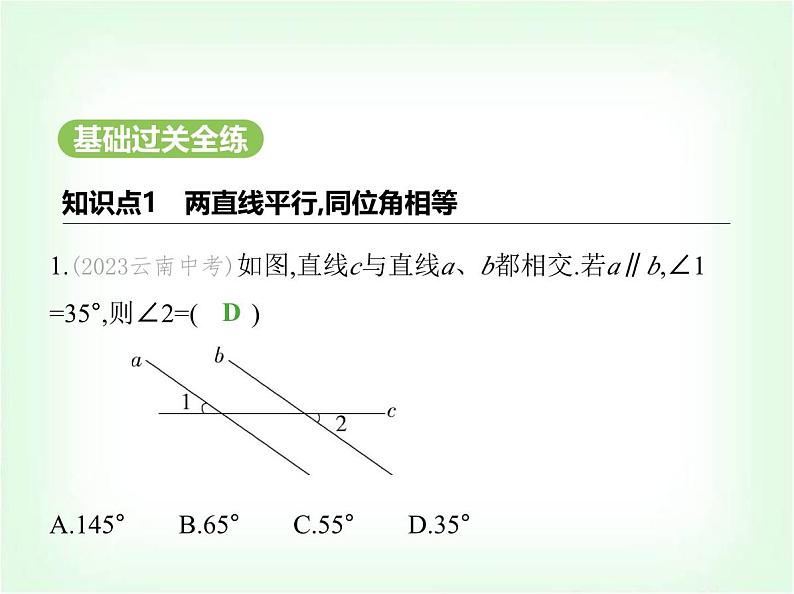
1.(2023云南中考)如图,直线c与直线a、b都相交.若a∥b,∠1 =35°,则∠2=(　    )A.145°　    B.65°　    C.55°　    D.35°
解析　如图, ∵∠1=35°,∴∠3=∠1=35°,∵a∥b,∴∠2=∠3=35°.故选D.
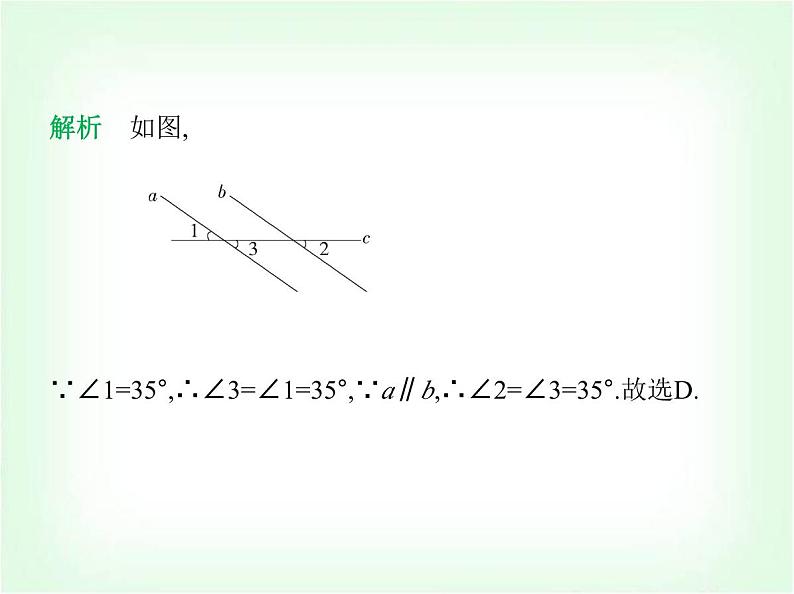
2.(2023河南南阳卧龙期末)如图,a∥b,∠2=120°,则∠1的度数 为(　    ) A.45°　    B.60°　    C.65°　    D.120°
解析　如图,∵∠2+∠3=180°,∠2=120°,∴∠3=60°,∵a∥b, ∴∠1=∠3=60°.故选B. 
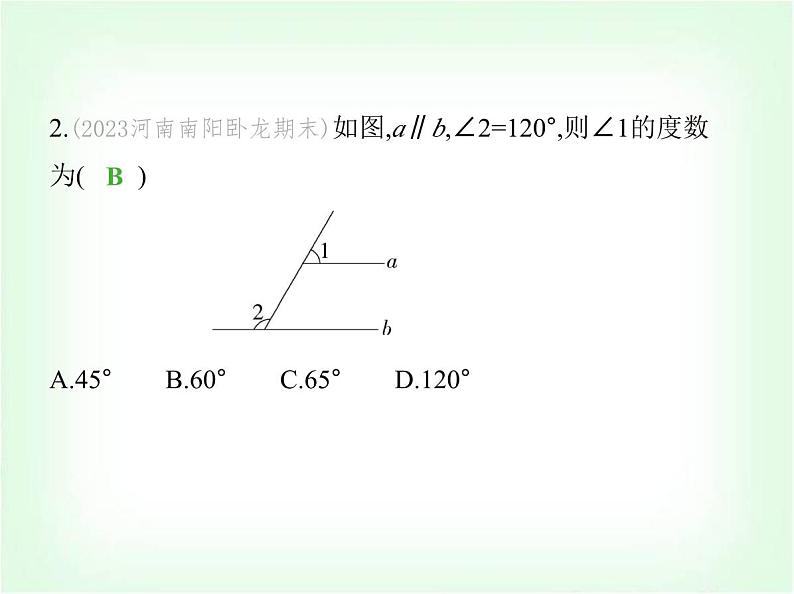
3.(2024四川遂宁期末)如图,AB∥CD,∠1=∠2,∠3=130°,则∠2等于(　    ) A.30°　    B.25°　    C.35°　    D.40°
解析　∵AB∥CD,∠3=130°,∴∠GAB=∠3=130°,∵∠BAE+∠GAB=180°,∴∠BAE=180°-∠GAB=180°-130°=50°,∵∠1=∠2,∴∠2= ∠BAE= ×50°=25°.故选B.
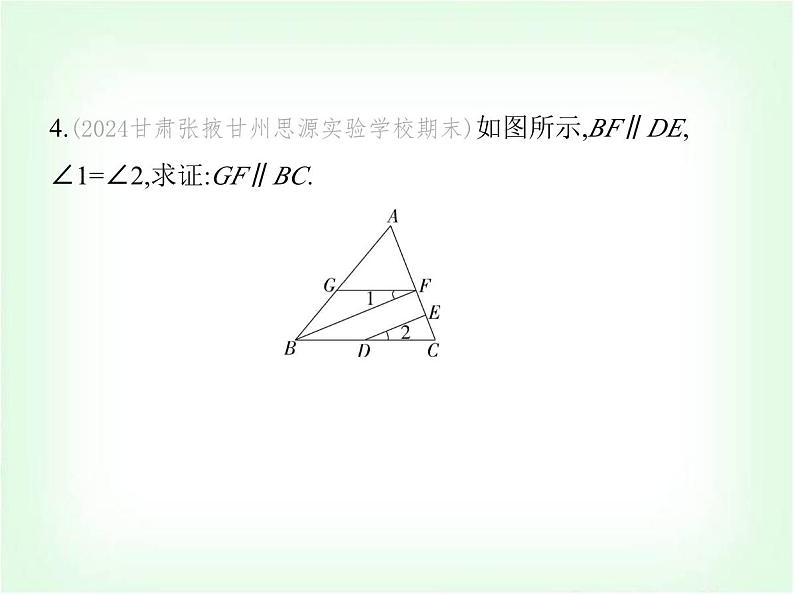
4.(2024甘肃张掖甘州思源实验学校期末)如图所示,BF∥DE, ∠1=∠2,求证:GF∥BC. 
证明　∵BF∥DE,∴∠2=∠FBC(两直线平行,同位角相等), ∵∠2=∠1,∴∠FBC=∠1,∴GF∥BC(内错角相等,两直线平 行).
知识点2　两直线平行,内错角相等
5.(2023重庆中考B卷)如图,直线a,b被直线c所截,若a∥b,∠1= 63°,则∠2的度数为(　    ) A.27°　    B.53°　    C.63°　    D.117°
解析　∵a∥b,∴∠1=∠2,∵∠1=63°,∴∠2=63°.
6.(跨学科·物理)(2023山东烟台中考)一杆古秤在称物时的状 态如图所示,已知∠1=102°,则∠2的度数为　　　    . 
解析　如图,由题意得AB∥CD,∴∠2=∠BCD,∵∠1=102°, ∴∠BCD=78°,∴∠2=78°. 
7.(教材变式·P192T3)(2023湖北黄冈武穴期末)如图,AB∥CD, CE∥GF,若∠1=70°,则∠2=　　　    °.
解析　∵AB∥CD,∴∠1=∠CEF,∵CE∥GF,∴∠2=∠CEF= ∠1=70°.故答案为70.
8.(2024河南洛阳伊川期末)如图,直线EF分别与直线AB,CD 相交于点A,C,AD平分∠BAC,交CD于点D,若∠1=∠2,且∠ADC=54°.(1)直线AB,CD平行吗?为什么?(2)求∠1的度数. 
解析    (1)直线AB,CD平行.理由如下:如图,∵∠2=∠3(对顶角相等),∠1=∠2,∴∠1=∠3,∴AB∥ CD(同位角相等,两直线平行). (2)由(1)知AB∥CD,∴∠DAB=∠ADC=54°,∵AD平分∠BAC,∴∠BAC=2∠DAB=108°, ∴∠2=180°-∠BAC=72°,∴∠1=∠2=72°.
知识点3　两直线平行,同旁内角互补
9.(2023湖北随州中考)如图,直线l1∥l2,直线l与l1,l2相交,若图 中∠1=60°,则∠2=(　    ) A.30°　    B.60°　    C.120°　    D.150°
解析　∵直线l1∥l2,∠1=60°,∴∠2=180°-∠1=180°-60°=120°.故选C.
10.(2024重庆北碚西南大学附中期中)如图,AB∥DE,BC∥ EF,若∠E=118°,则∠B的度数为(　    ) A.62°　    B.72°　    C.102°　    D.118°
解析　如图,∵AB∥DE,∴∠1+∠E=180°,∵∠E=118°,∴∠1 =62°,∵BC∥EF,∴∠B=∠1=62°.故选A. 
11.(2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则 ∠D=　　　    度.
解析　∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,∵BC∥ED, ∴∠D+∠BCD=180°,∴∠D=180°-∠BCD=180°-80°=100°.故答案为100.
12.(2024吉林长春德惠期末)如图,在四边形ABCD中,DE平分 ∠ADC交线段BC于点E,∠1=∠2,∠A=100°.求∠B的度数. 
解析　∵DE平分∠ADC,∠1=∠2,∴∠1=∠2=∠ADE,∴AD∥BC,∴∠A+∠B=180°,∵∠A=100°,∴∠B=80°.
13.(教材变式·P192T4)如图,平移方格纸中的图形,使点A平移 到点A'处,画出平移后的图形. 
解析　平移后的图形如图所示. 
14.(2023山东济南中考,3,★☆☆)如图,一块直角三角板的直 角顶点放在直尺的一边上.如果∠1=70°,那么∠2的度数是 (　    ) A.20°　    B.25°　     C.30°　    D.45°
解析　如图, ∵a∥b,∴∠1=∠3=70°,∴∠2=180°-90°-70°=20°,故选A.
15.(2024辽宁沈阳法库期末,8,★★☆)将一直角三角板与两 边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的个数是 (　    ) A.1　    B.2　    C.3　    D.4
解析　∵纸条的两边互相平行,∴∠1=∠2,∠3=∠4,∠4+∠5=180°,故①②④正确;∵题图中三角形是直角三角形,∴∠2+∠4=180°-90°=90°,故③正确.综上所述,正确的个数是4.故选D.
16.(2024甘肃酒泉玉门五校期末,10,★★☆)如图,AB∥CD∥ EF,则下列各式中正确的是(　    ) A.∠1=180°-∠3　   B.∠1=∠3-∠2C.∠2+∠3=180°-∠1　   D.∠2+∠3=180°+∠1 
解析　∵AB∥CD,∴∠2+∠BDC=180°,即∠BDC=180°-∠2, ∵EF∥CD,∴∠BDC+∠1=∠3,即∠BDC=∠3-∠1,∴180°-∠2=∠3-∠1,即∠2+∠3=180°+∠1,故选D.
17.(2023河北邯郸永年期中,19,★★☆)如图,直线AB∥CD,∠1=∠3,∠C=50°,∠2=25°,则∠BED=　　　    °.
解析　∵∠1=∠3,∴AB∥EF,∵AB∥CD,∴EF∥CD,∴∠3=∠C=50°,∠FED=∠2=25°,∴∠BED=∠3+∠FED=50°+25°=75°.故答案为75.
18.(2024山东济南章丘期末,19,★★☆)如图所示,点B,E分别 在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A =∠F. 
证明　∵∠2=∠3,∠1=∠2,∴∠1=∠3,∴BD∥CE,∴∠C=∠ABD.又∵∠C=∠D,∴∠D=∠ABD,∴AB∥EF,∴∠A=∠F.
19.(2024河南新乡原阳贾村实验学校期末,20,★★☆)如图, 已知AB∥CD,BE平分∠ABC,BE垂直于CE,求证:CE平分∠BCD. 
证明　如图,过E作EF∥AB交BC于点F, 则∠ABE=∠FEB,∵AB∥CD,∴EF∥CD,∠ABC+∠BCD=180°,∴∠DCE=∠FEC,∵BE⊥CE,∴∠BEF+∠CEF=∠ABE+∠DCE=90°,∴∠EBC +∠ECB=90°,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠DCE= ∠BCE,∴CE平分∠BCD.
20.(2023重庆凤鸣山中学期末,22,★★☆)如图,DE⊥AC,∠AGF=∠ABC,∠1=35°,∠2=145°.(1)试判断BF与AC的位置关系,并说明理由.(2)若BF平分∠ABC,求∠A的度数.