华东师大版七年级数学上册专项素养综合练(八)平行线拐点的四种模型练模型课件

这是一份华东师大版七年级数学上册专项素养综合练(八)平行线拐点的四种模型练模型课件，共31页。

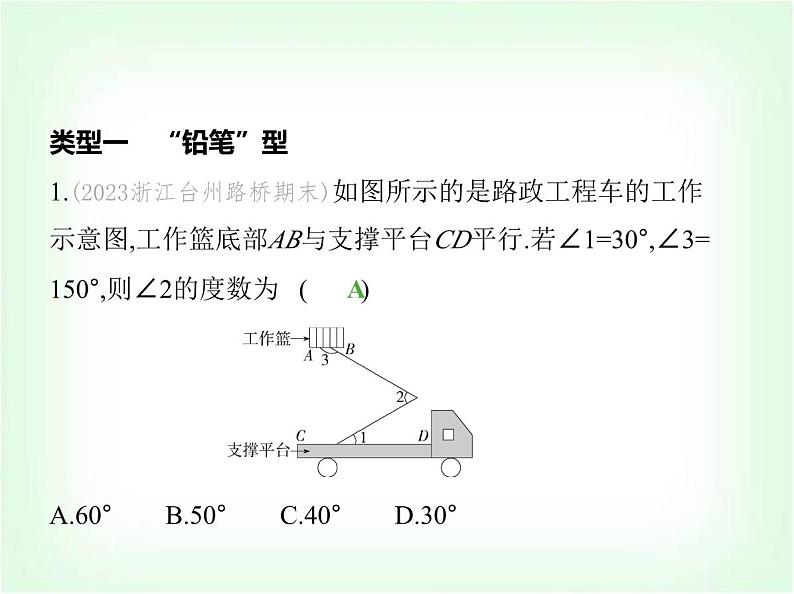
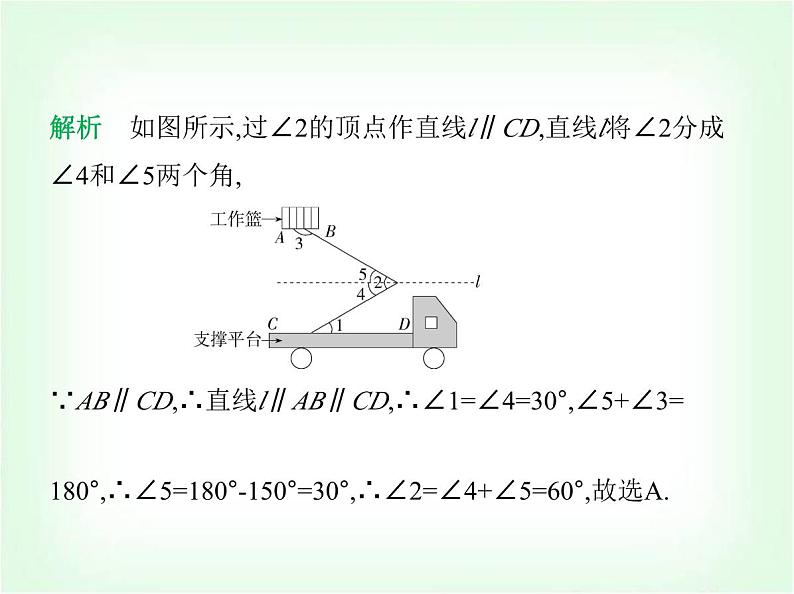
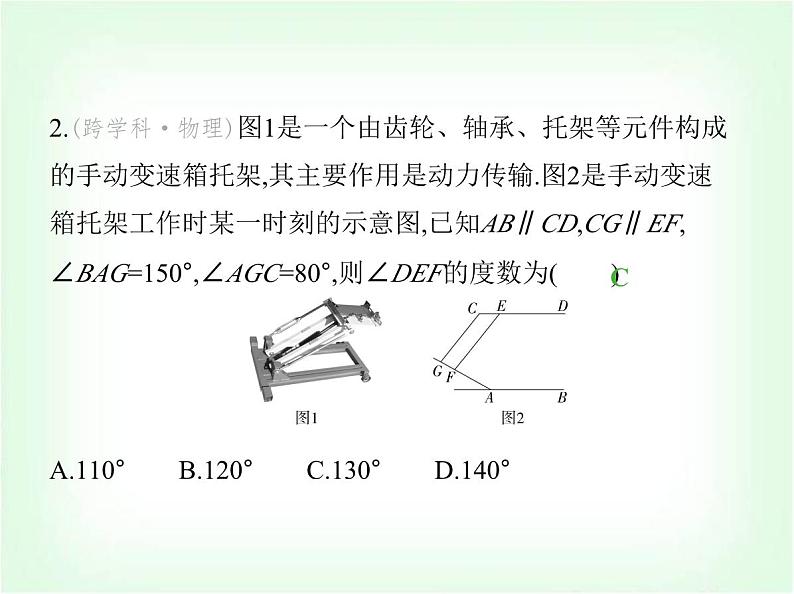
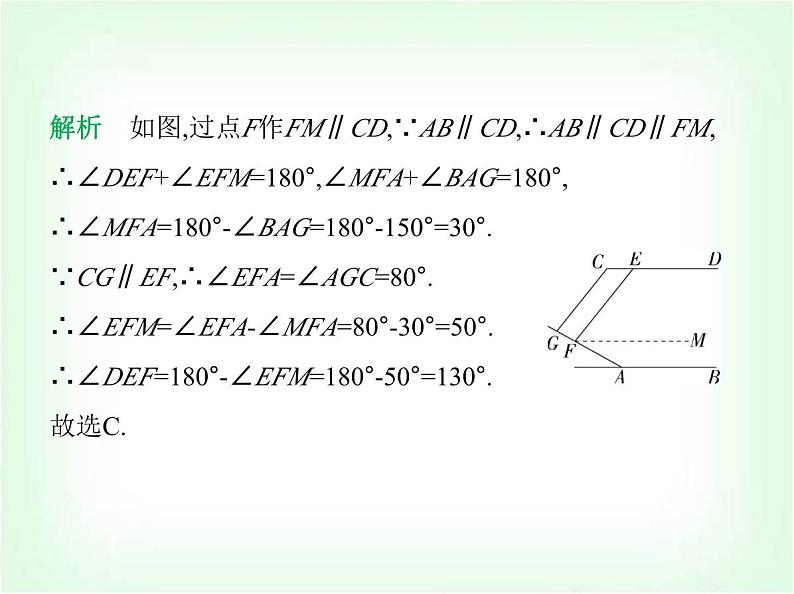
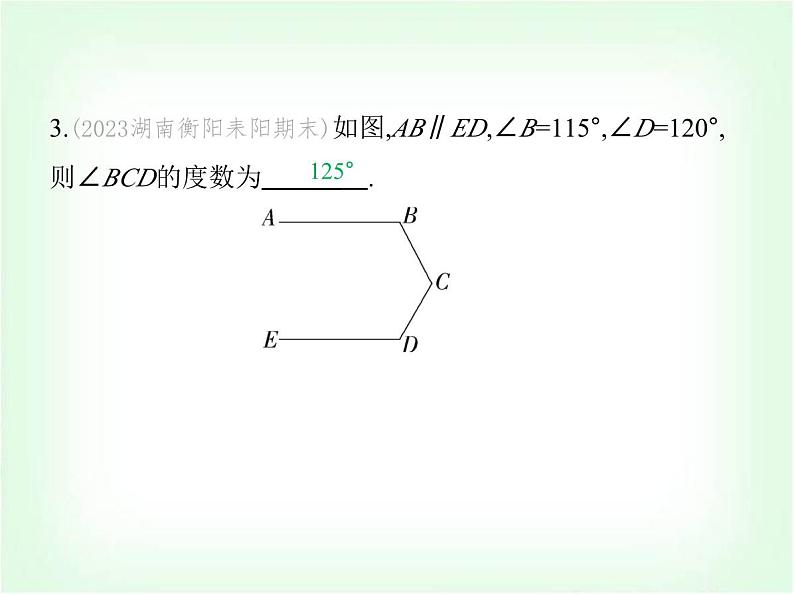
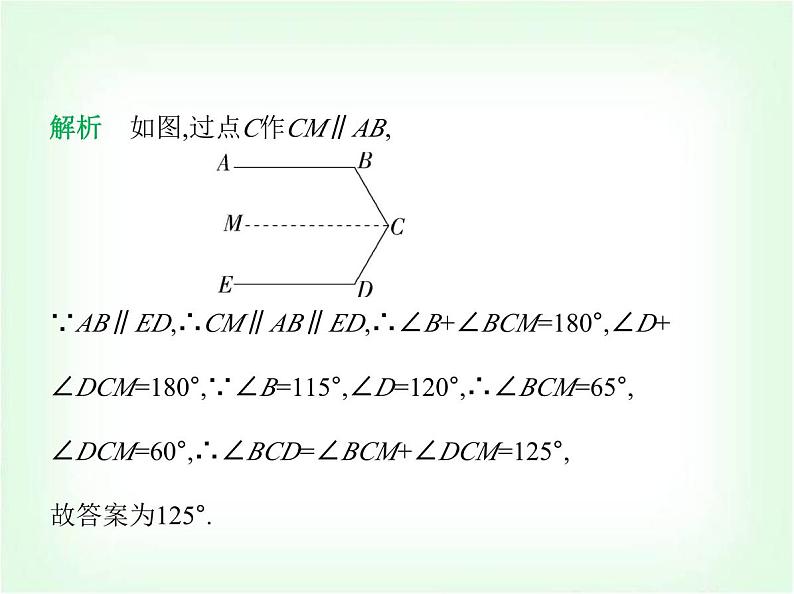
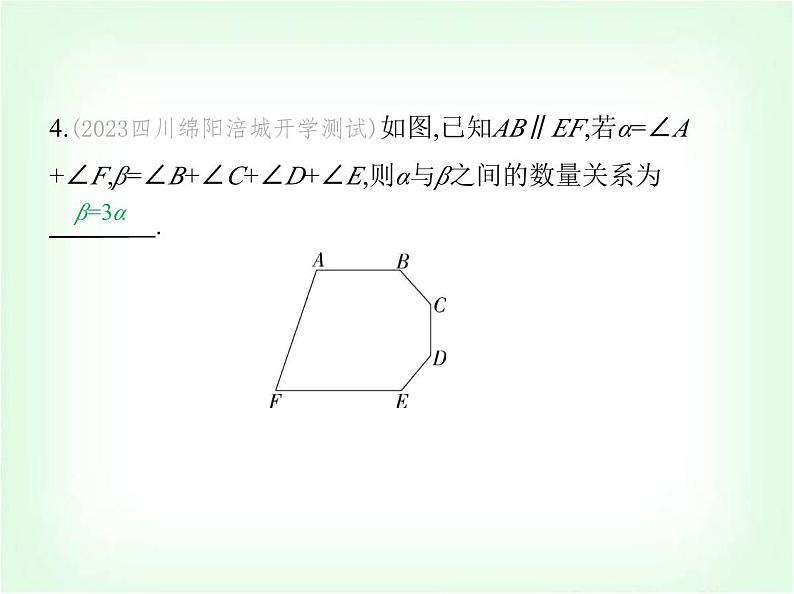
专项素养综合全练(八)　　　　平行线拐点的四种模型　练模型1.(2023浙江台州路桥期末)如图所示的是路政工程车的工作示意图,工作篮底部AB与支撑平台CD平行.若∠1=30°,∠3=150°,则∠2的度数为 (　    ) A类型一　“铅笔”型A.60°　    B.50°　    C.40°　    D.30°解析　如图所示,过∠2的顶点作直线l∥CD,直线l将∠2分成∠4和∠5两个角,∵AB∥CD,∴直线l∥AB∥CD,∴∠1=∠4=30°,∠5+∠3=180°,∴∠5=180°-150°=30°,∴∠2=∠4+∠5=60°,故选A. 2.(跨学科·物理)图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架,其主要作用是动力传输.图2是手动变速箱托架工作时某一时刻的示意图,已知AB∥CD,CG∥EF,∠BAG=150°,∠AGC=80°,则∠DEF的度数为(　    ) CA.110°　    B.120°　    C.130°　    D.140°解析　如图,过点F作FM∥CD,∵AB∥CD,∴AB∥CD∥FM,∴∠DEF+∠EFM=180°,∠MFA+∠BAG=180°,∴∠MFA=180°-∠BAG=180°-150°=30°.∵CG∥EF,∴∠EFA=∠AGC=80°.∴∠EFM=∠EFA-∠MFA=80°-30°=50°.∴∠DEF=180°-∠EFM=180°-50°=130°.故选C.3.(2023湖南衡阳耒阳期末)如图,AB∥ED,∠B=115°,∠D=120°,则∠BCD的度数为　　　    .125°解析　如图,过点C作CM∥AB, ∵AB∥ED,∴CM∥AB∥ED,∴∠B+∠BCM=180°,∠D+∠DCM=180°,∵∠B=115°,∠D=120°,∴∠BCM=65°,∠DCM=60°,∴∠BCD=∠BCM+∠DCM=125°,故答案为125°.4.(2023四川绵阳涪城开学测试)如图,已知AB∥EF,若α=∠A+∠F,β=∠B+∠C+∠D+∠E,则α与β之间的数量关系为　    　    .β=3α解析　如图,过C作CM∥AB,过D作DN∥AB,∵AB∥EF,∴AB∥CM∥DN∥FE,∴∠A+∠F=180°,∠B+∠MCB=180°,∠MCD+∠NDC=180°,∠EDN+∠DEF=180°,∴∠B+∠MCB+∠MCD+∠NDC+∠EDN+∠DEF=180°×3,∴∠B+∠BCD+∠CDE+∠E=180°×3,∵α=∠A+∠F,β=∠B+∠BCD+∠CDE+∠E,∴β=3α.故答案为β=3α.  类型二　“猪蹄”型5.(2023山东济宁邹城一模)如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于 (　    ) A.138°　    B.136°　    C.134°　    D.132°C解析　如图,过点E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD, ∴∠1=∠AEF,∠C+∠FEC=180°,∴∠FEC=180°-44°=136°,∴∠AEF=360°-90°-136°=134°,∴∠1=134°.故选C.6.(2024湖南衡阳耒阳正源学校期末)如图,AB∥CD,则下列关于∠1、∠2、∠3的关系一定成立的是 (　    ) A.∠1+∠2+∠3=180°　    B.∠1+∠2+∠3=360°C.∠1+∠3=2∠2　    D.∠1+∠3=∠2D解析　如图,过点E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD,∴∠AEF=∠1,∠CEF=∠3,∴∠2=∠AEF+∠CEF=∠1+∠3.故选D.  7.(新独家原创)如图,AB∥EF,∠C=90°,∠D=90°,则下列关系式正确的是 (　    ) A.∠α=∠β　     B.∠α+∠β=90°C.∠α+∠β=45°　    D.∠α+∠β=60°A解析　如图,延长BC交EF于H,因为∠BCD=90°,∠D=90°,所以∠BCD=∠D,所以BH∥DE,所以∠β=∠BHE,因为AB∥EF,所以∠α=∠BHE,所以∠α=∠β.故选A.  8.(2024辽宁朝阳建平期末)如图,直线CE∥DF,∠CAB=135°,∠ABD=85°,则∠1+∠2=(　    ) A.30°　    B.35°　    C.36°　    D.40°D解析　如图,过点A作l1的平行线AM,过点B作l2的平行线BN,则∠3=∠1,∠4=∠2,∵l1∥l2,∴AM∥BN,∴∠MAB+∠ABN=180°,∵∠CAB=135°,∠ABD=85°,∴∠3+∠4=135°+85°-180°=40°,∴∠1+∠2=40°.故选D.  9.如图,a∥b,求图中∠BAC,∠ABD,∠1,∠2之间的数量关系.  解析　如图,过点B作BM∥a,过点A作AN∥b,则∠1=∠MBD,∠2=∠CAN,∵a∥b,∴BM∥AN,∴∠ABM=∠BAN,∴∠ABD-∠MBD=∠CAB-∠CAN,即∠ABD-∠1=∠CAB-∠2.  类型三　“飞燕”型10.(2024吉林长春绿园期末)如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是 (　    )A.∠α+∠β-∠γ=90°　    B.∠α+∠γ-∠β=180°C.∠γ+∠β-∠α=180°　    BD.∠α+∠β+∠γ=180°解析　∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠γ+∠α-∠β=180°,故选B.11.(2024辽宁阜新太平期末)如图,已知AB∥CD,∠B=100°,∠E=40°,则∠C=　　　    度.120解析　如图,过E作EF∥AB, ∵AB∥CD,∴AB∥CD∥EF,∴∠B=∠BEF,∠C+∠CEF=180°,∵∠ABE=100°,∴∠BEF=100°,∵∠BEC=40°,∴∠CEF=∠BEF-∠BEC=100°-40°=60°,∴∠C=180°-∠CEF=120°,故答案为120.12.(2022浙江宁波海曙兴宁中学期中)如图,AB∥EG,CD∥EF,BC∥DE,若x=50°,y=30°,求z.  解析    解析　如图所示,延长AB交DE于H, ∵BC∥DE,∴∠ABC=∠AHE=x,∵CD∥EF,∴∠D=∠DEF=z,∴∠DEG=z+y,∵AH∥EG,∴∠AHE=∠DEG=z+y,即x=z+y,∴z=x-y=50°-30°=20°.类型四　“鹰嘴”型13.(跨学科·体育与健康)(2024湖南衡阳期末)乐乐观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC的度数是 (　    )      A.30°　    B.29°　    C.28°　    D.27°B解析　如图,过E作EF∥CD,∵AB∥CD,∴EF∥AB,∵∠BAE=92°,∴∠AEF=180°-92°=88°,又∵∠DCE=121°,∴∠FEC=180°-∠DCE=180°-121°=59°.∴∠AEC=∠AEF-∠FEC=88°-59°=29°.故选B.  14.(2024黑龙江哈尔滨南岗萧红中学期中)如图,AB∥CD,∠A=25°,∠CDP=140°,则∠P=　　　    .65°解析　如图,过P作PM∥AB,∵AB∥CD,∴PM∥CD∥AB,∴∠APM=∠A=25°,∠MPD+∠CDP=180°,∵∠CDP=140°,∴∠MPD=40°,∴∠APD=∠APM+∠MPD=25°+40°=65°.故答案为65°.  15.如图,若AB∥CD,求∠1+∠3-∠2的度数.  解析　如图,过E作EF∥AB,∵AB∥CD,∴EF∥CD,∴∠2+∠FEA=∠3,∴∠FEA=∠3-∠2,∵∠1+∠FEA=180°,∴∠1+∠3-∠2=180°.