2024-2025学年江苏省常州市新北区数学九年级第一学期开学监测试题【含答案】

这是一份2024-2025学年江苏省常州市新北区数学九年级第一学期开学监测试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）将一张多边形纸片沿图中虚线剪开,如果剪开后得到的两个图形的内角和相等,下列四种剪法中符合要求的是( )
A．B．C．D．
2、（4分）为了了解中学课堂教学质量，我市教体局去年对全市中学教学质量进行调查方法是通过考试参加考试的为全市八年级学生，从中随机抽取600名学生的英语成绩进行分析对于这次调查，以下说法不正确的是( )
A．调查方法是抽样调查B．全市八年级学生是总体
C．参加考试的每个学生的英语成绩是个体D．被抽到的600名学生的英语成绩是样本
3、（4分）下列各式-3x，，，-，，，中，分式的个数为（ ）
A．1B．2C．3D．4
4、（4分）如图：，，，若，则等于（ ）
A．B．C．D．
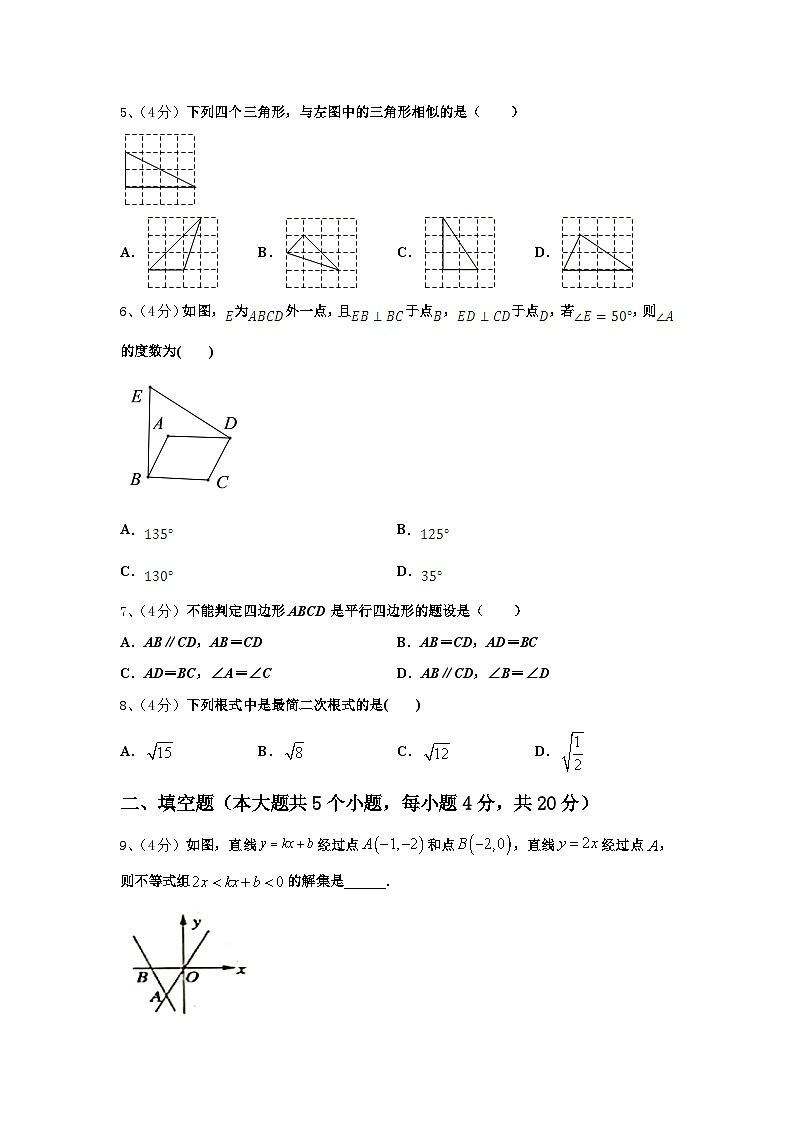
5、（4分）下列四个三角形，与左图中的三角形相似的是（ ）
A．B．C．D．
6、（4分）如图，为外一点，且于点，于点，若，则的度数为( )
A．B．
C．D．
7、（4分）不能判定四边形ABCD是平行四边形的题设是（ ）
A．AB∥CD，AB＝CDB．AB＝CD，AD＝BC
C．AD＝BC，∠A＝∠CD．AB∥CD，∠B＝∠D
8、（4分）下列根式中是最简二次根式的是( )
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，直线经过点和点，直线经过点，则不等式组的解集是______.
10、（4分）在△ABC中，AC＝BC＝，AB＝2，则△ABC中的最小角是_____．
11、（4分）正方形网格中，∠AOB如图放置，则tan∠AOB=______________．
12、（4分）如图，正方形ABCD的面积为，则图中阴影部分的面积为______________ ．
13、（4分）一个样本为1,3，a，b，c，2，2已知这个样本的众数为3，平均数为2，那么这个样本的中位数为_______
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，已知直线l1:y=-2x+4与x、y轴分别交于点N、C，与直线l2:y=kx+b(k≠0)交于点M，点M的横坐标为1，直线l2与x轴的交点为A(-2，0)
（1）求k，b的值;
（2）求四边形MNOB的面积.
15、（8分）在平面直角坐标系xOy中，已知一次函数的图象与x轴交于点，与轴交于点．
（1）求，两点的坐标；
（2）在给定的坐标系中画出该函数的图象；
（3）点M（1，y1），N（3，y2）在该函数的图象上，比较y1与y2的大小.
16、（8分）1号探测气球从海拔5m处出发，以1m/min的速度上升.与此同时，2号探测气球从海拔15m处出发，以0.5m/min的速度上升.两个气球都匀速上升了50min.设气球上升时间为x(x≥0).
(Ⅰ)根据题意，填写下表
(Ⅱ)在某时刻两个气球能否位于同一高度？如果能，这时气球上升了多长时间？位于什么高度？如果不能，请说明理由.
(Ⅲ)当0≤x≤50时，两个气球所在位置的海拔最多相差多少米？
17、（10分）如图，平行四边形中，对角线与相交于点，点为的中点，连接，的延长线交的延长线于点，连接.
（1）求证：；
（2）若，∠BCD=120°判断四边形的形状，并证明你的结论.
18、（10分）某校八年级一班20名女生某次体育测试的成绩统计如下：
(1)如果这20名女生体育成绩的平均分数是82分，求x、y的值；
(2)在(1)的条件下，设20名学生测试成绩的众数是a，中位数是b，求的值.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）在直角坐标系中，点P（﹣2，3）到原点的距离是 ．
20、（4分）设m，n分别为一元二次方程x2+2x﹣1＝0的两个实数根，则m+n+mn＝_____．
21、（4分）如图，在中，，垂足为，是中线，将沿直线BD翻折后，点C落在点E，那么AE为_________.
22、（4分）一个纳米粒子的直径是0.000 000 035米，用科学记数法表示为______米.
23、（4分）函数y＝的自变量x的取值范围为____________．
二、解答题（本大题共3个小题，共30分）
24、（8分）古运河是扬州的母亲河，为打造古运河风光带，现有一段长为180米的河道整治任务由两工程队先后接力完成．工作队每天整治12米，工程队每天整治8米，共用时20天．
（1）根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
甲： 乙：
根据甲、乙两名同学所列的方程组，请你分别指出未知数表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：
甲：x表示________________，y表示_______________；
乙：x表示________________，y表示_______________．
（2）求两工程队分别整治河道多少米．（写出完整的解答过程）
25、（10分）求知中学有一块四边形的空地ABCD，如下图所示，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要250元，问学校需要投入多少资金买草皮？
26、（12分）已知四边形ABCD是矩形，对角线AC和BD相交于点P，若在矩形的上方作△DEA，且使DE∥AC，AE∥BD．
（1）求证：四边形DEAP是菱形；
（2）若AE＝CD，求∠DPC的度数．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据多边形的内角和定理即可判断.
【详解】
A. 剪开后的两个图形一个是三角形、一个是四边形,它们的内角和分别是180°、360°，故此选项不合题意；
B. 剪开后的两个图形一个是三角形、一个是四边形,它们的内角和分别是180°、360°，故此选项不合题意；
C. 剪开后的两个图形都是四边形,它们的内角和都是360°；故此选项符合题意；
D. 剪开后的两个图形一个是三角形、一个是四边形,它们的内角和分别是180°、360°，故此选项不合题意；
故选：C.
此题考查多边形的内角和定理，解题关键在于根据剪开后得到的两个图形来判断.
2、B
【解析】
根据全面调查与抽样调查的定义，总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，对各选项分析后利用排除法求解.
【详解】
、调查方法是抽样调查，正确；
、全市八年级学生的英语成绩是总体，错误；
、参加考试的每个学生的英语成绩是个体，正确；
、被抽到的600名学生的英语成绩是样本，正确.
故选：.
此题考查了总体、个体、样本、样本容量．解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象.总体、个体与样本的考察对象是相同的，所不同的是范围的大小，样本容量是样本中包含的个体的数目，不能带单位.
3、D
【解析】
根据分母中是否含有未知数解答，如果分母含有未知数是分式，如果分母不含未知数则不是分式．
【详解】
-3x，，-的分母中均不含未知数，因此它们是整式，不是分式，
，，，分母中含有未知数，因此是分式，
∴分式共有4个，
故选D.
本题考查的是分式的定义，在解答此题时要注意分式是形式定义，只要是分母中含有未知数的式子即为分式．
4、C
【解析】
过点D作DG⊥AC于点G，先根据∠DAE=∠DAF=15°，DE∥AB，DF⊥AB得出∠ADE=∠DAE=15°，DF=DG，再由AE=6可得出DE=6，根据三角形外角的性质可得出∠DEG的度数，由直角三角形的性质得出DG的长，进而可得出结论．
【详解】
解：过点作于点，
，，
，
．
，
．
是的外角，
，
．
故选C．
本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
5、B
【解析】
设单位正方形的边长为1，求出各边的长，再根据各选项的边长是否成比例关系即可判断.
【详解】
设单位正方形的边长为1，给出的三角形三边长分别为2，4，2．
A、三角形三边分别是2，，3，与给出的三角形的各边不成比例，故A选项错误；
B、三角形三边，2，，与给出的三角形的各边成比例，故B选项正确；
C、三角形三边2，3，，与给出的三角形的各边不成比例，故C选项错误；
D、三角形三边，，4，与给出的三角形的各边不成正比例，故D选项错误．
故选：B．
本题主要应用两三角形相似的判定定理，三边对应成比例，做题即可．
6、C
【解析】
首先由四边形内角和定理求出∠C=130°，然后根据平行四边形对角相等可得答案.
【详解】
解：∵EB⊥BC，ED⊥CD，，
∴∠EBC＝90°，∠EDC＝90°，
∴在四边形EBCD中，∠C=360°-∠EBC-∠EDC-∠E=360°-90°-90°-50°=130°，
∴在中=∠C=130°，
故选：C.
本题考查了四边形的内角和定理，平行四边形的性质，熟练掌握相关性质定理是解题关键．
7、C
【解析】
根据平行四边形的判定，A、B、D均能判断是平行四边形，唯有C不能判定．
【详解】
因为平行四边形的判定方法有：两组对边分别相等的四边形是平行四边形，故B正确；
一组对边平行且相等的四边形是平行四边形，故A正确；
由AB∥CD，∠B＝∠D，可求得∠A＝∠C，根据两组对角分别相等的四边形是平行四边形可以判定，故D也可以判定．
连接BD，利用“SSA”不能判断△ABD与△CDB，C不能判定四边形ABCD是平行四边形，
故选C．
此题主要考查学生对平行四边形的判定的掌握情况．平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．
8、A
【解析】
根据最简二次根式的定义即可求出答案．
【详解】
B.原式，故B不是最简二次根式；
C.原式，故C不是最简二次根式；
D.原式，故D不是最简二次根式；
故选A．
本题考查最简二次根式，解题的关键是正确理解最简二次根式的定义，本题属于基础题型．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
解不等式2x＜kx+b＜0的解集，就是指函数图象在A，B之间的部分的自变量的取值范围．
【详解】
解：根据题意得到y=kx+b与y=2x交点为A（-1，-2），
解不等式2x＜kx+b＜0的解集，就是指函数图象在A，B之间的部分，
又B（-2，0），
此时自变量x的取值范围，是-2＜x＜-1．
即不等式2x＜kx+b＜0的解集为：-2＜x＜-1．
故答案为：-2＜x＜-1．
本题主要考查一次函数与一元一次方程及一元一次不等式之间的内在联系．根据函数图象即可得到不等式的解集．
10、45°．
【解析】
根据勾股定理得到逆定理得到△ABC是等腰直角三角形，根据等腰直角三角形的性质即可的结论.
【详解】
解：∵AC＝BC＝，AB＝2，
∴AC2+BC2＝2+2＝4＝22＝AB2，
∴△ABC是等腰直角三角形，
∴△ABC中的最小角是45°；
故答案为：45°．
本题考查了等腰直角三角形，勾股定理的逆定理，熟练掌握勾股定理的逆定理是解题的关键.
11、1
【解析】
试题解析：如图，
tan∠AOB==1，
故答案为1．
12、
【解析】
试题分析：根据正方形的对称性，可知阴影部分的面积为正方形面积的一半，因此可知阴影部分的面积为.
13、2
【解析】分析：先根据众数为3，平均数为2求出a，b，c的值，然后根据中位数的求法求解即可.
详解：∵这个样本的众数为3，
∴a，b，c中至少有两个数是3.
∵平均数为2，
∴1+3+a+b+c+2+2=2×7，
∴a+b+c=6,
∴a，b，c中有2个3,1个0，
∴从小到大可排列为：0,1,2,2,3,3,3，
∴中位数是2.
故答案为：2.
点睛：本题考查了众数、平均数、中位数的计算，熟练掌握众数、平均数、中位数的计算方法是解答本题的关键.众数是一组数据中出现次数最多的数，众数可能没有，可能有1个，也可能有多个.
三、解答题（本大题共5个小题，共48分）
14、（1）k= ，b= ；（2）
【解析】
（1）根据待定系数法可求出解析式，得到k、b的值;
（2）根据函数解析式与坐标轴的交点，可利用面积公式求出四边形的面积.
【详解】
（1）M为l1与l2的交点
令M(1，y)，代入y=2x+4中，解得y=2，
即M(1，2)，
将M(1，2)代入y=kx+b，得k+b=2①
将A(-2，0)代入y=kx+b，得-2k+b=0②
由①②解得k=，b=
（2）解：由(1)知l2:y=x+ ，当x=0时
y= 即OB=
∴S△AOB= OA·OB= ×2× =
在y=-2x+4令y=0，得N(2，0)
又因为A(-2，0)，故AN=4
所以S△AMN= ×AN×ym= ×4×2=4
故SMNOB=S△AMN-S△AOB=4-=.
考查了两条直线的相交问题，以及一次函数图象的点的特征，要熟练掌握．
15、（1）点A的坐标为， 点B的坐标为 （2）图形见解析（3）
【解析】
试题分析：令y=0，则x=2；令x=0，则y=1，即可得A，B两点的坐标；（2）连接AB即可得该函数的图象；（3）根据一次函数的性质即可求得结论.
试题解析：
（1）令，则；
令，则.
∴点A的坐标为，
点B的坐标为.
（2）如图：
（3）
16、 (1)35；；30；；(2)此时气球上升了20min,都位于海拔25m的高度；(3)当时，y最大值为15.
【解析】
（Ⅰ）根据距离=速度×时间，分别计算即可得答案；（Ⅱ）根据上升的高度相同列方程可求出x的值，进而可求出两个气球所在高度；（Ⅲ）设两个气球在同一时刻所在的位置的海拔相差m，由（Ⅱ）可知x=20时，两气球所在高度相同，当0≤x