2024-2025学年江苏省东台市实验中学数学九上开学教学质量检测模拟试题【含答案】

这是一份2024-2025学年江苏省东台市实验中学数学九上开学教学质量检测模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，两地被池塘隔开，小明先在直线外选一点，然后测量出，的中点，并测出的长为．由此，他可以知道、间的距离为（ ）
A．B．C．D．
2、（4分）如图，在中，，，，延长到点，使，交于点，在上取一点，使，连接．有以下结论：①平分；②；③是等边三角形；④，则正确的结论有（ ）
A．1个B．2个C．3个D．4个
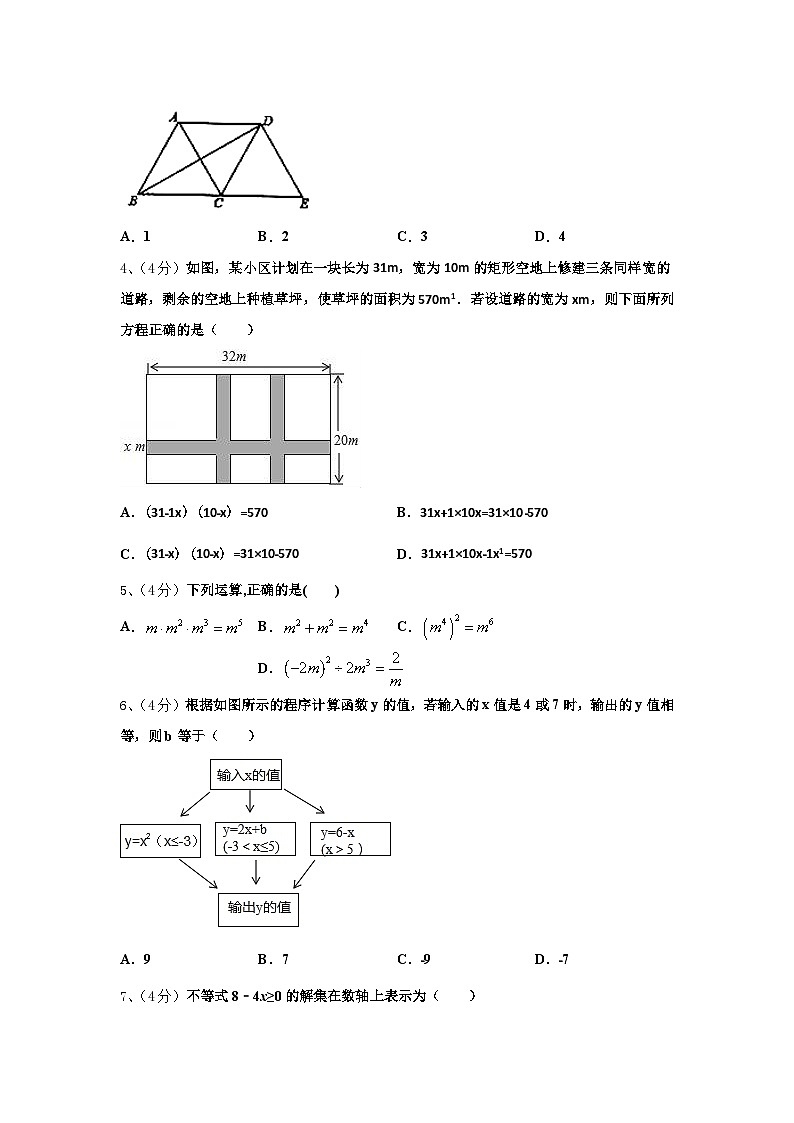
3、（4分）如图所示，等边三角形沿射线向右平移到的位置，连接、，则下列结论：（1）（2）与互相平分（3）四边形是菱形（4），其中正确的个数是（ ）
A．1B．2C．3D．4
4、（4分）如图，某小区计划在一块长为31m，宽为10m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m1．若设道路的宽为xm，则下面所列方程正确的是（ ）
A．（31﹣1x）（10﹣x）=570B．31x+1×10x=31×10﹣570
C．（31﹣x）（10﹣x）=31×10﹣570D．31x+1×10x﹣1x1=570
5、（4分）下列运算,正确的是( )
A．B．C．D．
6、（4分）根据如图所示的程序计算函数y的值，若输入的x值是4或7时，输出的y值相等，则b等于（ ）
A．9B．7C．﹣9D．﹣7
7、（4分）不等式8﹣4x≥0的解集在数轴上表示为（ ）
A．
B．
C．
D．
8、（4分）下列说法正确的是（ ）
A．若你在上一个路口遇到绿灯，则在下一路口必遇到红灯
B．某蓝球运动员2次罚球，投中一个，则可断定他罚球命中的概率一定为50%
C．“明天我市会下雨”是随机事件
D．若某种彩票中奖的概率是1%，则买100张该种彩票一定会中奖
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）过多边形某个顶点的所有对角线，将这个多边形分成个三角形，这个多边形是________.
10、（4分）若直线和直线的交点在第三象限，则m的取值范围是________.
11、（4分）如果关于x的一元二次方程x2﹣6x+c=0（c是常数）没有实根，那么c的取值范围是 ．
12、（4分）已知反比例函数在第一象限的图象如图所示，点A在其图象上，点B为轴正半轴上一点，连接AO、AB，且AO=AB，则S△AOB= .
13、（4分）一次函数 的图象如图所示，则关于的不等式的解集为__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）为深入践行总书记提出的“绿水青山就是金山银山”的重要理念，某学校积极响应号召，进行校园绿化，计划购进、两种树苗共30棵，已知种树苗每棵80元，种树苗每棵50元．设购买种树苗棵，购买两种树苗所需费用为元
（1）求与的函数关系式．
（2）若购买种树苗的数量不少于种树苗数量的2倍，请给出一种费用最少的购买方案，并求出该方案所需的费用．
15、（8分）若关于的一元二次方程有实数根，．
（1）求实数的取值范围；
（2）设，求的最小值．
16、（8分）在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B)，作MN⊥DM，垂足为M，交∠CBE的平分线于点N.
(1)写出点C的坐标；
(2)求证：MD=MN；
(3)连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，其中只有一个结论是正确的，请你指出正确的结论，并给出证明
17、（10分）如图，▱ABCD中，AC为对角线，G为CD的中点，连接AG并廷长交BC的延长线于点F，连接DF，求证：四边形ACFD为平行四边形．
18、（10分）化简求值：(1+)÷，其中x＝﹣1．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）在Rt△ABC中，∠ACB=90°，AE，BD是角平分线，CM⊥BD于M，CN⊥AE于N，若AC=6，BC=8，则MN=_____．
20、（4分）如图，在反比例函数的图象上有四个点，，，，它们的横坐标依次为，，，，分别过这些点作轴与轴的垂线，则图中阴影部分的面积之和为______.
21、（4分）如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为______．
22、（4分）已知直线与直线平行且经过点，则__．
23、（4分）如图，已知一次函数y＝ax+b和y＝kx的图象交于点P(﹣4，﹣2)，则关于x的不等式ax+b≤kx＜1的解集为______.
二、解答题（本大题共3个小题，共30分）
24、（8分）（1）因式分解：；
（2）计算：
25、（10分）如图，在正方形网格中，△TAB 的顶点坐标分别为 T(1，1)、A(2，3)、B(4，2)．
(1)以点 T(1，1)为位似中心，在位似中心的 同侧将△TAB 放大为原来的 3 倍，放大 后点 A、B 的对应点分别为 A'、B'，画出△TA'B'：
(2)写出点 A'、B'的坐标：A'( )、B'（ ）；
(3)在(1)中，若 C(a，b)为线段 AB 上任一 点，则变化后点 C 的对应点 C'的坐标为 ( )．
26、（12分）我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据三角形中位线定理解答．
【详解】
解：∵点M，N分别是AC，BC的中点，
∴AB=2MN=13（m），
故选：C．
本题考查了三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是关键．
2、D
【解析】
先根据等腰直角三角形的性质及已知条件得出∠DAB=∠DBA=30°，则AD=BD，再证明CD是边AB的垂直平分线，得出∠ACD=∠BCD=45°，然后根据三角形外角的性质求出∠CDE=∠BDE=60°即可判断①②；利用差可求得结论：∠CDE=∠BCE-∠ACB=60°，即可判断③；证明△DCG是等边三角形，再证明△ACD≌△ECG，利用线段的和与等量代换即可判断④．
【详解】
解：∵△ABC是等腰直角三角形，∠ACB=90°，
∴∠BAC=∠ABC=45°，
∵∠CAD=∠CBD=15°，
∴∠BAD=∠ABD=45°-15°=30°，
∴BD=AD，
∴D在AB的垂直平分线上，
∵AC=BC，
∴C也在AB的垂直平分线上，
即直线CD是AB的垂直平分线，
∴∠ACD=∠BCD=45°，
∴∠CDE=∠CAD+∠ACD=15°+45°=60°，
∵∠BDE=∠DBA+∠BAD=60°；
∴∠CDE=∠BDE，
即DE平分∠BDC；
所以①②正确；
∵CA=CB，CB=CE，
∴CA=CE，
∵∠CAD=∠CBD=15°，
∴∠BCE=180°-15°-15°=150°，
∵∠ACB=90°，
∴∠ACE=150°-90°=60°，
∴△ACE是等边三角形；
所以③正确；
∵,∠EDC=60°，
∴△DCG是等边三角形，
∴DC=DG=CG，∠DCG=60°，
∴∠GCE=150°-60°-45°=45°，
∴∠ACD=∠GCE=45°，
∵AC=CE，
∴△ACD≌△ECG，
∴EG=AD，
∴DE=EG+DG=AD+DC，
所以④正确；
正确的结论有：①②③④；
故选：D．
本题考查了等腰三角形、全等三角形的性质和判定、等腰直角三角形、等边三角形等特殊三角形的性质和判定，熟练掌握有一个角是60°的等腰三角形是等边三角形这一判定等边三角形的方法，在几何证明中经常运用．
3、D
【解析】
先求出∠ACD=60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；再结合①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD，再根据平移后对应线段互相平行可得∠BDE=∠COD=90°，进而判断④正确.
【详解】
解：如图：∵△ABC，△DCE是等边三角形
∴∠ACB=∠DCE=60°，AC=CD
∴∠ACD=180°-∠ACB-∠DCE=60°
∴△ACD是等边三角形
∴AD=AC=BC，故①正确；
由①可得AD=BC
∵AB=CD
∴四边形ABCD是平行四边形，
∴BD、AC互相平分，故②正确；
由①可得AD=AC=CE=DE故四边形ACED是菱形，即③ 正确
∵四边形ABCD是平行四边形，BA=BC
∴.四边形ABCD是菱形
∴AC⊥BD，AC//DE
∴∠BDE=∠COD=90°
∴BD⊥DE，故④正确
综上可得①②③④正确，共4个.
故选：D
此题主要考查了菱形的判定与性质，以及平移的性质，关键是掌握菱形四边相等，对角线互相垂直.
4、A
【解析】
六块矩形空地正好能拼成一个矩形，设道路的宽为xm，根据草坪的面积是570m1，即可列出方程:(31−1x)(10−x)=570，
故选A.
5、D
【解析】
分别根据同底数幂的乘除运算法则以及幂的乘方和合并同类项法则求出即可．
【详解】
A选项：m•m2•m3=m6，故此选项错误；
B选项：m2+m2=2m2，故此选项错误；
C选项：（m4）2=m8，故此选项错误；
D选项：（-2m）2÷2m3=，此选项正确．
故选：D．
考查了同底数幂的乘除运算法则以及幂的乘方和合并同类项法则等知识，熟练应用运算法则是解题关键．
6、C
【解析】
先求出x=7时y的值，再将x=4、y=-1代入y=2x+b可得答案．
【详解】
∵当x=7时，y=6-7=-1，
∴当x=4时，y=2×4+b=-1，
解得：b=-9，
故选C．
本题主要考查函数值，解题的关键是掌握函数值的计算方法．
7、C
【解析】
先根据不等式的基本性质求出此不等式的解集，在数轴上表示出来，再找出符合条件的选项即可．
【详解】
8﹣4x≥0
移项得，﹣4x≥﹣8，
系数化为1得，x≤1．
在数轴上表示为：
故选：C．
本题考查的是解一元一次不等式及在数轴上表示不等式的解集，解答此类题目时要注意实心圆点与空心圆点的区别．正确求出不等式的解集是解此题的关键．
8、C
【解析】
解：A．若你在上一个路口遇到绿灯，则在下一路口不一定遇到红灯，故本选项错误；
B．某蓝球运动员2次罚球，投中一个，这是一个随机事件，但不能断定他罚球命中的概率一定为50%，故本选项错误；
C．明天我市会下雨是随机事件，故本选项正确；
D．某种彩票中奖的概率是1%，买100张该种彩票不一定会中奖，故该选项错误．
故选C．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
根据n边形从一个顶点出发可引出（n-3）条对角线，可组成n-2个三角形，依此可得n的值.
【详解】
解：设这个多边形是n边形，由题意得，n-2=7，
解得：n=9，
故答案为：9.
本题考查了多边形的对角线，求对角线条数时，直接代入边数n的值计算，而计算边数时，需利用方程思想，解方程求n.
10、m<−1．
【解析】
首先把y=2x-1和y=m-x，组成方程组，求解，x和y的值都用m来表示，根据题意交点坐标在第三象限表明x、y都小于0，即可求得m的取值范围．
【详解】
∵ ，
∴解方程组得： ，
∵直线y=2x−1和直线y=m−x的交点在第三象限，
∴x<0，y<0，
∴m<−1，m<0.5，
∴m<−1.
故答案为：m<−1.
此题考查两条直线相交或平行问题，解题关键在于用m来表示x,y的值.
11、c＞1
【解析】
根据关于x的一元二次方程没有实数根时△＜0，得出△=（-6）2-4c＜0，再解不等式即可．
【详解】
∵关于x的一元二次方程x2-6x+c=0（c是常数）没有实根，
∴△=（-6）2-4c＜0，
即36-4c＜0，
解得：c＞1．
故答案为c＞1．
12、6.
【解析】
根据等腰三角形的性质得出CO=BC，再利用反比例函数系数k的几何意义得出S△AOB即可．
【详解】
过点A作AC⊥OB于点C，
∵AO=AB，
∴CO=BC，
∵点A在其图象上，
∴AC×CO=3，
∴AC×BC=3，
∴S△AOB=6.
故答案为6.
13、x≥1
【解析】
由图象得出解集即可．
【详解】
由图象可得再x轴下方,即x≥1的时候,
故答案为: x≥1．
本题考查一次函数图象的性质,关键在于牢记基础知识．
三、解答题（本大题共5个小题，共48分）
14、（1）；（2）购买种树苗20棵，种树苗10棵费用最少，所需费用为2100元
【解析】
（1）根据总费用=购买A种树苗的费用+购买B种树苗的费用列出关系式即可；
（2）根据一次函数的增减性结合x的取值范围即可解答.
【详解】
解：（1）；
（2）由题意得：，
解得：，
中，
随的增大而增大
时，有最小值，
最小.
此时，.
答：购买种树苗20棵，种树苗10棵费用最少，所需费用为2100元．
本题考查了一次函数的实际应用，根据实际问题列出关系式并运用函数性质求解是解题关键.
15、（1）k≤−2；（2）t的最小值为−1．
【解析】
（1）由一元二次方程存在两实根，可得△≥0，进而求得k的取值范围；
（2）将α+β化为关于k的表达式，根据k的取值范围得出t的取值范围，即可求得的最小值．
【详解】
（1）∵一元二次方程x2−2(2−k)x+k2+12=0有实数根a，β，
∴△≥0，即：1(2−k)2−1(k2+12)≥0，解得：k≤−2；
（2）由根与系数的关系得：a+β=−[−2(2−k)]=1−2k，
∴==−2，
∵k≤−2，
∴−2≤<0，
∴−1≤−2<−2，
∴t的最小值为−1．
本题主要考查一元二次方程根的判别式以及根与系数的关系，掌握（a≠0），有实数根a，β时，则△≥0，a+β=，aβ=，是解题的关键．
16、（1）点的坐标为；（2）见解析；（3）MN平分∠FMB成立，证明见解析
【解析】
（1）根据四边形OBCD是正方形所以点C的坐标应该是C（2，2）；
（2）可通过构建全等三角形来求解．在OD上取OH=OM，通过证三角形DHM和MBN全等来得出DM=MN．
（3）本题也是通过构建全等三角形来求解的．在BO延长线上取OA=CF，通过三角形OAD，FDC和三角形DAM，DMF这两对全等三角形来得出FM和OM，CF的关系，从而得出FM是否是定值．然后再看∠FMN是否与∠NME相等．
【详解】
（1）∵四边形是正方形，，
∴
∴点的坐标为
(2)在OD上取OH=OM，连接HM，
∵OD=OB，OH=OM，
∴HD=MB，∠OHM=∠OMH，
∴∠DHM=180°−45°=135°，
∵NB平分∠CBE，
∴∠NBE=45°，
∴∠NBM=180°−45°=135°，
∴∠DHM=∠NBM，
∵∠DMN=90°，
∴∠DMO+∠NMB=90°，
∵∠HDM+∠DMO=90°，
∴∠HDM=∠NMB，
在△DHM和△MBN中，
，
∴△DHM≌△MBN(ASA)，
∴DM=MN.
(3)MN平分∠FMB成立。证明如下：
在BO延长线上取OA=CF,可证△DOA≌△DCF,△DMA≌△DMF，
FM=MA=OM+CF(不为定值)，∠DFM=∠DAM=∠DFC，
过M作MP⊥DN于P，则∠FMP=∠CDF，
由(2)可知∠NMF+∠FMP=∠PMN=45°，
∠NMB=∠MDH,∠MDO+∠CDF=45°，
进一步得∠NMB=∠NMF，即MN平分∠FMB.
此题考查角平分线的性质，正方形的性质，坐标与图形性质，全等三角形的判定与性质，解题关键在于作辅助线
17、见解析
【解析】
根据平行四边形的性质证出∠ADC=∠FCD，然后再证明△ADG≌△FCG可得AD=FC，根据一组对边平行且相等的四边形是平行四边形可得结论；
【详解】
证明：∵在▱ABCD中，AD∥BF．
∴∠ADC=∠FCD．
∵G为CD的中点，
∴DG=CG．
在△ADG和△FCG中，
，
∴△ADG≌△FCG（ASA）
∴AD=FC．
又∵AD∥FC，
∴四边形ACFD是平行四边形．
此题主要考查了平行四边形的判定和性质、全等三角形的判定与性质；熟练掌握平行四边形的判定与性质，证明三角形全等是解题的关键．
18、，-2.
【解析】
根据分式的加法和除法可以化简题目中的式子，然后将x的值代入化简后的式子即可解答本题．
【详解】
(1+)÷ ，
＝
＝，
当x＝﹣1时，原式＝＝﹣2．
本题考查分式的化简求值，解答本题的关键是明确分式的化简求值的方法．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1．
【解析】
延长CM交AB于G，延长CN交AB于H，证明△BMC≌△BMG，得到BG=BC=8，CM=MG，同理得到AH=AC=6，CN=NH，根据三角形中位线定理计算即可得出答案．
【详解】
如图所示，延长CM交AB于G，延长CN交AB于H，
∵∠ACB=90°，AC=6，BC=8，
∴由勾股定理得AB=10，
在△BMC和△BMG中,
，
∴△BMC≌△BMG，
∴BG=BC=8，CM=MG，
∴AG=1，
同理，AH=AC=6，CN=NH，
∴GH=4，
∵CM=MG，CN=NH，
∴MN=GH=1.
故答案为：1.
本题考查了等腰三角形的判定和性质、三角形的中位线.利用全等证出三角形BCE与三角形ACH是等腰三角形是解题的关键.
20、2
【解析】
由题意，图中阴影部分的面积之和＝×矩形AEOF的面积，根据比例系数k的几何意义即可解决问题；
【详解】
解：如图，∵反比例函数的解析式为，
∴矩形AEOF的面积为1．
由题意，图中阴影部分的面积之和＝×矩形AEOF的面积＝2，
故答案为2．
本题考查反比例函数的几何意义，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
21、1.1
【解析】
试题解析：∵∠AFB=90°，D为AB的中点，
∴DF=AB=2.1，
∵DE为△ABC的中位线，
∴DE=BC=4，
∴EF=DE-DF=1.1，
故答案为1.1．
直角三角形斜边上的中线性质：在直角三角形中，斜边上的中线等于斜边的一半和三角形的中位线性质：三角形的中位线平行于第三边，并且等于第三边的一半．
22、2
【解析】
由一次函数y=kx+b的图象与正比例函数y=2x的图象平行得到k=2，然后把点A（1，2）代入一次函数解析式可求出b的值．
【详解】
直线与直线平行，
，
，
把点代入得，解得；
，
故答案为：2
本题主要考查了两条直线相交或平行问题，待定系数法，解答此类题关键是掌握若直线y=k1x+b1与直线y=k2x+b2平行，则k1=k2；若直线y=k1x+b1与直线y=k2x+b2相交，则由两解析式所组成的方程组的解为交点坐标．
23、﹣4≤x＜1
【解析】
先利用待定系数法求出y＝kx的表达式，然后求出y＝1时对应的x值，再根据函数图象得出结论即可．
【详解】
解：∵已知一次函数y＝ax+b和y＝kx的图象交于点P(﹣4，﹣1)，
∴﹣4k＝﹣1，
解得：k＝，
∴解析式为y＝x，
当y＝1时，x＝1，
∵由函数图象可知，当x≥﹣4时一次函数y＝ax+b在一次函数y＝kx图象的下方，
∴关于x的不等式ax+b≤kx＜1的解集是﹣4≤x＜1．
故答案为：﹣4≤x＜1．
本题主要考查两个一次函数的交点问题，能够数形结合是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）y（x-2）2；（2） ．
【解析】
（1）先提公因式，再利用完全平方公式矩形因式分解；
（2）根据分式的减法运算法则计算．
【详解】
解：（1）x2y-4xy+4y
=y（x2-4x+4）
=y（x-2）2；
（2）
=
=
=
= ．
故答案为：（1）y（x-2）2；（2） ．
本题考查因式分解、分式的加减运算，掌握提公因式法、完全平方公式因式分解、分式的加减法法则是解题的关键．
25、（1）详见解析；（1）A′（4，7），B′（10，4）（3）(3a-1,3b-1)
【解析】
（1）根据题目的叙述，在位似中心的同侧将△TAB放大为原来的3倍，得到对应点坐标，正确地作出图形即可，
（1）根据图象确定各点的坐标即可．
（3）根据（1）中变换的规律，即可写出变化后点C的对应点C′的坐标．
【详解】
解：（1）如图所示：
（1）点A′，B′的坐标分别为：A′（4，7），B′（10，4）；
故答案为：(4，7)；(10，4)；
（3）变化后点C的对应点C′的坐标为：C′（3a-1，3b-1）
故答案为：3a-1，3b-1．
本题考查了位似变换作图的问题，正确理解位似变换的定义，会进行位似变换的作图是解题的关键．
26、（1）证明见解析；（2）四边形EFGH是菱形，证明见解析；（3）四边形EFGH是正方形.
【解析】
（1）如图1中，连接BD，根据三角形中位线定理只要证明EH∥FG，EH=FG即可．
（2）四边形EFGH是菱形．先证明△APC≌△BPD，得到AC=BD，再证明EF=FG即可．
（3）四边形EFGH是正方形，只要证明∠EHG=90°，利用△APC≌△BPD，得∠ACP=∠BDP，即可证明∠COD=∠CPD=90°，再根据平行线的性质即可证明．
【详解】
（1）证明：如图1中，连接BD．
∵点E，H分别为边AB，DA的中点，
∴EH∥BD，EH=BD，
∵点F，G分别为边BC，CD的中点，
∴FG∥BD，FG=BD，
∴EH∥FG，EH=GF，
∴中点四边形EFGH是平行四边形．
（2）四边形EFGH是菱形．
证明：如图2中，连接AC，BD．
∵∠APB=∠CPD，
∴∠APB+∠APD=∠CPD+∠APD，
即∠APC=∠BPD，
在△APC和△BPD中，
∵AP=PB，∠APC=∠BPD，PC=PD，
∴△APC≌△BPD，
∴AC=BD．
∵点E，F，G分别为边AB，BC，CD的中点，
∴EF=AC，FG=BD，
∵四边形EFGH是平行四边形，
∴四边形EFGH是菱形．
（3）四边形EFGH是正方形．
证明：如图2中，设AC与BD交于点O．AC与PD交于点M，AC与EH交于点N．
∵△APC≌△BPD，
∴∠ACP=∠BDP，
∵∠DMO=∠CMP，
∴∠COD=∠CPD=90°，
∵EH∥BD，AC∥HG，
∴∠EHG=∠ENO=∠BOC=∠DOC=90°，
∵四边形EFGH是菱形，
∴四边形EFGH是正方形．
考点：平行四边形的判定与性质；中点四边形．
题号
一
二
三
四
五
总分
得分