2024-2025学年江苏省海安县白甸镇初级中学九上数学开学经典试题【含答案】

这是一份2024-2025学年江苏省海安县白甸镇初级中学九上数学开学经典试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
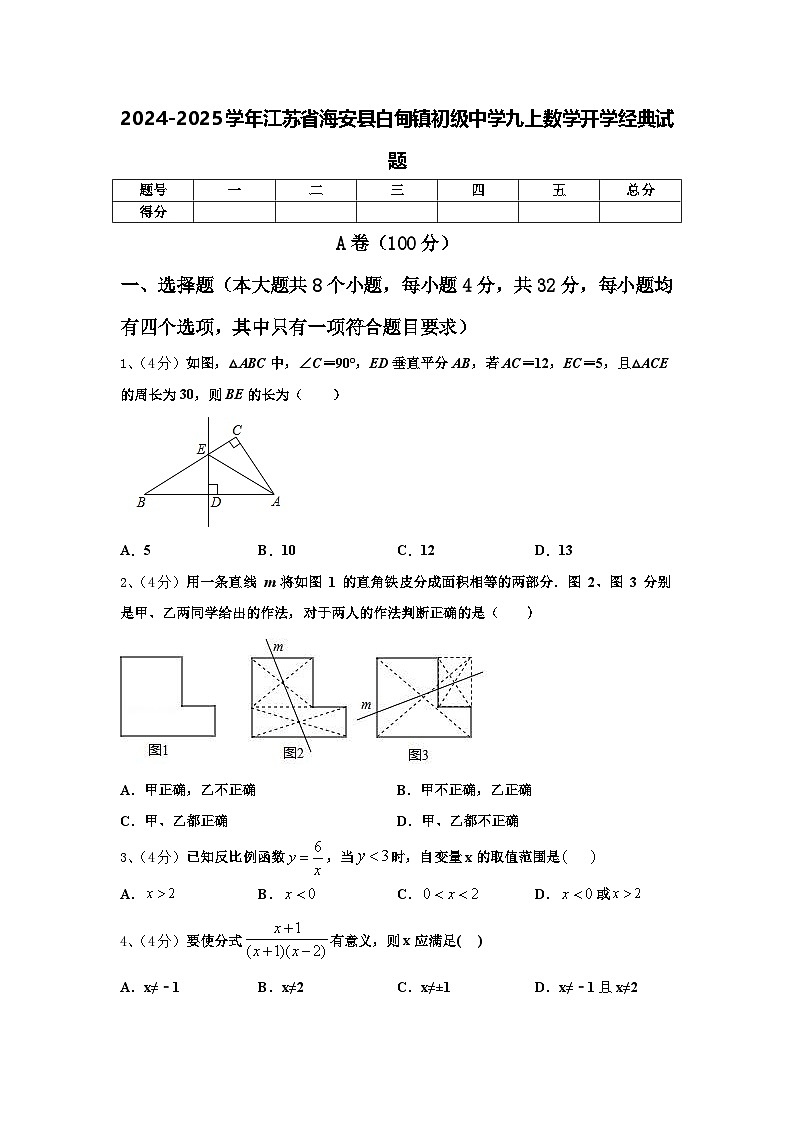
1、（4分）如图，△ABC中，∠C＝90°，ED垂直平分AB，若AC＝12，EC＝5，且△ACE的周长为30，则BE的长为（ ）
A．5B．10C．12D．13
2、（4分）用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分．图 2、图 3 分别是甲、乙两同学给出的作法，对于两人的作法判断正确的是（ ）
A．甲正确，乙不正确B．甲不正确，乙正确
C．甲、乙都正确D．甲、乙都不正确
3、（4分）已知反比例函数，当时，自变量x的取值范围是
A．B．C．D．或
4、（4分）要使分式有意义，则x应满足( )
A．x≠﹣1B．x≠2C．x≠±1D．x≠﹣1且x≠2
5、（4分）某园林队原计划由6名工人对180平方米的区域进行绿化,由于施工时增加了2名工人,结果比原计划提前3小时完成任务,若每人每小时绿化的面积相同，求每人每小时绿化的面积。若设每人每小时绿化的面积为平方米，根据题意下面所列方程正确的是（ ）
A．B．
C．D．
6、（4分）已知直线y1＝2x与直线y2＝﹣2x+4相交于点A．有以下结论：①点A的坐标为A（1，2）；②当x＝1时，两个函数值相等；③当x＜1时，y1＜y2；④直线y1＝2x与直线y2＝2x﹣4在平面直角坐标系中的位置关系是平行．其中正确的是（ ）
A．①③④B．②③C．①②③④D．①②③
7、（4分）如图，矩形ABCD中，对角线AC，BD相交于点O，下列结论不一定成立的是
A．
B．
C．
D．
8、（4分）如图，将▱ABCD沿对角线AC进行折叠，折叠后点D落在点F处，AF交BC于点E，有下列结论：①△ABF≌△CFB；②AE＝CE；③BF∥AC；④BE＝CE，其中正确结论的个数是( )
A．1B．2C．3D．4
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分） “我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=0.5千米，则该沙田的面积为________________平方千米．
10、（4分）当时，分式的值是________.
11、（4分）如果在五张完全相同的纸片背后分别写上平行四边形、矩形、菱形、正方形、等腰梯形，打乱后随机抽取其中一张，那么抽取的图形既是轴对称图形又是中心对称图形的概率等于_____．
12、（4分）已知关于的方程会产生增根，则__________．
13、（4分）如图，四边形ABCD是平行四边形，O是对角线AC与BD的交点，AB⊥AC，若AB=8，AC=12，则BD的长是．
三、解答题（本大题共5个小题，共48分）
14、（12分）在“国学经典”主题比赛活动中，甲、乙、丙三位同学的三项比赛成绩如下表（单位：分）．
（1）若“国学知识”、“现场写作”“经典诵读”分别按30%，20%，50%的比例计入该同学的比赛得分，请分别计算甲、乙两位同学的得分；
（2）若甲同学的得分是80分，乙同学的得分是84分，则丙同学的得分是______分．
15、（8分）如图，正比例函数y1=kx与-次函数y2=mx+n的图象交于点A(3，4)，一次函数y2的图象与x轴，y轴分别交于点B，点C，且0A=OC．
(1)求这两个函数的解析式；
(2)求直线AB与两坐标轴所围成的三角形的面积．
16、（8分）一辆货车从A地运货到240km的B地，卸货后返回A地，如图中实线是货车离A地的路程y（km）关于出发后的时间x（h）之间的函数图象．货车出发时，正有一个自行车骑行团在AB之间，距A地40km处，以每小时20km的速度奔向B地．
（1）货车去B地的速度是 ，卸货用了 小时，返回的速度是 ；
（2）求出自行车骑行团距A地的路程y（km）关于x的函数关系式，并在此坐标系中画出它的图象；
（3）求自行车骑行团与货车迎面相遇，是货车出发后几小时后，自行车骑行团还有多远到达B地．
17、（10分）如图，AD是△ABC边BC上的高，用尺规在线段AD上找一点E，使E到AB的距离等于ED(不写作法，保留作图痕迹)
18、（10分）一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1千米，出租车离甲地的距离为y2千米，两车行驶的时间为x小时，y1、y2关于x的函数图像如下图
所示：
（1）根据图像，直接写出y1、y2关于x的函数关系式；
（2）若两车之间的距离为S千米，请写出S关于x的函数关系式；
（3）甲、乙两地间有A、B两个加油站，相距200千米，若客车进入A加油站时，出租车恰好进入B加油站，求A加油站离甲地的距离.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜0；②a＞0；③关于x的方程kx﹣x=a﹣b的解是x=3；④当x＞3时，y1＜y2中．则正确的序号有____________．
20、（4分）直线与坐标轴围成的图形的面积为________.
21、（4分）己知三角形三边长分别为，，，则此三角形的最大边上的高等于_____________.
22、（4分）若二次根式有意义，则x的取值范围是 ▲ ．
23、（4分）已知四边形是矩形，点是边的中点，以直线为对称轴将翻折至，联结，那么图中与相等的角的个数为_____________
二、解答题（本大题共3个小题，共30分）
24、（8分）在一个布口袋里装着白、红、黑三种颜色的小球，它们除颜色之外没有任何其它区别，其中有白球3只、红球2只、黑球1只．袋中的球已经搅匀．
（1）闭上眼睛随机地从袋中取出1只球，求取出的球是黑球的概率；
（2）若取出的第1只球是红球，将它放在桌上，闭上眼睛从袋中余下的球中再随机地取出1只球，这时取出的球还是红球的概率是多少？
（3）若取出一只球，将它放回袋中，闭上眼睛从袋中再随机地取出1只球，两次取出的球都是白球概率是多少？（用列表法或树状图法计算）
25、（10分）有一工程需在规定日期x天内完成，如果甲单独工作刚好能够按期完成：如果乙单独工作就要超过规定日期3天．
（1）甲的工作效率为 ，乙的工作效率为 ．（用含x的代数式表示）
（2）若甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成，求x的值．
26、（12分）解下列方程:
(1); (2).
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
ED垂直平分AB，BE＝AE，在通过△ACE的周长为30计算即可
【详解】
解：∵ED垂直平分AB，
∴BE＝AE，
∵AC＝12，EC＝5，且△ACE的周长为30，
∴12+5+AE＝30，
∴AE＝13，
∴BE＝AE＝13，
故选：D．
本题考查了线段的垂直平分线的性质，熟知线段垂直平分线上的点到线段两端点的距离相等是解答此题的关键．
2、C
【解析】
根据图形中所画出的虚线，可以利用图形中的长方形、梯形的面积比较得出直线两旁的面积的大小关系．
【详解】
如图：图形2中，直线m经过了大长方形和小长方形的对角线的交点，所以两旁的图形的面积都是大长方形和小长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即甲做法正确；
图形3中，经过大正方形和图形外不添补的长方形的对角线的交点，直线两旁的面积都是大正方形面积的一半-添补的长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即乙做法正确．
故选C．
此题主要考查了中心对称，根据图形中的割补情况，抓住经过对角线的交点的直线都能把长方形分成面积相等的两部分这一特点，即可解决问题．
3、D
【解析】
根据函数解析式中的系数推知函数图象经过第一、三象限，结合函数图象求得当时自变量的取值范围．
【详解】
解：反比例函数的大致图象如图所示，
当时自变量的取值范围是或．
故选：．
考查了反比例函数的性质，解题时，要注意自变量的取值范围有两部分组成．
4、D
【解析】
试题分析：当（x+1）（x-2）时分式有意义，所以x≠-1且x≠2，故选D．
考点：分式有意义的条件．
5、A
【解析】
设每人每小时的绿化面积为x平方米，等量关系为：6名工人比8名工人完成任务多用3小时，据此列方程即可．
【详解】
解：设每人每小时的绿化面积为x平方米，
由题意得，
故选：A．
本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．
6、C
【解析】
∵将A（1，2）代入y1和y2中可得左边＝右边，
∴①是正确的；
∵当x=1时，y1=2,y2=2,故两个函数值相等，
∴②是正确的；
∵x