2024年春 中考数学 习题课件 第三部分 函数 第11课时 一次函数的实际应用

这是一份2024年春 中考数学 习题课件 第三部分 函数 第11课时 一次函数的实际应用，文件包含他们那时候多有趣啊含课后作业课外练习pptx、《他们那时候多有趣啊》教案含教学反思docx、17《他们那时候多有趣啊》说课稿doc、机器人总动员mp4、流浪地球mp4、GlowSansSC-Normal-Heavyotf、SourceHanSansCN-Normalotf等7份课件配套教学资源，其中PPT共29页， 欢迎下载使用。
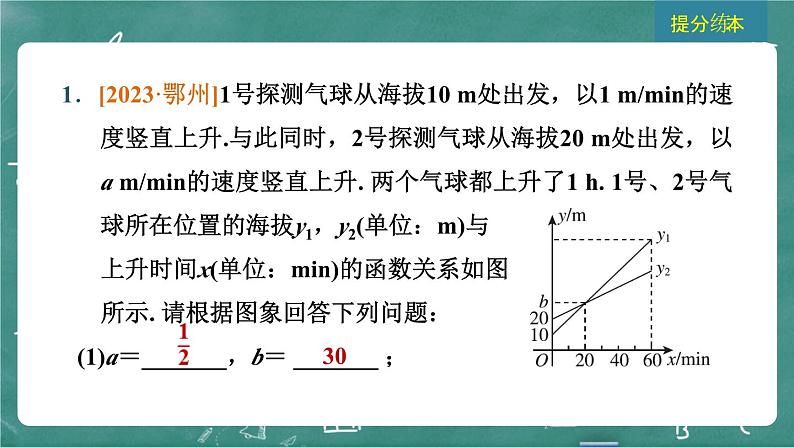
1．[2023·鄂州]1号探测气球从海拔10 m处出发，以1 m/min的速度竖直上升.与此同时，2号探测气球从海拔20 m处出发，以a m/min的速度竖直上升. 两个气球都上升了1 h. 1号、2号气球所在位置的海拔y1，y2(单位：m)与上升时间x(单位：min)的函数关系如图所示. 请根据图象回答下列问题：(1)a＝_______，b＝ _______ ；
(2)请分别求出y1，y2与x 的函数关系式；
(3)当上升多长时间时，两个气球的海拔竖直高度差为5 m ？
2．[2023·宜昌]某食用油的沸点温度远高于水的沸点温度. 小聪想用刻度不超过100 ℃的温度计测算出这种食用油的沸点温度. 在老师的指导下，他在锅中倒入一些这种食用油均匀加热，并每隔10 s 测量一次锅中油温，得到的数据记录如下：
(1)如图，小聪在直角坐标系中描出了表中数据对应的点. 经老师介绍，在这种食用油达到沸点前，锅中油温y(单位：℃)与加热的时间t(单位：s)符合初中学习过的某种函数关系，填空：可能是________函数关系(请选填“正比例”“一次” “二次”“反比例”)；
(2)根据以上判断，求y 关于t 的函数解析式；
(3)当加热110 s 时，油沸腾了，请推算这种食用油的沸点温度.
解：当t＝110 时，y＝2×110＋10＝230.∴推算这种食用油的沸点温度为230℃ .
3．[2023·荆门]某文体商店计划购进一批同种型号的篮球和同种型号的排球，每一个排球的进价是每一个篮球的进价的90%，用3 600元购买排球的个数要比用3 600元购买篮球的个数多 10个.(1)问每一个篮球、排球的进价各是多少元？
(2)该文体商店计划购进篮球和排球共100个，且排球个数不低于篮球个数的3倍，篮球的售价定为每一个100元，排球的售价定为每一个90元. 若该批篮球、排球都能卖完，问该文体商店应购进篮球、排球各多少个才能获得最大利润？最大利润是多少？
4．一种弹簧秤最大能称 10 kg 的物体，不挂物体时弹簧的长为12 cm，每挂重1 kg 的物体，弹簧伸长0.5 cm，在弹性限度内，挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )A. y＝12 －0.5x B. y＝12＋0.5xC. y＝10＋0.5x D. y＝0.5x
5．[2023·贵州]今年“五一”假期，小星一家驾车前往黄果树旅游，在行驶过程中，汽车离黄果树景点的路程y(km)与所用时间x(h)之间的函数关系的图象如图所示，下列说法正确的是( )A. 小星家离黄果树景点的路程为50 kmB. 小星从家出发第1 小时的平均速度为75 km/hC. 小星从家出发2 h 后离景点的路程为125 kmD. 小星从家到黄果树景点共用了3 h
6．[2023·聊城]甲乙两地相距a千米，小亮8:00乘慢车从甲地去乙地，10分钟后小莹乘快车从乙地赶往甲地. 两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示，则小亮与小莹相遇的时刻为( )A. 8：28 B. 8：30C. 8：32 D. 8：35
答案： A
7．[2023·威海]一辆汽车在行驶过程中，其行驶路程y(千米)与行驶时间x(时)之间的函数关系如图所示. 当0≤x≤0.5时，y与x 之间的函数解析式为y＝60x；当0.5≤x≤2时，y与x之间的函数解析式为____________.
8．[2023·陕西]经验表明，树在一定的成长阶段，其胸径(树的主干在地面以上1.3 m处的直径)越大，树就越高. 通过对某种树进行测量研究，发现这种树的树高y(m)是其胸径x(m)的一次函数. 已知这种树的胸径为0.2 m时，树高为20 m；这种树的胸径为0.28 m时，树高为22 m.
(1)求y与x之间的函数解析式；
(2)当这种树的胸径为0.3 m时，其树高是多少？
解：当x＝0.3 时，y＝25×0.3＋15＝22.5.∴当这种树的胸径为0.3 m 时，其树高为22.5 m.
9．2023年7月28日至8月8日，第31届世界大学生运动会在成都举行.“当好东道主，热情迎嘉宾”，成都某知名小吃店计划购买A，B 两种食材制作小吃. 已知购买1千克A种食材和1千克B种食材共需68元，购买5千克A种食材和3千克B种食材共需280元.
(1)求A，B 两种食材的单价.
(2)该小吃店计划购买两种食材共36千克，其中购买A种食材千克数不少于B种食材千克数的2倍，当A，B 两种食材分别购买多少千克时，总费用最少？并求出最少总费用.
解：设购买A种食材的质量为m千克，总费用为w元，则购买B种食材的质量为(36－m)千克.由题意得w＝38m＋30(36－m)＝8m＋1 080，∵ m≥2(36－m)，∴ 24≤m﹤36. ∵ 8﹥0，∴w随m的增大而增大.∴当m＝24 时，w 有最小值，最小值为8×24＋1 080＝1 272.此时36－m＝36－24＝12.答：A种食材购买24千克，B种食材购买12千克时，总费用最 少，为1 272元．
10．[2023·广元]某移动公司推出A，B 两种电话计费方式.
(1)设一个月内用移动电话主叫时间为t min，根据上表，分别写出在不同时间范围内，方式A、方式B的计费金额关于t的函数解析式.
(2)若你预计每月主叫时间为350 min，你将选择A，B哪种计费方式？并说明理由.
解：选择方式B. 理由如下：当每月主叫时间为350 min 时，y1＝0.25×350＋28＝115.5，y2＝108.∵ 115.5﹥108，∴选择方式B.
(3)请你根据月主叫时间t的不同范围，直接写出最省钱的计费 方式.
解：当0≤t﹤320 时，方式A 更省钱；当t＝320 时，方式A 和方式B 的计费金额相同；当t﹥320 时，方式B 更省钱.
11．[新视角·方案设计题]某校组织师生参加夏令营活动，现准备租用A，B两型客车(每种型号的客车至少租用一辆). A型车每辆租金500元，B型车每辆租金600元. 若5辆A型和2辆B 型车坐满后共载客310人；3辆A型和4辆B型车坐满后共载客340人.
(1)每辆A型车、B型车坐满后各载客多少人？
(2)若该校计划租用A型和B型两种客车共10 辆，总租金不高于 5 500元，并将全校420人载至目的地. 该校有几种租车方案？哪种租车方案最省钱？
∵ m是正整数，∴ m 可取5，6，7，8，共有4种方案.设总租金为w元.根据题意，得w＝500m＋600(10－m)＝－100m＋6 000.∵－100﹤0，∴ w 随m 的增大而减小.∴当m＝8 时，w 最小. 此时10－m＝2.答：该校有4种租车方案. 租用A 型车8 辆，租用B型车2 辆最省钱.
(3)在这次活动中，学校除租用A，B两型客车外，又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米，甲车从学校出发0.5小时后，乙车才从学校出发，却比甲车早0.5 小时到达目的地. 如图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象. 根据图象信息，求甲、乙两车第一次相遇后，t 为何值时两车相距25千米.