





所属成套资源:【提分练本】中考数学二轮专题复习
2024年春 中考数学 习题课件 第五部分 图形的变化 第26课时 解直角三角形
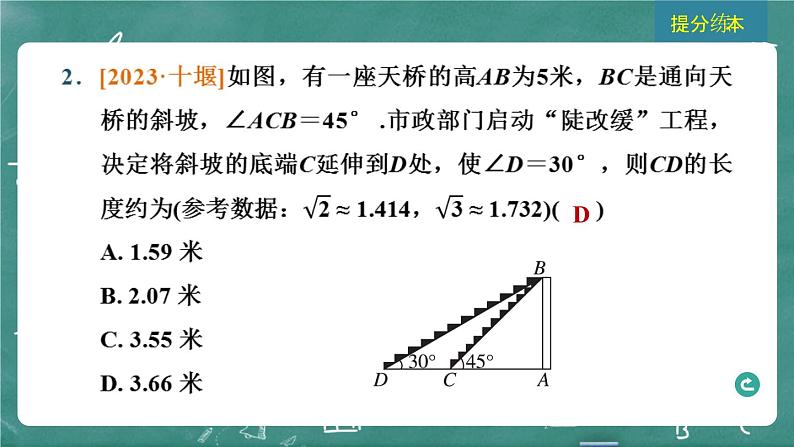
展开
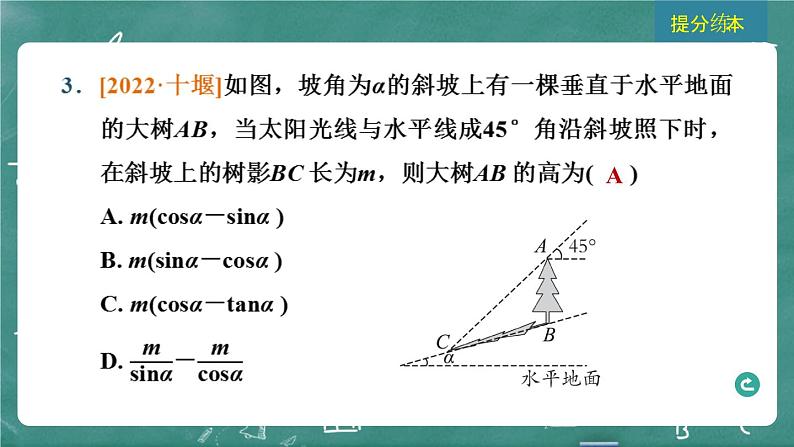
这是一份2024年春 中考数学 习题课件 第五部分 图形的变化 第26课时 解直角三角形,共24页。
4.[2022·黄冈、孝感、咸宁]如图,有甲、乙两座建筑物,从甲建筑物A点处测得乙建筑物D点的俯角α为45°,C点的俯角β为58°,BC为两座建筑物的水平距离. 已知乙建筑物的高度CD 为6 m,则甲建筑物的高度AB 为_______m(sin 58°≈ 0.85,cs 58°≈ 0.53,tan 58°≈ 1.60,结果保留整数).
6.2023年5月30日,“神舟十六号”航天飞船成功发射. 如图,飞船在离地球大约330 km 的圆形轨道上,当飞船运行到地球表面P 点的正上方F 点时,从飞船上直接看到地球表面一个最远的点是点Q. 在Rt△OQF 中,OP=OQ ≈ 6 400 km(参考数据:cs 16°≈ 0.96,cs 18°≈ 0.95,cs 20°≈0.94,cs 22°≈ 0.93,π≈ 3.14).
(1)求cs α 的值(精确到0.01);
(2)在⊙O中,求PQ的长(结果取整数).
7.[2023·荆门]如图,一艘船由西向东航行,在A处测得北偏东60°方向上有一座灯塔C,再向东继续航行60 km到达B 处,这时测得灯塔C在北偏东 30°方向上,已知在灯塔C的周围47 km 内有暗礁,问这艘船继续向东航行是否安全?
8.[2023·恩施州]小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点A,B处测出点D的仰角度数,可以求出信号塔DE的高.如图,AB的长为5m,高BC为3m.他在点A处测得点D的仰角为45°,在点B处测得点D的仰角为38.7°,A,B,C,D,E 在同一平面内.
你认为小王同学能求出信号塔DE 的高吗?若能,请求出信号塔DE的高;若不能,请说明理由(参考数据:sin 38.7°≈0.625,cs 38.7°≈ 0.780,tan 38.7°≈ 0.80,结果保留整数).
解:能求出信号塔DE 的高.过点B 作BF⊥DE,垂足为点F.∵∠ACB=90°,∠AED=90°,∴四边形BCEF是矩形.∴ CE=BF,EF=BC=3 m.
11.如图,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,
若已知:杠杆AB=6米,AO∶OB=2∶1,支架OM⊥EF, OM=3 米,AB可以绕着点O自由旋转,当点A旋转到如图所示位置时∠AOM=45°,此时点B到水平地面EF的距离为______米(结果保留根号).
13.[2023·凉山州]超速容易造成交通事故.高速公路管理部门在某隧道内的C,E两处安装了测速仪,该段隧道的截面示意图如图所示,图中所有点都在同一平面内,且A,D, B,F在同一直线上.点C,点E到AB的距离分别为CD, EF,且CD=EF=7 m,CE=895 m,在C处测得A点的俯角为30°,在E处测得B点的俯角为45°,小型汽车从点A行驶到点B所用时间为45 s.
(1)求A,B两点之间的距离(结果精确到1 m).
解:没有超速. 理由如下:∵ 900÷45=20(m/s),∴小型汽车每小时行驶约20×3 600=72 000(m).∵ 72 000 m=72 km,72﹤80,∴小型汽车从点A 行驶到点B 没有超速.
14.[情境题·生活应用]为了美化环境,提高民众的生活质量,市政府在三角形花园ABC边上修建一个四边形人工湖泊ABDE,并沿湖泊修建了人行步道.如图,点C在点A的正东方向170米处,点E在点A的正北方向,点B,D都在点C 的正北方向,BD长为100米,点B在点A的北偏东30°方向,点D在点E的北偏东58°方向.
(1)求步道DE 的长度;
(2)点D处有一个小商店,某人从点A出发沿人行步道去商店购物,可以经点B到达点D,也可以经点E到达点D,请通过计算说明他走哪条路较近.(结果精确到个位,参考数据: sin 58°≈ 0.85,cs 58°≈0.53,tan 58°≈ 1.60,3≈ 1.73)
相关课件
这是一份2024年春 中考数学 习题课件 第四部分 图形的性质 第23课时 与圆有关的计算,共10页。PPT课件主要包含了1求OC的长等内容,欢迎下载使用。
这是一份2024年春 中考数学 习题课件 第四部分 图形的性质 第22课时 与圆有关的位置关系,共22页。
这是一份2024年春 中考数学 习题课件 第四部分 图形的性质 第21课时 圆的基本性质,共22页。










