13高中数学新教材一轮复习课堂导学案（双曲线一）及答案

这是一份13高中数学新教材一轮复习课堂导学案（双曲线一）及答案，文件包含13高中数学新教材课堂导学案双曲线一及答案doc、13高中数学新教材课堂导学案双曲线一doc等2份学案配套教学资源，其中学案共11页， 欢迎下载使用。
【知识点】
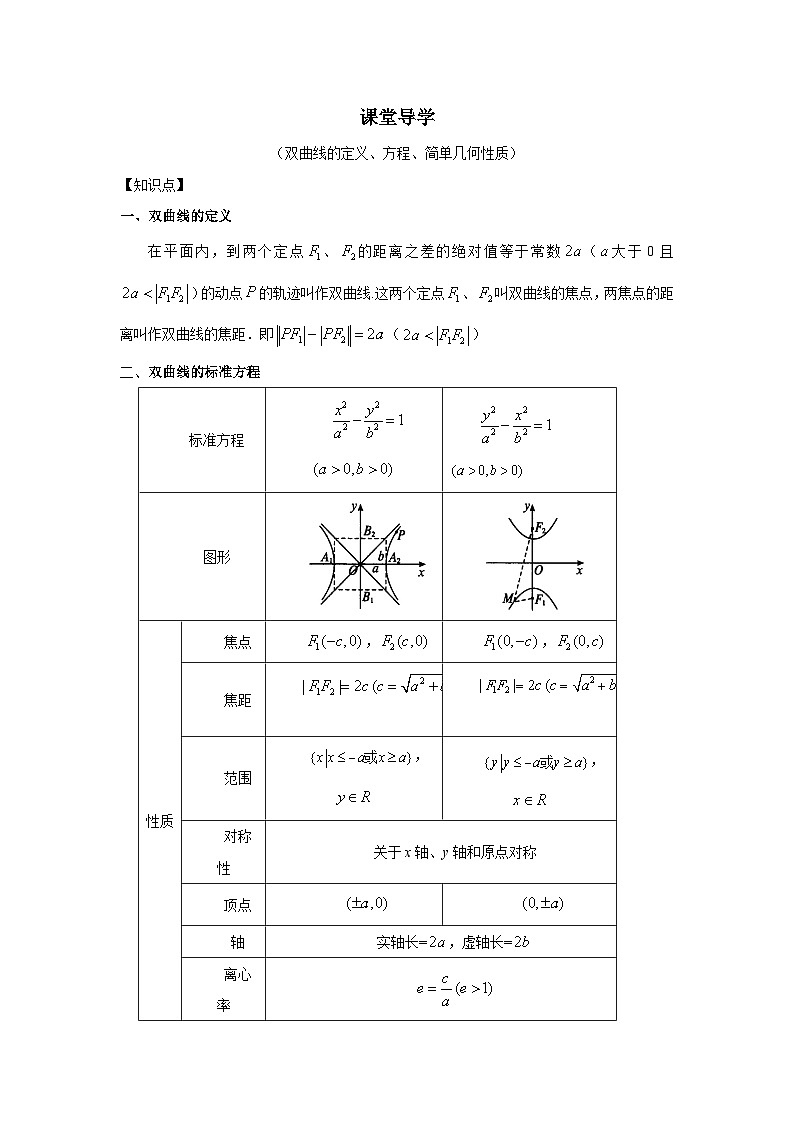
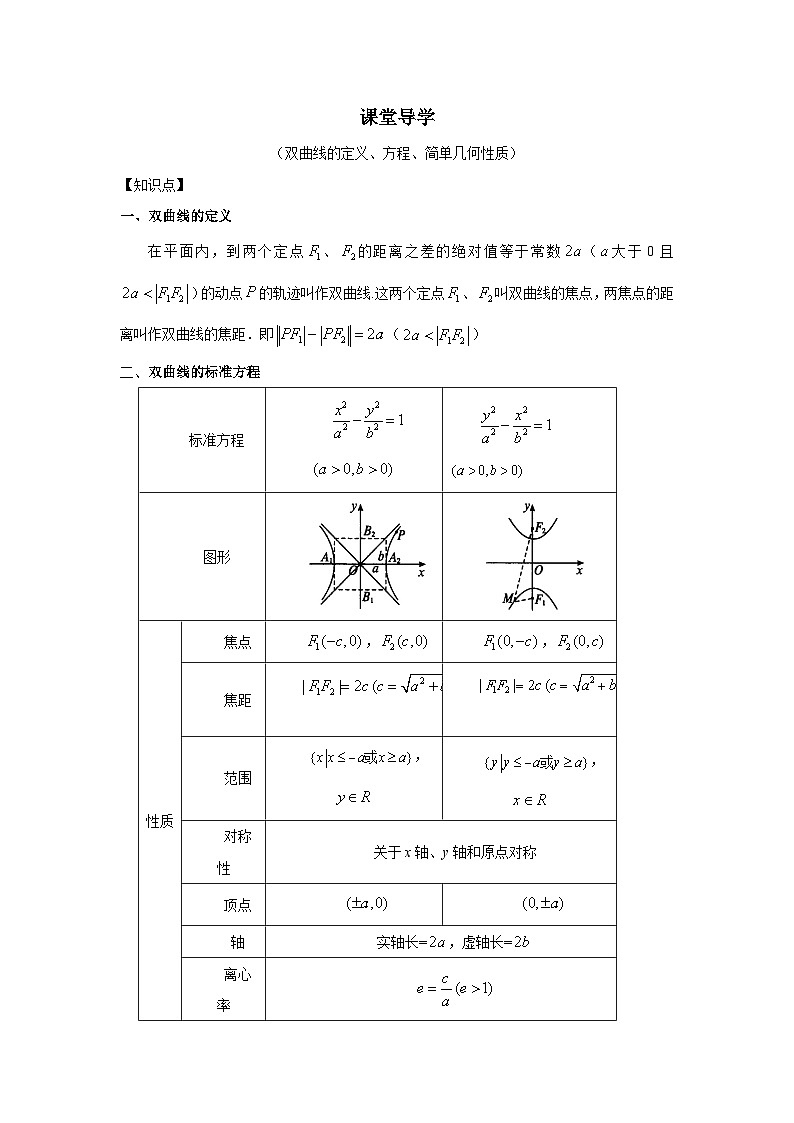
一、双曲线的定义
在平面内，到两个定点、的距离之差的绝对值等于常数（大于0且）的动点的轨迹叫作双曲线.这两个定点、叫双曲线的焦点，两焦点的距离叫作双曲线的焦距．即（）
二、双曲线的标准方程
【典例】
例1． （2021全国Ⅰ）在平面直角坐标系中,已知点、，，点的轨迹为，则的方程为 ；
例2．是双曲线上一点，、是双曲线的两个焦点，且，
求的值．
分析：利用双曲线的定义求解．
解：在双曲线中，，，故．
由是双曲线上一点，得．
∴或．
又，得．
说明：本题容易忽视这一条件，而得出错误的结论或．
例3．如右图所示，为双曲线：的左焦点，双曲线上的点与()关于轴对称，则的值为( C )
A．9 B．16 C．18 D．27
例4．已知曲线C：mx2＋ny2＝1，下列结论不正确的是（ ）
A．若m＞n＞0，则C是椭圆，其焦点在y轴上
B．若m＝n＞0，则C是圆，其半径为
C．若mn＜0，则C是双曲线，其渐近线方程为y＝±x
D．若m＝0，n＞0，则C是两条直线
【答案】B
【解析】
【分析】
就不同的取值结合曲线方程的形式逐项判断后可得正确的选项.
【详解】
对于A，当m＞n＞0时，有，
方程化为，表示焦点在y轴上的椭圆，故A正确；
对于B，由m＝n＞0，方程变形为，
该方程表示半径为的圆，故B错误；
对于C，由mn＜0知曲线表示双曲线，其渐近线方程为，故C正确；
对于D，当m＝0，n＞0时，方程变为ny2＝1表示两条直线，故D正确．
故选：B.
例5．已知实数x，y满足，则的取值范围为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
由已知条件画出曲线，利用数形结合即可求解.
【详解】
曲线由三段曲线组成，分别是：双曲线､圆､双曲线，
其中是那两段双曲线的渐近线，曲线如下图所示，
，其中代表曲线C上任一点到直线的距离，距离的最大值即为圆的半径，双曲线无限趋近于渐近线，
由此可知距离，故的取值范围为，
故选：.
【练习】
一、选择题
1．（2022·广西·钦州一中高二期中（文））已知平面内两定点，，下列条件中满足动点的轨迹为双曲线的是（ ）
A．B．
C．D．
【答案】C
【解析】
【分析】
由双曲线的定义即可求解.
【详解】
解：由题意，因为，
所以由双曲线的定义知，当时，动点的轨迹为双曲线，
故选：C.
2．动点到两定点、的距离之差等于6，则动点的轨迹方程是（ D ）
A．B． C．D．
3．双曲线方程为，则它的右焦点坐标为（ C ）
A、B、C、D、
4. 已知双曲线上的一点P到一个焦点的距离为7，则P到另一个焦点的距离等于（ C ）
A．1或13 B．1 C．13 D．3
5．已知双曲线的一条渐近线方程为，则双曲线离心率（ ）
A． B． C． D．
6．设双曲线的虚轴长为2，焦距为，则其渐近线方程为（ ）
A．B．C．D．
7．已知双曲线的焦点为、，点在双曲线上且轴，则到直线的距离为( C )
(A) (B) (C) (D)
8．（多选题）曲线，则（ ）
A．C上的点满足，B．C关于x轴、y轴对称
C．C与x轴、y轴共有3个公共点D．C与直线只有1个公共点
【答案】ACD
【解析】
【分析】
去掉绝对值即可根据双曲线和椭圆的性质判断.
【详解】
表示椭圆在x轴上方的部分，
表示双曲线在x轴下方的部分，
作出图象：
双曲线的一条渐近线为，
故选项ACD正确，选项B错误.
故选：ACD.
二、填空题
9.（2016高考北京文数）已知双曲线 （，）的一条渐近线为，一个焦点为，则__1____；______2_______.
10．方程所表示的曲线为C，有下列命题：
①若曲线C为椭圆，则；
②若曲线C为双曲线，则或；
③曲线C不可能为圆；
④若曲线C表示焦点在上的双曲线，则.
以上命题正确的是 .（填上所有正确命题的序号）
三、解答题
11．根据下列条件，求双曲线的标准方程．
（1），，焦点在x轴上；
（2），经过点（－5，2），焦点在轴上．
（3）与双曲线有相同焦点，且经过点
（4）过点经过两点，且焦点在坐标轴上．
解：(1)由题设知，，，由，得.
因为双曲线的焦点在x轴上，所以所求双曲线的标准方程为；
（2）∵焦点在轴上，，
∴设所求双曲线方程为：（其中）
∵双曲线经过点（－5，2），∴
∴或（舍去）
∴所求双曲线方程是
（3）设所求双曲线方程为：
∵双曲线过点，∴
∴或（舍）
∴所求双曲线方程为
说明：（3）注意到了与双曲线有公共焦点的双曲线系方程为后，便有了以上巧妙的设法．
（4）【答案】
【解析】
【分析】
根据给定条件，设出双曲线方程，再利用待定系数法求解作答.
【详解】
设双曲线方程为，依题意有，解得，
所以所求双曲线的标准方程为：.
故答案为：
标准方程
图形


性质
焦点
，
，
焦距
范围
，
，
对称性
关于x轴、y轴和原点对称
顶点

轴
实轴长=，虚轴长=
离心率
渐近线方程