2024-2025学年江西省宜春市丰城九中八年级（上）开学数学试卷（A卷）（含答案）

这是一份2024-2025学年江西省宜春市丰城九中八年级（上）开学数学试卷（A卷）（含答案），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共6小题，每小题3分，共18分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下列图形中，是轴对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A. a2+a2=2a4B. (−3ab2)2=−6a2b4
C. a6÷(−a)2=a4D. (a−b)2=a2−b2
3.如果点P(2,b)和点Q(a,−3)关于直线x=1对称，则a+b的值是( )
A. −3B. 1C. −5D. 5
4.等腰三角形中有一内角等于80°，那么这个三角形的最小内角的度数为( )
A. 50B. 20C. 40或50D. 20或50
5.已知(x−2023)2+(x−2025)2=4050，则(x−2024)2的值是( )
A. 1B. 2025C. 2024D. 2023
6.如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A6B6A7的边长为( )
A. 6B. 12C. 32D. 64
二、填空题：本题共6小题，每小题3分，共18分。
7.如果分式有意义2+3x2−3x，那么x的取值范围是______，如果分式x2−9x+3的值为零，那么x= ______，如果(x−8)0有意义，那么x ______．
8.如图1六边形的内角和∠1+∠2+∠3+∠4+∠5+∠6为m度，如图2六边形的内角和∠1+∠2+∠3+∠4+∠5+∠6为n度，则m−n=______．
9.勾股定理被誉为“几何明珠”.在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图所示，把一个边长分别为3，4，5的三角形和三个正方形放置在大长方形ABCD中，则该长方形中空白部分的面积为______．
10.若关于x的分式方程x−4x−1=mxx−1有正整数解，则整数m为______．
11.若x2−6x+1=0，则x2+1x2= ______．
12.一个三位正整数n=100a+10b+3(其中a、b都是正整数，1≤a≤9，1≤b≤9)，满足各数位上的数字互不相同.将n的任意两个数位上的数字对调后得到三个不同的新三位数，把这三个新三位数的和记为M(n).若M(n)=999，则a+b= ，符合条件的n的所有值的和是 ．
三、解答题：本题共11小题，共84分。解答应写出文字说明，证明过程或演算步骤。
13.(本小题6分)
某同学在进行多边形的内角和的计算时，求得的内角和为1125°.当发现错了之后，重新检查，发现是多加了一个内角.问：多加的这个内角的度数是多少？这个多边形是几边形？
14.(本小题6分)
如图，在△ABC中，BE是∠ABC的角平分线，AD⊥BE，垂足为D，求证：∠2=∠1+∠C．
15.(本小题6分)
如图，在平面直角坐标系中，△ABC的顶点坐标分别为A(−3,2)，B(−4,−3)，C(−2,−2)．
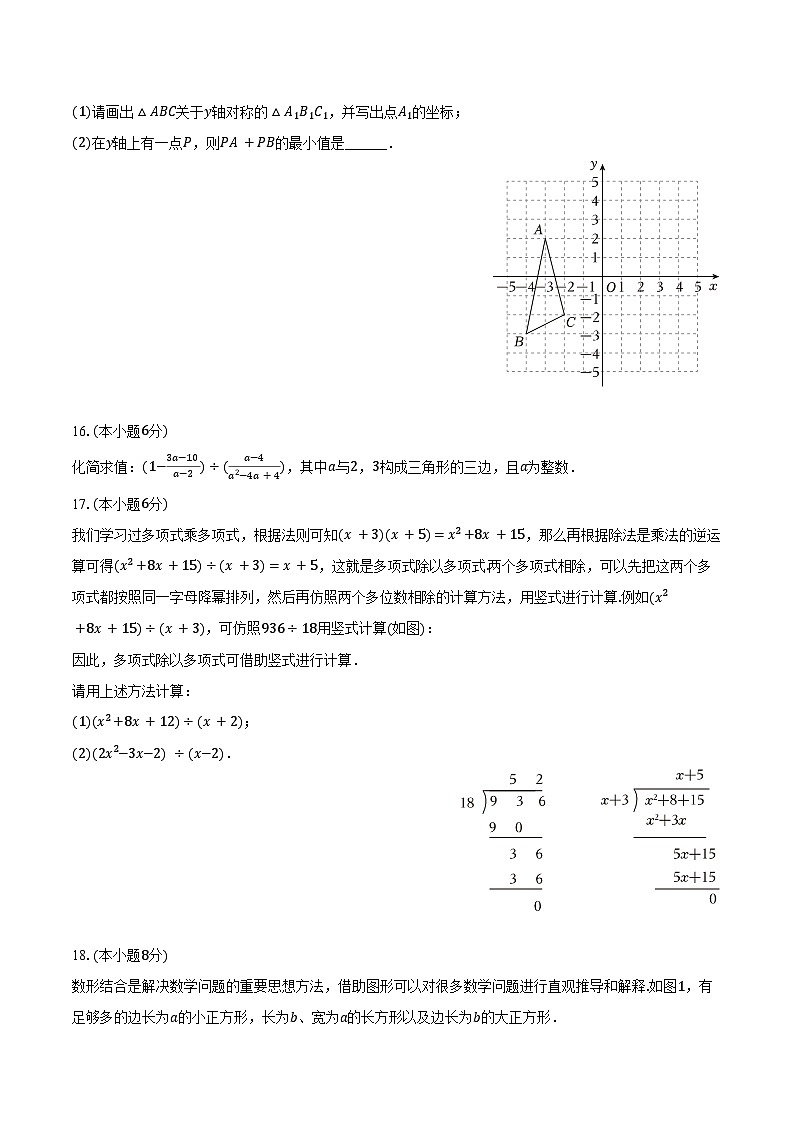
(1)请画出△ABC关于y轴对称的△A1B1C1，并写出点A1的坐标；
(2)在y轴上有一点P，则PA+PB的最小值是______．
16.(本小题6分)
化简求值：(1−3a−10a−2)÷(a−4a2−4a+4)，其中a与2，3构成三角形的三边，且a为整数．
17.(本小题6分)
我们学习过多项式乘多项式，根据法则可知(x+3)(x+5)=x2+8x+15，那么再根据除法是乘法的逆运算可得(x2+8x+15)÷(x+3)=x+5，这就是多项式除以多项式.两个多项式相除，可以先把这两个多项式都按照同一字母降幂排列，然后再仿照两个多位数相除的计算方法，用竖式进行计算.例如(x2+8x+15)÷(x+3)，可仿照936÷18用竖式计算(如图)：
因此，多项式除以多项式可借助竖式进行计算．
请用上述方法计算：
(1)(x2+8x+12)÷(x+2)；
(2)(2x2−3x−2)÷(x−2)．
18.(本小题8分)
数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释.如图1，有足够多的边长为a的小正方形，长为b、宽为a的长方形以及边长为b的大正方形．

利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式，例如图2可以解释整式乘法：(2a+b)(a+b)=2a2+3ab+b2，也可以解释因式分解：2a2+3ab+b2=(2a+b)(a+b)．
(1)若用4个B类材料围成图3的形状，设外围大正方形的边长为x，内部小正方形的边长为y，观察图案，指出下列关系式中正确的是(写出所有正确结论的序号) ______．
①a+b=x；②(x−y)2=2a2；③ab=x2−y24；④b2=a2+xy；⑤a2+b2=x2+y22．
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形，使其面积为3a2+5ab+2b2，在虚框中画出图形，并根据所画图形，将多项式3a2+5ab+2b2分解因式为______．
(3)若取其中的若干个(三种图形都要取到)拼成一个长方形，使其面积为4a2+mab+5b2，则m的值为______.(直接写出结果)
19.(本小题8分)
如图，在四边形ABCD中，∠BAD=α，∠BCD=180°−α，BD平分∠ABC．

(1)如图1，若α=90°，DA=2cm，则DC= ______；
(2)问题解决：如图2，求证：AD=CD；
(3)问题拓展：如图3，在等腰△ABC中，∠BAC=100°，BD平分∠ABC，求证：BD+AD=BC．
20.(本小题8分)
学校准备为运动会的某项活动购买A，B两种奖品，A中奖品的单价比B种商品的单价多2元，用600元购进A种奖品和用570元购进B种商品的数量相同．
(1)A种商品和B种商品的单价分别是多少？
(2)学校计划用不超过1555元的资金购进A、B两种奖品共40件，其中A种奖品的数量不低于B种奖品数量的一半，学校去购买的时候商店正在做促销活动，每件A种商品的售价优惠3元，B种商品的售价不变，请为学校设计出最省钱的购买方案．
21.(本小题9分)
教科书中这样写道：“我们把多项式a2+2ab+b2及a2−2ab+b2叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法.配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．
例如：分解因式x2+2x−3．
x2+2x−3
=(x2+2x+1)−4．
=(x+1)2−22
=(x+1+2)(x+1−2)
=(x+3)(x−1)
例如.求代数式2x2+4x−6的最小值．
原式=2x2+4x−6
=2(x2+2x−3)
=2(x+1)2−8．
可知当x=−1时，2x2+4x−6有最小值，最小值是−8．
(1)分解因式：a2−2a−3= ______．
(2)已知△ABC的三边长a、b、c都是整数，且满足a2+b2=4a+12b−40，求边长c的最小值；
(3)当x，y为何值时，多项式−x2+2xy−2y2+6y+7有最大值？并求出这个最大值．
22.(本小题9分)
(1)问题发现：如图①，△ABC和△EDC都是等边三角形，点B、D、E在同一条直线上，连接AE．
①∠AEC的度数为______；
②线段AE、BD之间的数量关系为______；
(2)拓展探究：如图②，△ABC和△EDC都是等腰直角三角形、∠ACB=∠DCE=90°，点B、D、E在同一条直线上，CM为△EDC中DE边上的高，连接AE，试求∠AEB的度数及判断线段CM、AE、BM之间的数量关系，并说明理由；
(3)解决问题：如图③，△ABC和△EDC都是等腰三角形，∠ACB=∠DCE=36°，点B、D，E在同一条直线上，请直接写出∠EAB+∠ECB的度数．
23.(本小题12分)
在平面直角坐标系xOy中，我们称横、纵坐标都是整数的点为“整点”，若坐标系内两个“整点”A(p,q)，B(m,n)(m≤n)满足关于x的多项式x2+px+q能够因式分解为(x+m)(x+n)，则称点B是点A的分解点，例如A(5,4)，B(1,4)满足x2+5x+4=(x+1)(x+4)，所以B是A的“分解点”．
(1)在点A1(3,2)，A2(0,5)，A3(−3,0)，A4(9,0)中，请找出不存在的“分解点”的点______．
(2)点P(a,1)存在分解点，求代数式3−a2a−4÷(a+2−5a−2)的值．
(3)在P，Q都在纵轴y轴上，(P在Q的上方)，点M在横轴x轴上，且点P、Q、M都存在“分解点”，若△PQM面积为5，请直接写出点M的坐标．
参考答案
1.B
2.C
3.A
4.D
5.C
6.C
7.x≠23 3 ≠8
8.0
9.60
10.0或1
11.34
12.6；1332．
13.解：由题意可知：
多加的内角为1125°−(n−2)⋅180°．
1125∘−(n−2)⋅180∘>01125∘−(n−2)⋅180∘