吉林省实验中学2024-2025学年九年级上学期第一次月考数学试题(无答案)

这是一份吉林省实验中学2024-2025学年九年级上学期第一次月考数学试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8小题，每小题3分，共24分）
1．下列各点不在抛物线图象上的是（ ）
A．B．C．D．
2．将抛物线向左平移3个单位长度，再向下平移2个单位长度，得到抛物线的解析式是（ ）
A．B．C．D．
3．从标号分别为1，2，3，4，5的5张卡片中随机抽取1张．下列事件中，必然事件是（ ）
A．标号小于6B．标号大于6C．标号是奇数D．标号是3
4．如图，我市在建的新城段路基的横断面为梯形ABCD，，斜坡AD长为8米，坡角α为，斜坡BC的坡角β为，则斜坡BC的长为（ ）
A．6米B．米C．4米D．米
5．若点三点在抛物线的图象上，则的大小关系是（ ）
A．B．C．D．
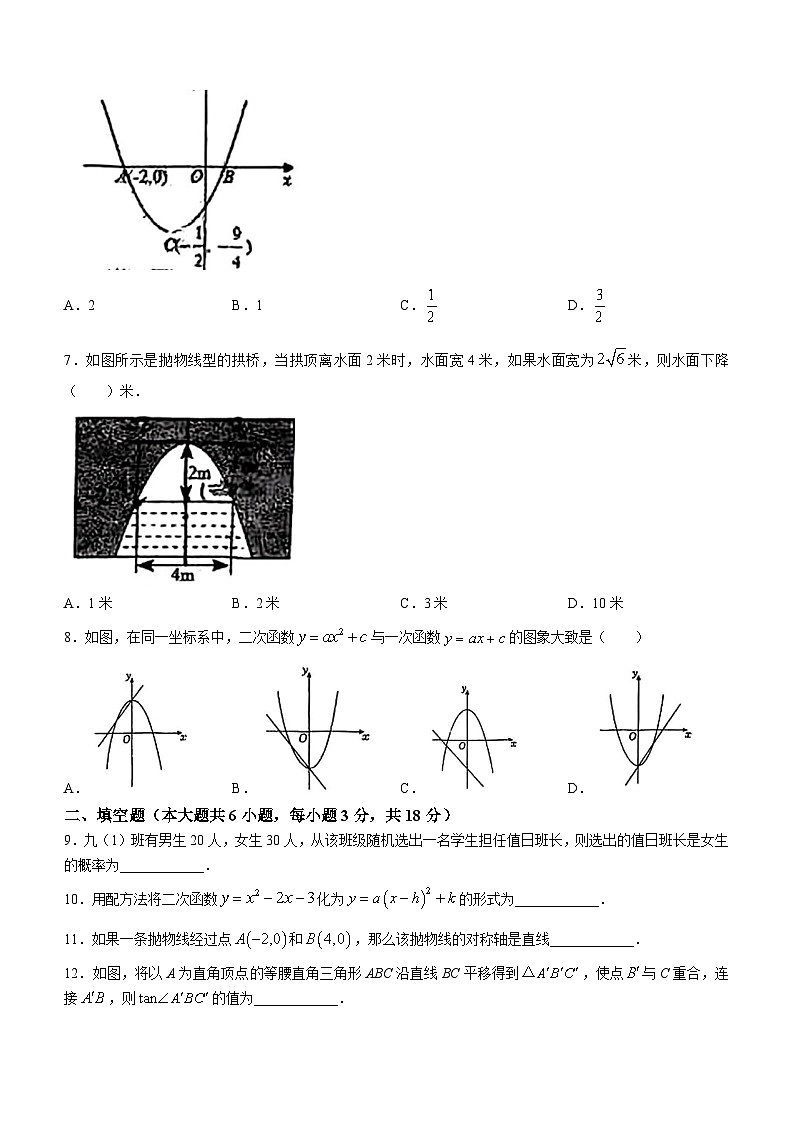
6．如图，二次函数图象与x轴交于A、B两点，顶点为C，其中点A、C坐标如图所示，则是一元二次方程的根是（ ）
A．2B．1C．D．
7．如图所示是抛物线型的拱桥，当拱顶离水面2米时，水面宽4米，如果水面宽为米，则水面下降（ ）米．
A．1米B．2米C．3米D．10米
8．如图，在同一坐标系中，二次函数与一次函数的图象大致是（ ）
A．B．C．D．
二、填空题（本大题共6小题，每小题3分，共18分）
9．九（1）班有男生20人，女生30人，从该班级随机选出一名学生担任值日班长，则选出的值日班长是女生的概率为____________．
10．用配方法将二次函数化为的形式为____________．
11．如果一条抛物线经过点和，那么该抛物线的对称轴是直线____________．
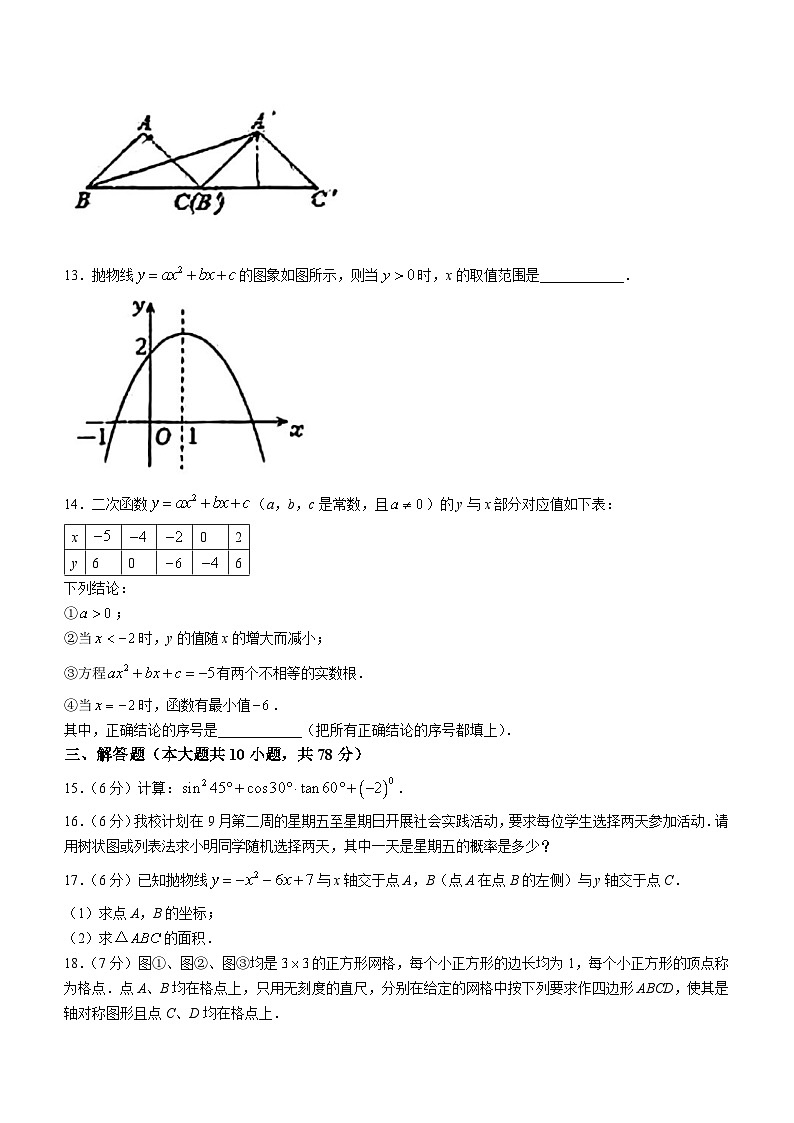
12．如图，将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到，使点与C重合，连接，则的值为____________．
13．抛物线的图象如图所示，则当时，x的取值范围是____________．
14．二次函数（a，b，c是常数，且）的y与x部分对应值如下表：
下列结论：
①；
②当时，y的值随x的增大而减小；
③方程有两个不相等的实数根．
④当时，函数有最小值．
其中，正确结论的序号是____________（把所有正确结论的序号都填上）．
三、解答题（本大题共10小题，共78分）
15．（6分）计算：．
16．（6分）我校计划在9月第二周的星期五至星期日开展社会实践活动，要求每位学生选择两天参加活动．请用树状图或列表法求小明同学随机选择两天，其中一天是星期五的概率是多少？
17．（6分）已知抛物线与x轴交于点A，B（点A在点B的左侧）与y轴交于点C．
（1）求点A，B的坐标；
（2）求的面积．
18．（7分）图①、图②、图③均是的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点．点A、B均在格点上，只用无刻度的直尺，分别在给定的网格中按下列要求作四边形ABCD，使其是轴对称图形且点C、D均在格点上．
（1）在图①中，四边形ABCD面积为2；
（2）在图②中，四边形ABCD面积为3；
（3）在图③中，四边形ABCD面积为4．
19．（7分）抛物线经过点．
（1）求抛物线的顶点坐标；
（2）将抛物线沿y轴向下平移后，所得新抛物线与x轴交于A、B两点，如果．，求新抛物线的表达式．
20．（7分）行驶中的汽车刹车后，由于惯性的作用，还会继续向前滑行一段距离，这段距离称为“刹车距离”，刹车距离是分析交通事故的重要依据．在一条限速120km/h的高速公路上，甲、乙两车相向而行，发现情况不对，同时刹车，但还是相撞了．事后测得甲车的刹车距离为21m，乙车的刹车距离超过20m，但小于21m，根据两车车型查阅资料可知：甲车的车速与刹车距离之间有关系：；乙车的车速与刹车距离之间则有关系：．请从两车的速度方面分析相撞是因为谁超速了．
21．（8分）如图，抛物线与x轴正半轴交于点，以OA为边在x轴上方作正方形OABC，延长CB交抛物线于点D，再以BD为边向上作矩形BDEF，使．
（1）求a的值；
（2）求点F的坐标．
22．（9分）数学活动课上，老师组织数学小组的同学们以“正方形折叠”为主题开展数学活动．
图（1） 图（2） 图（3）
【动手实践】
（1）如图（1），已知正方形纸片ABCD，数学小组将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠使AD与AM重合，折痕为AF，易知点E、M、F共线，则____________°，EF、BE、DF三条线段的关系为____________；
【拓展应用】
（2）解决下面问题：
①如图（2）作于N，交AM于P，求证：；
②如图（3），数学小组在图（1）的基础上进行如下操作：将正方形纸片沿EF继续折叠，点C的对应点为点N，他们发现，当点E的位置不同时，点N的位置也不同，若点N恰好落在边上，，请直接写出此时BE的长度．
23．（10分）如图，在中，，动点P从点A出发，以每秒1个单位的速度沿折线向终点B匀速运动．当点P不与A、B重合时，过P作于D，以PD、DB为邻边作矩形PDBF，设点P运动的时间是t（秒）．
（1）线段AB的长为____________；
（2）当矩形PDBF恰好是正方形时，求t的值；
（3）当时，求t的值：
（4）延长PD到点Q，使，连结FQ．当直线QF分矩形PDBF的面积为1∶5两部分时，直接写出t的值．
24．（12分）如图，抛物线经过点，抛物线与x轴的另一交点为点E，点P为抛物线上一动点，设点P的横坐标为m．
（1）求抛物线的解析式；
（2）若点P在第一象限，点M为抛物线对称轴上一点，当四边形MBEP恰好是平行四边形时，求点P的坐标；
（3）若点P在第四象限，连结PA、PE及AE，当t为何值时，的面积最大？最大面积是多少？
（4）是否存在点P，使为以AE为直角边的直角三角形，若存在，直接写出点P的坐标；若不存在，请说明理由． x
0
2
y
6
0
6